Question Number 108841 by 150505R last updated on 19/Aug/20
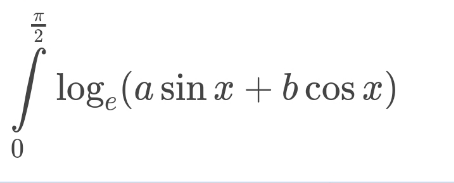
Answered by mathmax by abdo last updated on 19/Aug/20
![let take a try I =∫_0 ^(π/2) ln(asinx +bcosx)dx ⇒ I =∫_0 ^(π/2) ln(asinx)dx+∫_0 ^(π/2) ln(1+((bcosx)/(asinx)))dx (we suppose a≠0) ⇒ I =(π/2)lna −(π/2)ln(2) + ∫_0 ^(π/2) ln(1+(b/a)tanx)dx let for λ>0 f(λ) =∫_0 ^(π/2) ln(1+λtanx)dx ⇒f^′ (λ) =∫_0 ^(π/2) ((tanx)/(1+λtanx))dx =_(tanx =t) ∫_0 ^∞ (t/((1+λt)))(dt/(1+t^2 )) let decompose F(t) =(t/((λt+1)(t^2 +1))) ⇒F(t) =(α/(λt +1)) +((et +f)/(t^2 +1)) α =((−1)/(λ((1/λ^2 )+1))) =((−1)/((1/λ) +λ)) =((−λ)/(1+λ^2 )) lim_(t→+∞) tF(t) =0 =(α/λ) +e ⇒e =−(α/λ) =(1/(1+λ^2 )) F(o) =o =α +f ⇒f =(λ/(1+λ^2 )) ⇒F(t) =((−λ)/((1+λ^2 )(λt+1)))+(((1/(1+λ^2 ))t+(λ/(1+λ^2 )))/(t^2 +1)) ⇒f^′ (λ) =(1/(1+λ^2 )){ −λ ∫_0 ^∞ (dt/(λt +1)) +(1/2)∫_0 ^∞ ((2t)/(t^2 +1))dt +λ ∫_0 ^∞ (dt/(t^2 +1))} =(1/(1+λ^2 )){ [ln∣((√(t^2 +1))/(λt +1))∣]_0 ^∞ +((λπ)/2)} =(1/(1+λ^2 ))(−lnλ) +(π/2) .(λ/(1+λ^2 )) ⇒ f(λ) =−∫_0 ^λ ((lnt)/(1+t^2 ))dt +(π/2)∫_0 ^λ (t/(1+t^2 ))dt +C =(π/4)ln(1+λ^2 )−∫_0 ^λ ((ln(t))/(1+t^2 ))dt +C we have C=f(0)=0 ⇒ f(λ) =(π/4)ln(1+λ^2 )−∫_0 ^λ ((ln(t))/(1+t^2 ))dt ⇒f((b/a)) =(π/4)ln(1+(b^2 /a^2 ))−∫_0 ^(b/a) ((lnt)/(1+t^2 ))dt ⇒ I =(π/2)ln((a/2)) +(π/4)ln(1+(b^2 /a^2 )) −∫_0 ^(b/a) ((lnt)/(1+t^2 ))dt ...be continued...](https://www.tinkutara.com/question/Q108881.png)
$$\mathrm{let}\:\mathrm{take}\:\mathrm{a}\:\mathrm{try}\:\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{asinx}\:+\mathrm{bcosx}\right)\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{asinx}\right)\mathrm{dx}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{bcosx}}{\mathrm{asinx}}\right)\mathrm{dx}\:\:\:\:\:\:\left(\mathrm{we}\:\mathrm{suppose}\:\mathrm{a}\neq\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\pi}{\mathrm{2}}\mathrm{lna}\:−\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)\:+\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{b}}{\mathrm{a}}\mathrm{tanx}\right)\mathrm{dx}\:\mathrm{let}\:\mathrm{for}\:\lambda>\mathrm{0} \\ $$$$\mathrm{f}\left(\lambda\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{1}+\lambda\mathrm{tanx}\right)\mathrm{dx}\:\Rightarrow\mathrm{f}^{'} \left(\lambda\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{tanx}}{\mathrm{1}+\lambda\mathrm{tanx}}\mathrm{dx} \\ $$$$=_{\mathrm{tanx}\:=\mathrm{t}} \:\:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{t}}{\left(\mathrm{1}+\lambda\mathrm{t}\right)}\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:\:\mathrm{let}\:\mathrm{decompose} \\ $$$$\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{t}}{\left(\lambda\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\alpha}{\lambda\mathrm{t}\:+\mathrm{1}}\:+\frac{\mathrm{et}\:+\mathrm{f}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\alpha\:=\frac{−\mathrm{1}}{\lambda\left(\frac{\mathrm{1}}{\lambda^{\mathrm{2}} }+\mathrm{1}\right)}\:=\frac{−\mathrm{1}}{\frac{\mathrm{1}}{\lambda}\:+\lambda}\:=\frac{−\lambda}{\mathrm{1}+\lambda^{\mathrm{2}} } \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)\:=\mathrm{0}\:=\frac{\alpha}{\lambda}\:+\mathrm{e}\:\Rightarrow\mathrm{e}\:=−\frac{\alpha}{\lambda}\:=\frac{\mathrm{1}}{\mathrm{1}+\lambda^{\mathrm{2}} } \\ $$$$\mathrm{F}\left(\mathrm{o}\right)\:=\mathrm{o}\:=\alpha\:+\mathrm{f}\:\Rightarrow\mathrm{f}\:=\frac{\lambda}{\mathrm{1}+\lambda^{\mathrm{2}} }\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)\:=\frac{−\lambda}{\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)\left(\lambda\mathrm{t}+\mathrm{1}\right)}+\frac{\frac{\mathrm{1}}{\mathrm{1}+\lambda^{\mathrm{2}} }\mathrm{t}+\frac{\lambda}{\mathrm{1}+\lambda^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\lambda\right)\:=\frac{\mathrm{1}}{\mathrm{1}+\lambda^{\mathrm{2}} }\left\{\:−\lambda\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\lambda\mathrm{t}\:+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:+\lambda\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+\lambda^{\mathrm{2}} }\left\{\:\left[\mathrm{ln}\mid\frac{\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}}{\lambda\mathrm{t}\:+\mathrm{1}}\mid\right]_{\mathrm{0}} ^{\infty} \:+\frac{\lambda\pi}{\mathrm{2}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+\lambda^{\mathrm{2}} }\left(−\mathrm{ln}\lambda\right)\:+\frac{\pi}{\mathrm{2}}\:.\frac{\lambda}{\mathrm{1}+\lambda^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{f}\left(\lambda\right)\:=−\int_{\mathrm{0}} ^{\lambda} \:\frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\:+\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\lambda} \:\frac{\mathrm{t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:+\mathrm{C} \\ $$$$=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)−\int_{\mathrm{0}} ^{\lambda} \:\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:+\mathrm{C}\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{C}=\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{f}\left(\lambda\right)\:=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)−\int_{\mathrm{0}} ^{\lambda} \:\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\Rightarrow\mathrm{f}\left(\frac{\mathrm{b}}{\mathrm{a}}\right)\:=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }\right)−\int_{\mathrm{0}} ^{\frac{\mathrm{b}}{\mathrm{a}}} \:\frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\Rightarrow\:\mathrm{I}\:=\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{a}}{\mathrm{2}}\right)\:+\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }\right)\:−\int_{\mathrm{0}} ^{\frac{\mathrm{b}}{\mathrm{a}}} \:\frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$…\mathrm{be}\:\mathrm{continued}… \\ $$
