Question Number 108868 by ajfour last updated on 19/Aug/20
Commented by ajfour last updated on 19/Aug/20

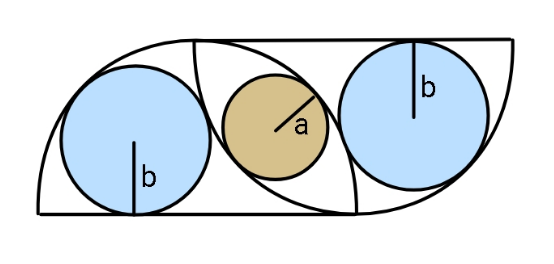
$${Find}\:{b}/{a}. \\ $$
Answered by ajfour last updated on 19/Aug/20
Commented by ajfour last updated on 19/Aug/20

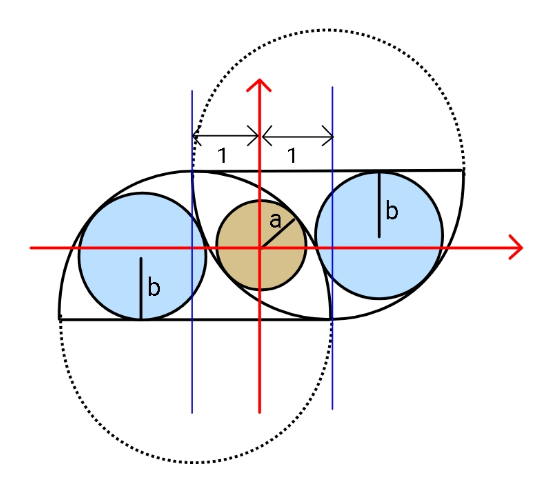
$${Let}\:{Eq}.\:{of}\:{left}\:{semicircle}\:{is} \\ $$$$\:\:\:\:\:\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\left({y}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4} \\ $$$${Its}\:{intersection}\:{with}\:\:{y}={x}\:{line} \\ $$$${gives}\:\:\:\left(\frac{{a}}{\:\sqrt{\mathrm{2}}}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2} \\ $$$$\Rightarrow\:\:\:\:\:{a}=\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\:=\:\mathrm{2}−\sqrt{\mathrm{2}} \\ $$$${let}\:{center}\:{of}\:{right}\:{blue}\:{circle}\:{be} \\ $$$${C}\left({h},\:{k}\right)\:\:\:\:\&\:\:\:{k}=\mathrm{1}−{b} \\ $$$$\Rightarrow\:\:\:\left({h}+\mathrm{1}\right)^{\mathrm{2}} +\left({k}+\mathrm{1}\right)^{\mathrm{2}} =\left({b}+\mathrm{2}\right)^{\mathrm{2}} \:\:\:\:\& \\ $$$$\:\:\:\:\:\:\:\:\:\left({h}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{1}−{k}\right)^{\mathrm{2}} =\left(\mathrm{2}−{b}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\left({h}+\mathrm{1}\right)^{\mathrm{2}} =\:\mathrm{8}{b} \\ $$$$\:\:\:\:\:\:\:\:\:\left({h}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}−\mathrm{4}{b} \\ $$$$\Rightarrow\:\:\:\mathrm{4}{h}=\mathrm{12}{b}−\mathrm{4}\:\:\:\Rightarrow\:\:{h}=\mathrm{3}{b}−\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:\:\mathrm{9}{b}^{\mathrm{2}} =\mathrm{8}{b}\:\:\:\:\Rightarrow\:\:\:{b}=\frac{\mathrm{8}}{\mathrm{9}} \\ $$$$\:{hence}\:\:\frac{{b}}{{a}}=\frac{\mathrm{8}}{\mathrm{9}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)}\:=\:\frac{\mathrm{4}}{\mathrm{9}}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\:. \\ $$
Answered by mr W last updated on 19/Aug/20
Commented by mr W last updated on 19/Aug/20
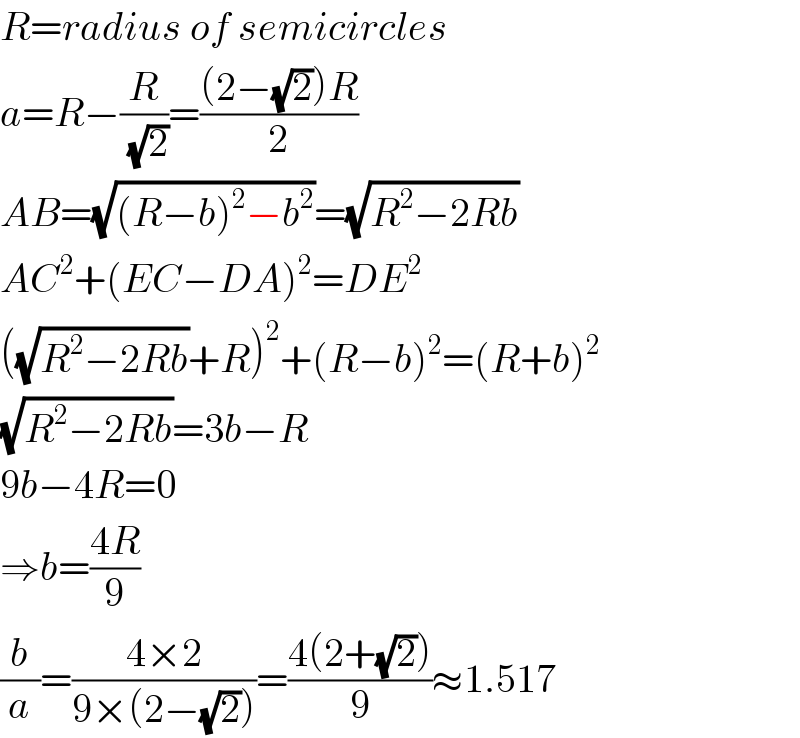
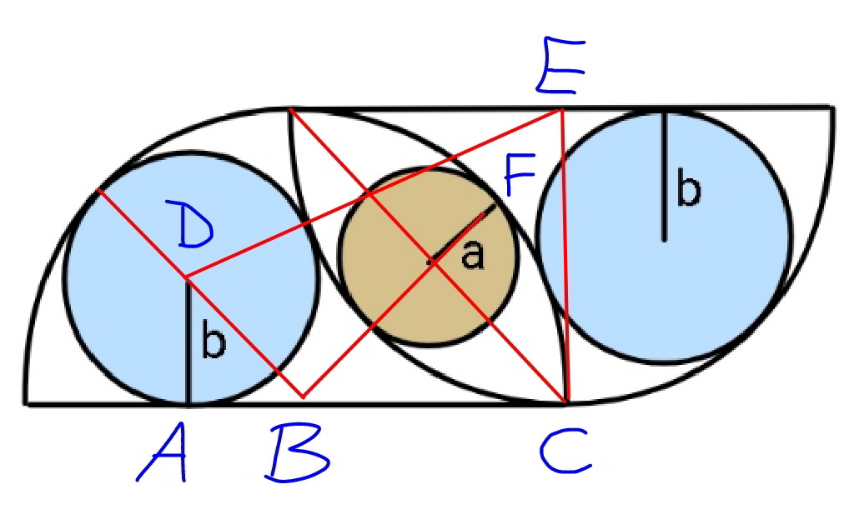
$${R}={radius}\:{of}\:{semicircles} \\ $$$${a}={R}−\frac{{R}}{\:\sqrt{\mathrm{2}}}=\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right){R}}{\mathrm{2}} \\ $$$${AB}=\sqrt{\left({R}−{b}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} }=\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Rb}} \\ $$$${AC}^{\mathrm{2}} +\left({EC}−{DA}\right)^{\mathrm{2}} ={DE}^{\mathrm{2}} \\ $$$$\left(\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Rb}}+{R}\right)^{\mathrm{2}} +\left({R}−{b}\right)^{\mathrm{2}} =\left({R}+{b}\right)^{\mathrm{2}} \\ $$$$\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Rb}}=\mathrm{3}{b}−{R} \\ $$$$\mathrm{9}{b}−\mathrm{4}{R}=\mathrm{0} \\ $$$$\Rightarrow{b}=\frac{\mathrm{4}{R}}{\mathrm{9}} \\ $$$$\frac{{b}}{{a}}=\frac{\mathrm{4}×\mathrm{2}}{\mathrm{9}×\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)}=\frac{\mathrm{4}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)}{\mathrm{9}}\approx\mathrm{1}.\mathrm{517} \\ $$
Commented by ajfour last updated on 19/Aug/20

$${Understood}\:{Sir},\:{your}\:{way}\:{is} \\ $$$${simpler},\:{thanks}\:{a}\:{lot}! \\ $$
