Question Number 108931 by mohammad17 last updated on 20/Aug/20

Commented by mohammad17 last updated on 20/Aug/20
$${sir}\:{can}\:{you}\:{help}\:{me}\:{pleas} \\ $$
Answered by Aziztisffola last updated on 20/Aug/20

$$\:\mathrm{let}\:\mathrm{A}\left(\mathrm{1};\mathrm{2};\mathrm{3}\right)\:\mathrm{and}\:\left(\bigtriangleup\right)\begin{cases}{{x}=\mathrm{2}+\mathrm{2}{t}}\\{{y}=\mathrm{1}+\mathrm{6}{t}}\\{{z}=\mathrm{3}}\end{cases}\Rightarrow\overset{\rightarrow} {{u}}\begin{pmatrix}{\mathrm{2}}\\{\mathrm{6}}\\{\mathrm{0}}\end{pmatrix}\:\: \\ $$$$\:\mathrm{B}\left({x}_{\mathrm{0}} ;{y}_{\mathrm{0}} ;{z}_{\mathrm{0}} \right)\in\left(\bigtriangleup\right)\:\mathrm{such}\:\mathrm{that}\:\left(\mathrm{AB}\right)\bot\left(\bigtriangleup\right)\: \\ $$$$\:\overset{\rightarrow} {\mathrm{AB}}\begin{pmatrix}{{x}_{\mathrm{0}} −\mathrm{1}}\\{{y}_{\mathrm{0}} −\mathrm{2}}\\{{z}_{\mathrm{0}} −\mathrm{3}}\end{pmatrix}\:\:\overset{\rightarrow} {\:\mathrm{AB}}.\overset{\rightarrow} {{u}}=\mathrm{0} \\ $$$$\:\mathrm{2}{x}_{\mathrm{0}} −\mathrm{2}+\mathrm{6}{y}_{\mathrm{0}} −\mathrm{12}=\mathrm{0} \\ $$$$\:{x}_{\mathrm{0}} +\mathrm{3}{y}_{\mathrm{0}} −\mathrm{7}=\mathrm{0} \\ $$$$\:\mathrm{we}\:\mathrm{know}\:\mathrm{B}\left({x}_{\mathrm{0}} ;{y}_{\mathrm{0}} ;{z}_{\mathrm{0}} \right)\in\left(\bigtriangleup\right) \\ $$$$\Rightarrow\:\begin{cases}{{x}_{\mathrm{0}} =\mathrm{2}+\mathrm{2}{t}}\\{{y}_{\mathrm{0}} =\mathrm{1}+\mathrm{6}{t}}\\{{z}_{\mathrm{0}} =\mathrm{3}}\end{cases}\Rightarrow\mathrm{2}+\mathrm{2}{t}+\mathrm{3}\left(\mathrm{1}+\mathrm{6}{t}\right)−\mathrm{7}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{20}{t}=\mathrm{2}\Rightarrow{t}=\mathrm{0}.\mathrm{1} \\ $$$$\:\mathrm{then}\:\mathrm{B}\left(\mathrm{2}.\mathrm{2};\mathrm{1}.\mathrm{6};\mathrm{3}\right) \\ $$$$\:\mathrm{Hence}\:\overset{\rightarrow} {\mathrm{AB}}\begin{pmatrix}{\mathrm{2}.\mathrm{2}−\mathrm{1}}\\{\mathrm{1}.\mathrm{6}−\mathrm{2}}\\{\mathrm{3}−\mathrm{3}}\end{pmatrix}\:\Leftrightarrow\overset{\rightarrow} {\mathrm{AB}}\begin{pmatrix}{\mathrm{1}.\mathrm{2}}\\{−\mathrm{0}.\mathrm{4}}\\{\mathrm{0}}\end{pmatrix}\:\: \\ $$$$\mathrm{d}\left(\mathrm{A};\left(\bigtriangleup\right)\right)=\mathrm{AB}=\sqrt{\left(\mathrm{1}.\mathrm{2}\right)^{\mathrm{2}} +\left(−\mathrm{0}.\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}.\mathrm{36} \\ $$
Answered by Aziztisffola last updated on 20/Aug/20
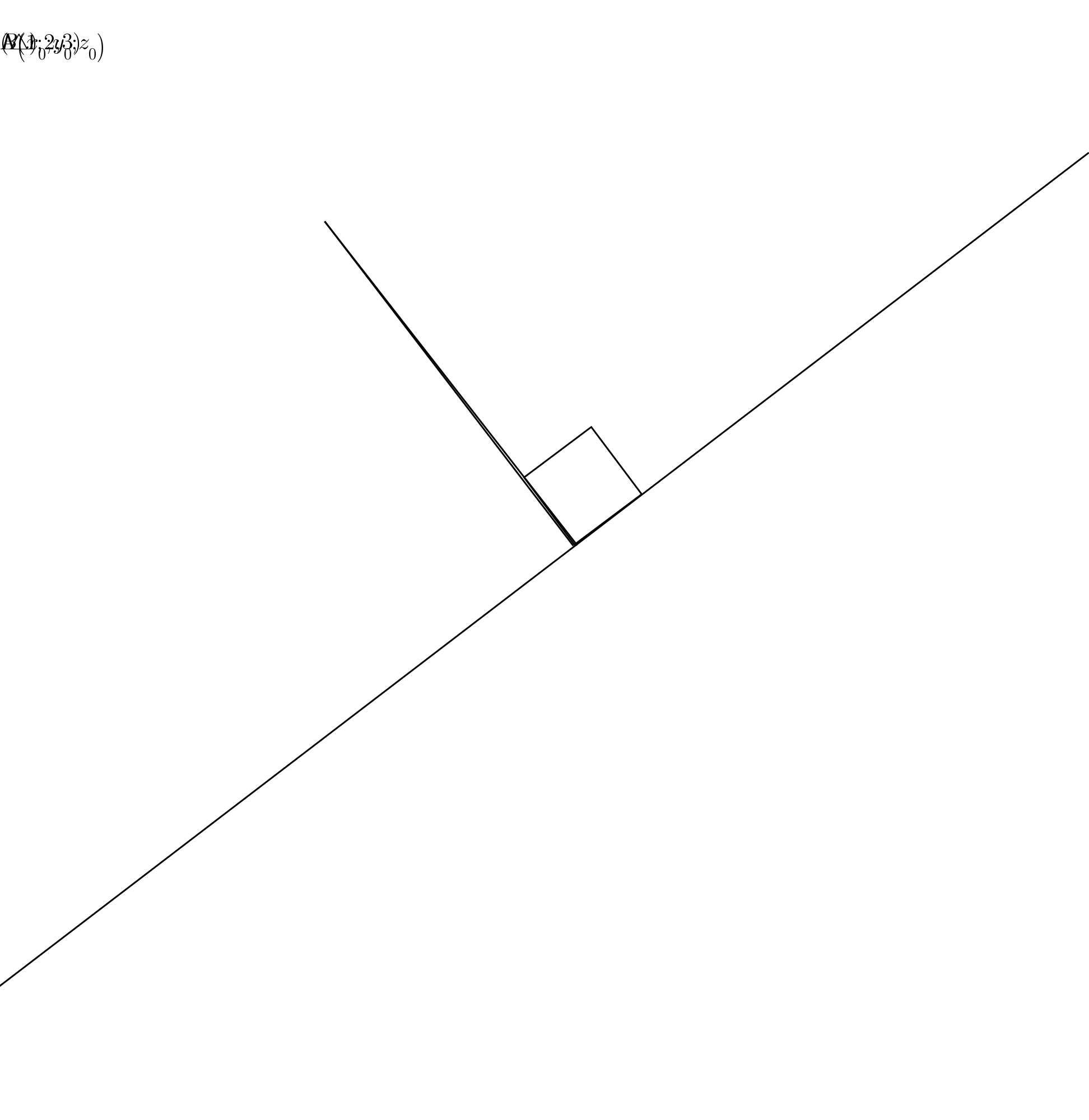
$$ \\ $$$$ \\ $$
