Question Number 109067 by n0y0n last updated on 20/Aug/20

Answered by Aziztisffola last updated on 20/Aug/20
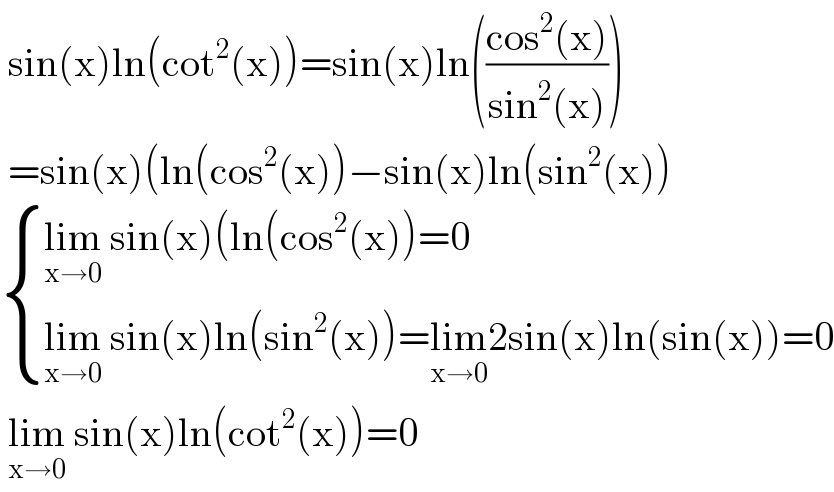
$$\:\mathrm{sin}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{cot}^{\mathrm{2}} \left(\mathrm{x}\right)\right)=\mathrm{sin}\left(\mathrm{x}\right)\mathrm{ln}\left(\frac{\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)}\right) \\ $$$$\:=\mathrm{sin}\left(\mathrm{x}\right)\left(\mathrm{ln}\left(\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)\right)−\mathrm{sin}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\right)\right. \\ $$$$\begin{cases}{\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{sin}\left(\mathrm{x}\right)\left(\mathrm{ln}\left(\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)\right)=\mathrm{0}\right.}\\{\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{sin}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\right)=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}2sin}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{sin}\left(\mathrm{x}\right)\right)=\mathrm{0}}\end{cases} \\ $$$$\:\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{sin}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{cot}^{\mathrm{2}} \left(\mathrm{x}\right)\right)=\mathrm{0} \\ $$
