Question-109070

Question Number 109070 by Aziztisffola last updated on 20/Aug/20

Commented by kaivan.ahmadi last updated on 21/Aug/20

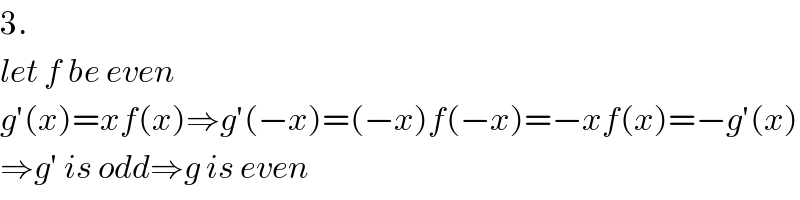
3. let f be even g′(x)=xf(x)⇒g′(−x)=(−x)f(−x)=−xf(x)=−g′(x) ⇒g′ is odd⇒g is even

$$\mathrm{3}. \\ $$$${let}\:{f}\:{be}\:{even} \\ $$$${g}'\left({x}\right)={xf}\left({x}\right)\Rightarrow{g}'\left(−{x}\right)=\left(−{x}\right){f}\left(−{x}\right)=−{xf}\left({x}\right)=−{g}'\left({x}\right) \\ $$$$\Rightarrow{g}'\:{is}\:{odd}\Rightarrow{g}\:{is}\:{even} \\ $$

Commented by Aziztisffola last updated on 21/Aug/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by kaivan.ahmadi last updated on 21/Aug/20

$$\mathrm{1}. \\ $$$${g}'\left({x}\right)={xf}\left({x}\right) \\ $$$${g}'\:{is}\:{defined}\:{on}\:{R} \\ $$

Commented by Aziztisffola last updated on 21/Aug/20

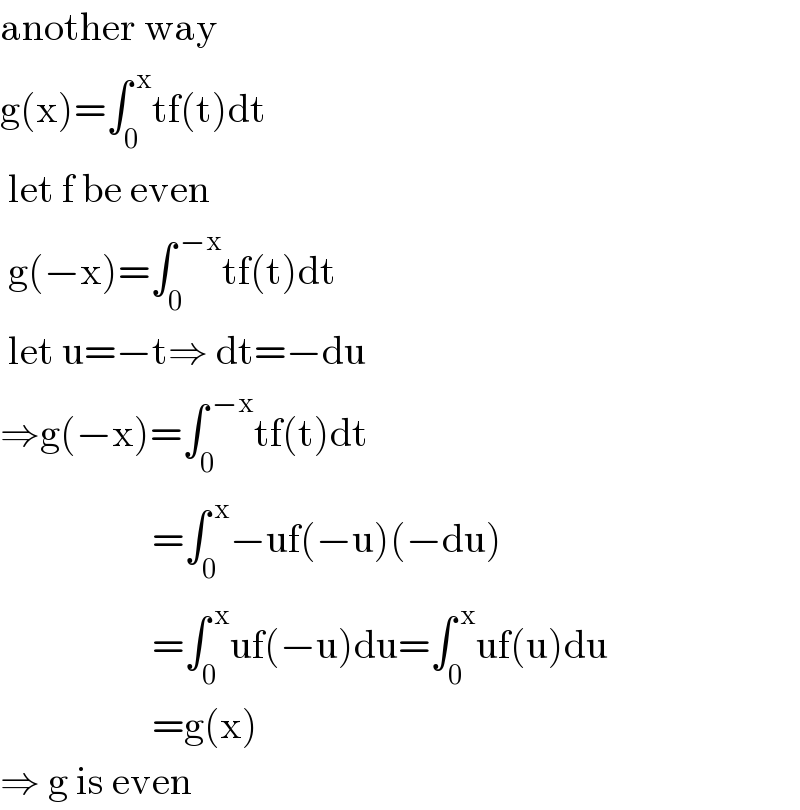
another way g(x)=∫_0 ^( x) tf(t)dt let f be even g(−x)=∫_0 ^( −x) tf(t)dt let u=−t⇒ dt=−du ⇒g(−x)=∫_0 ^( −x) tf(t)dt =∫_0 ^( x) −uf(−u)(−du) =∫_0 ^( x) uf(−u)du=∫_0 ^( x) uf(u)du =g(x) ⇒ g is even

$$\mathrm{another}\:\mathrm{way} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\:\mathrm{x}} \mathrm{tf}\left(\mathrm{t}\right)\mathrm{dt}\: \\ $$$$\:\mathrm{let}\:\mathrm{f}\:\mathrm{be}\:\mathrm{even} \\ $$$$\:\mathrm{g}\left(−\mathrm{x}\right)=\int_{\mathrm{0}} ^{\:−\mathrm{x}} \mathrm{tf}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$\:\mathrm{let}\:\mathrm{u}=−\mathrm{t}\Rightarrow\:\mathrm{dt}=−\mathrm{du} \\ $$$$\Rightarrow\mathrm{g}\left(−\mathrm{x}\right)=\int_{\mathrm{0}} ^{\:−\mathrm{x}} \mathrm{tf}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\:\mathrm{x}} −\mathrm{uf}\left(−\mathrm{u}\right)\left(−\mathrm{du}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\:\mathrm{x}} \mathrm{uf}\left(−\mathrm{u}\right)\mathrm{du}=\int_{\mathrm{0}} ^{\:\mathrm{x}} \mathrm{uf}\left(\mathrm{u}\right)\mathrm{du} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{g}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\:\mathrm{g}\:\mathrm{is}\:\mathrm{even} \\ $$

Commented by kaivan.ahmadi last updated on 21/Aug/20

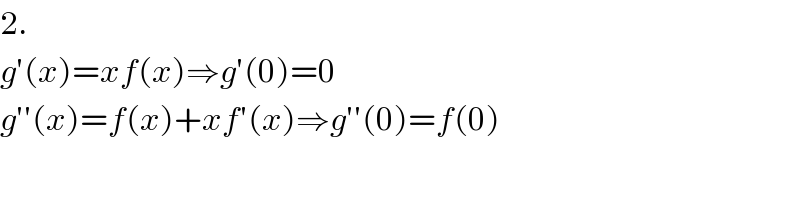
2. g′(x)=xf(x)⇒g′(0)=0 g′′(x)=f(x)+xf′(x)⇒g′′(0)=f(0)

$$\mathrm{2}. \\ $$$${g}'\left({x}\right)={xf}\left({x}\right)\Rightarrow{g}'\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${g}''\left({x}\right)={f}\left({x}\right)+{xf}'\left({x}\right)\Rightarrow{g}''\left(\mathrm{0}\right)={f}\left(\mathrm{0}\right) \\ $$$$ \\ $$

Commented by kaivan.ahmadi last updated on 21/Aug/20

$${beautiful}\:{stright}\:{proof}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply