Question Number 109167 by Dwaipayan Shikari last updated on 21/Aug/20

Answered by mr W last updated on 21/Aug/20
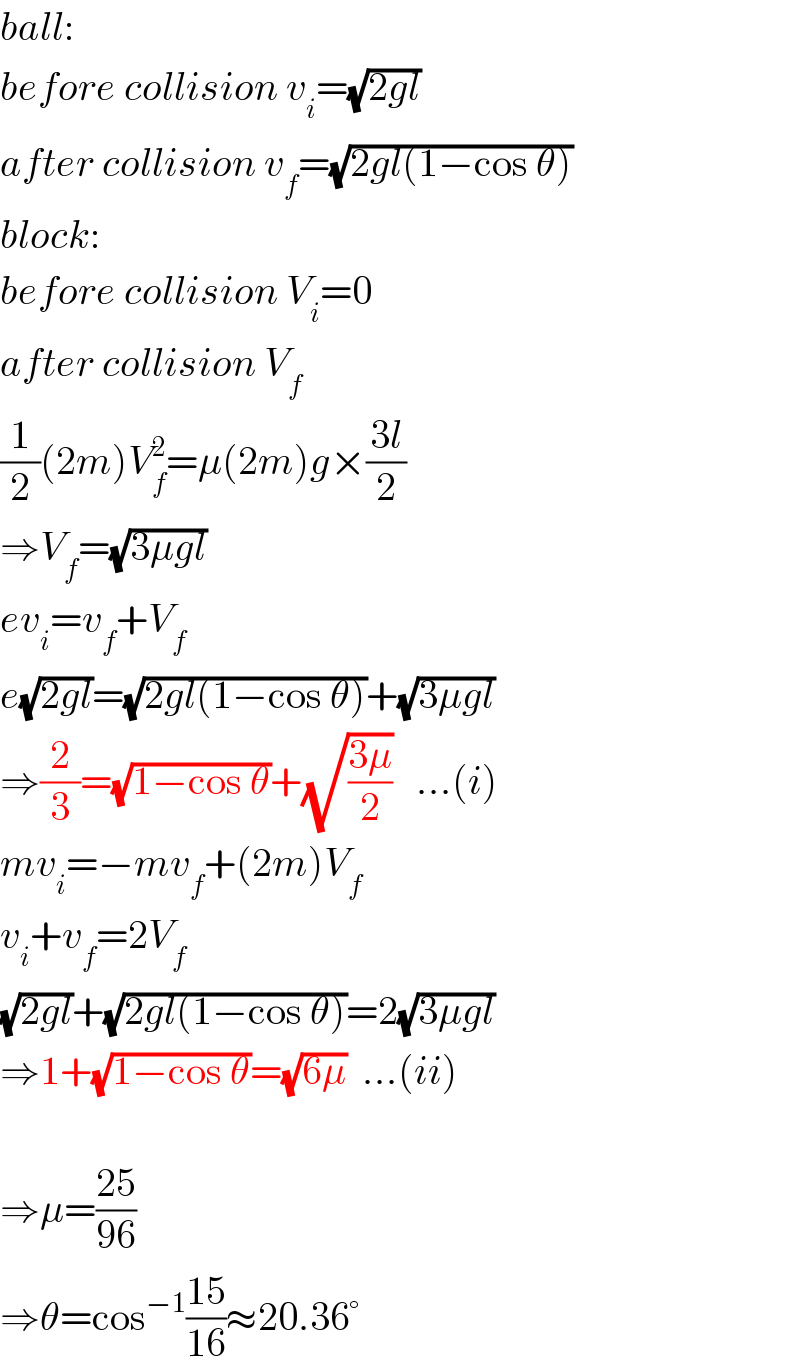
$${ball}: \\ $$$${before}\:{collision}\:{v}_{{i}} =\sqrt{\mathrm{2}{gl}} \\ $$$${after}\:{collision}\:{v}_{{f}} =\sqrt{\mathrm{2}{gl}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)} \\ $$$${block}: \\ $$$${before}\:{collision}\:{V}_{{i}} =\mathrm{0} \\ $$$${after}\:{collision}\:{V}_{{f}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{m}\right){V}_{{f}} ^{\mathrm{2}} =\mu\left(\mathrm{2}{m}\right){g}×\frac{\mathrm{3}{l}}{\mathrm{2}} \\ $$$$\Rightarrow{V}_{{f}} =\sqrt{\mathrm{3}\mu{gl}} \\ $$$${ev}_{{i}} ={v}_{{f}} +{V}_{{f}} \\ $$$${e}\sqrt{\mathrm{2}{gl}}=\sqrt{\mathrm{2}{gl}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}+\sqrt{\mathrm{3}\mu{gl}} \\ $$$$\Rightarrow\frac{\mathrm{2}}{\mathrm{3}}=\sqrt{\mathrm{1}−\mathrm{cos}\:\theta}+\sqrt{\frac{\mathrm{3}\mu}{\mathrm{2}}}\:\:\:…\left({i}\right) \\ $$$${mv}_{{i}} =−{mv}_{{f}} +\left(\mathrm{2}{m}\right){V}_{{f}} \\ $$$${v}_{{i}} +{v}_{{f}} =\mathrm{2}{V}_{{f}} \\ $$$$\sqrt{\mathrm{2}{gl}}+\sqrt{\mathrm{2}{gl}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}=\mathrm{2}\sqrt{\mathrm{3}\mu{gl}} \\ $$$$\Rightarrow\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{cos}\:\theta}=\sqrt{\mathrm{6}\mu}\:\:…\left({ii}\right) \\ $$$$ \\ $$$$\Rightarrow\mu=\frac{\mathrm{25}}{\mathrm{96}} \\ $$$$\Rightarrow\theta=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{15}}{\mathrm{16}}\approx\mathrm{20}.\mathrm{36}° \\ $$
