Menu Close

Question-109246

Tinku Tara 0 Comments
Pin




Question Number 109246 by peter frank last updated on 22/Aug/20
Answered by Ar Brandon last updated on 22/Aug/20
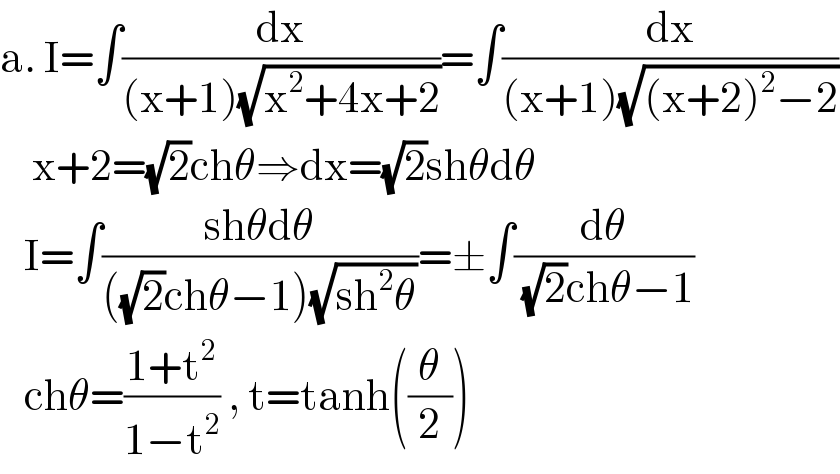
a. I=∫(dx/((x+1)(√(x^2 +4x+2))))=∫(dx/((x+1)(√((x+2)^2 −2)))) x+2=(√2)chθ⇒dx=(√2)shθdθ I=∫((shθdθ)/(((√2)chθ−1)(√(sh^2 θ))))=±∫(dθ/( (√2)chθ−1)) chθ=((1+t^2 )/(1−t^2 )) , t=tanh((θ/2))
$$\mathrm{a}.\:\mathrm{I}=\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{2}}}=\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}}} \\ $$$$\:\:\:\:\mathrm{x}+\mathrm{2}=\sqrt{\mathrm{2}}\mathrm{ch}\theta\Rightarrow\mathrm{dx}=\sqrt{\mathrm{2}}\mathrm{sh}\theta\mathrm{d}\theta \\ $$$$\:\:\:\mathrm{I}=\int\frac{\mathrm{sh}\theta\mathrm{d}\theta}{\left(\sqrt{\mathrm{2}}\mathrm{ch}\theta−\mathrm{1}\right)\sqrt{\mathrm{sh}^{\mathrm{2}} \theta}}=\pm\int\frac{\mathrm{d}\theta}{\:\sqrt{\mathrm{2}}\mathrm{ch}\theta−\mathrm{1}} \\ $$$$\:\:\:\mathrm{ch}\theta=\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:,\:\mathrm{t}=\mathrm{tanh}\left(\frac{\theta}{\mathrm{2}}\right) \\ $$
Answered by Ar Brandon last updated on 22/Aug/20
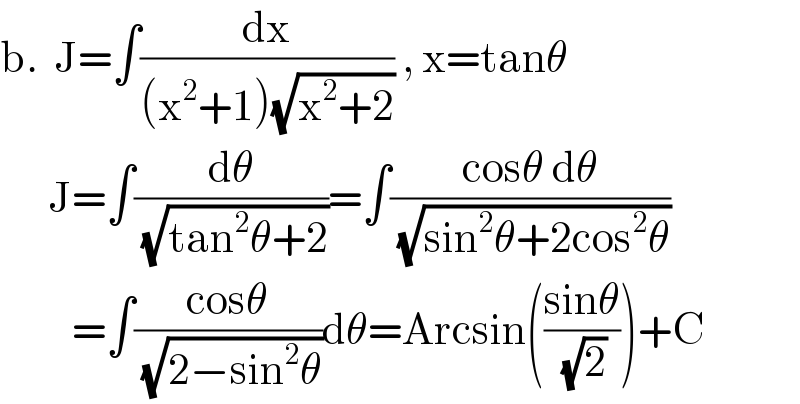
b. J=∫(dx/((x^2 +1)(√(x^2 +2)))) , x=tanθ J=∫(dθ/( (√(tan^2 θ+2))))=∫((cosθ dθ)/( (√(sin^2 θ+2cos^2 θ)))) =∫((cosθ)/( (√(2−sin^2 θ))))dθ=Arcsin(((sinθ)/( (√2))))+C
$$\mathrm{b}.\:\:\mathrm{J}=\int\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2}}}\:,\:\mathrm{x}=\mathrm{tan}\theta \\ $$$$\:\:\:\:\:\:\mathrm{J}=\int\frac{\mathrm{d}\theta}{\:\sqrt{\mathrm{tan}^{\mathrm{2}} \theta+\mathrm{2}}}=\int\frac{\mathrm{cos}\theta\:\mathrm{d}\theta}{\:\sqrt{\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{2cos}^{\mathrm{2}} \theta}} \\ $$$$\:\:\:\:\:\:\:\:\:=\int\frac{\mathrm{cos}\theta}{\:\sqrt{\mathrm{2}−\mathrm{sin}^{\mathrm{2}} \theta}}\mathrm{d}\theta=\mathrm{Arcsin}\left(\frac{\mathrm{sin}\theta}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{C} \\ $$
Answered by Ar Brandon last updated on 22/Aug/20
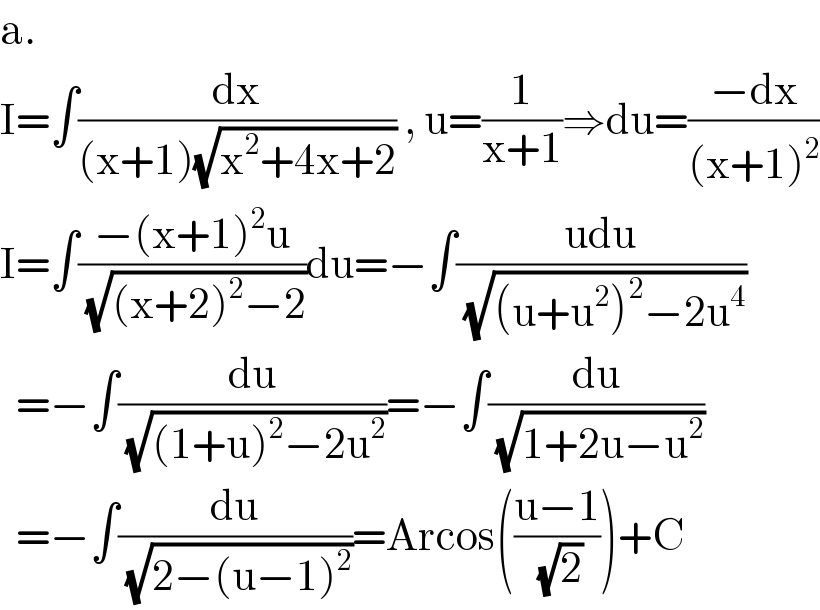
a. I=∫(dx/((x+1)(√(x^2 +4x+2)))) , u=(1/(x+1))⇒du=((−dx)/((x+1)^2 )) I=∫((−(x+1)^2 u)/( (√((x+2)^2 −2))))du=−∫((udu)/( (√((u+u^2 )^2 −2u^4 )))) =−∫(du/( (√((1+u)^2 −2u^2 ))))=−∫(du/( (√(1+2u−u^2 )))) =−∫(du/( (√(2−(u−1)^2 ))))=Arcos(((u−1)/( (√2))))+C
$$\mathrm{a}. \\ $$$$\mathrm{I}=\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{2}}}\:,\:\mathrm{u}=\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\Rightarrow\mathrm{du}=\frac{−\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{I}=\int\frac{−\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \mathrm{u}}{\:\sqrt{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}}}\mathrm{du}=−\int\frac{\mathrm{udu}}{\:\sqrt{\left(\mathrm{u}+\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2u}^{\mathrm{4}} }} \\ $$$$\:\:=−\int\frac{\mathrm{du}}{\:\sqrt{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} −\mathrm{2u}^{\mathrm{2}} }}=−\int\frac{\mathrm{du}}{\:\sqrt{\mathrm{1}+\mathrm{2u}−\mathrm{u}^{\mathrm{2}} }} \\ $$$$\:\:=−\int\frac{\mathrm{du}}{\:\sqrt{\mathrm{2}−\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{2}} }}=\mathrm{Arcos}\left(\frac{\mathrm{u}−\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{C} \\ $$
Commented by peter frank last updated on 22/Aug/20
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by mathmax by abdo last updated on 22/Aug/20
a) I =∫(dx/((x+1)(√(x^2 +4x +2)))) ⇒ I =∫ (dx/((x+1)(√((x+2)^2 −2)))) =_(x+2 =(√2)ch(t)) ∫ (((√2)sh(t))/((−2+(√2)cht +1)(√2)sh(t)))dt =∫ (dt/(−1+(√2)((e^t +e^(−t) )/2))) =∫ ((2dt)/(−2+(√2)e^t +(√2)e^(−t) )) =_(e^t =u) 2 ∫ (du/(u(−2+(√2)u +(√2)u^(−1) ))) =2 ∫ (du/(−2u+(√2)u^2 +(√2))) =(√2)∫ (du/(u^2 −(√2)u +1)) =(√2)∫ (du/(u^2 −2(1/( (√2)))u +(1/2)+(1/2))) =(√2)∫ (du/((u−(1/( (√2))))^2 +(1/2))) =_(u−(1/( (√2)))=(z/( (√2)))) (√2)∫ (dz/( (√2).(1/2)(1+z^2 ))) =∫ ((2dz)/(1+z^2 )) =2arctanz +C =2arctan(u(√2)−1) +C we have t =argch(((x+2)/( (√2)))) =ln(((x+2)/( (√2)))+(√((((x+2)/( (√2))))^2 −1))) ⇒ u =e^t =((x+2)/( (√2))) +(√((((x+2)/( (√2))))^2 −1)) ⇒ I =2arctan((√2){((x+2)/( (√2)))+(√((((x+2)/( (√2))))^2 −1))}) +C
$$\left.\mathrm{a}\right)\:\mathrm{I}\:=\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4x}\:+\mathrm{2}}}\:\Rightarrow\:\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}}} \\ $$$$=_{\mathrm{x}+\mathrm{2}\:=\sqrt{\mathrm{2}}\mathrm{ch}\left(\mathrm{t}\right)} \:\:\:\:\int\:\:\frac{\sqrt{\mathrm{2}}\mathrm{sh}\left(\mathrm{t}\right)}{\left(−\mathrm{2}+\sqrt{\mathrm{2}}\mathrm{cht}\:+\mathrm{1}\right)\sqrt{\mathrm{2}}\mathrm{sh}\left(\mathrm{t}\right)}\mathrm{dt} \\ $$$$=\int\:\frac{\mathrm{dt}}{−\mathrm{1}+\sqrt{\mathrm{2}}\frac{\mathrm{e}^{\mathrm{t}} \:+\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}}\:=\int\:\:\:\frac{\mathrm{2dt}}{−\mathrm{2}+\sqrt{\mathrm{2}}\mathrm{e}^{\mathrm{t}} \:+\sqrt{\mathrm{2}}\mathrm{e}^{−\mathrm{t}} } \\ $$$$=_{\mathrm{e}^{\mathrm{t}} \:=\mathrm{u}} \:\:\:\:\mathrm{2}\:\int\:\:\:\frac{\mathrm{du}}{\mathrm{u}\left(−\mathrm{2}+\sqrt{\mathrm{2}}\mathrm{u}\:+\sqrt{\mathrm{2}}\mathrm{u}^{−\mathrm{1}} \right)}\:=\mathrm{2}\:\int\:\:\frac{\mathrm{du}}{−\mathrm{2u}+\sqrt{\mathrm{2}}\mathrm{u}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}} \\ $$$$=\sqrt{\mathrm{2}}\int\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}\mathrm{u}\:+\mathrm{1}}\:=\sqrt{\mathrm{2}}\int\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} −\mathrm{2}\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{u}\:+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\sqrt{\mathrm{2}}\int\:\:\frac{\mathrm{du}}{\left(\mathrm{u}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}}}\:=_{\mathrm{u}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\frac{\mathrm{z}}{\:\sqrt{\mathrm{2}}}} \:\:\sqrt{\mathrm{2}}\int\:\:\:\frac{\mathrm{dz}}{\:\sqrt{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)}\:=\int\:\frac{\mathrm{2dz}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} } \\ $$$$=\mathrm{2arctanz}\:+\mathrm{C}\:=\mathrm{2arctan}\left(\mathrm{u}\sqrt{\mathrm{2}}−\mathrm{1}\right)\:+\mathrm{C} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{t}\:=\mathrm{argch}\left(\frac{\mathrm{x}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}\right)\:=\mathrm{ln}\left(\frac{\mathrm{x}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}+\sqrt{\left(\frac{\mathrm{x}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} −\mathrm{1}}\right)\:\Rightarrow \\ $$$$\mathrm{u}\:=\mathrm{e}^{\mathrm{t}} \:=\frac{\mathrm{x}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}\:+\sqrt{\left(\frac{\mathrm{x}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} −\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{2arctan}\left(\sqrt{\mathrm{2}}\left\{\frac{\mathrm{x}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}+\sqrt{\left(\frac{\mathrm{x}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} −\mathrm{1}}\right\}\right)\:+\mathrm{C} \\ $$
Commented by mathmax by abdo last updated on 22/Aug/20
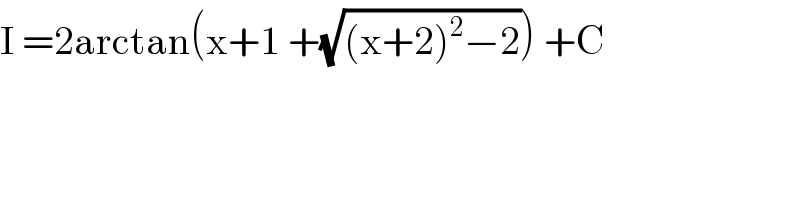
I =2arctan(x+1 +(√((x+2)^2 −2))) +C
$$\mathrm{I}\:=\mathrm{2arctan}\left(\mathrm{x}+\mathrm{1}\:+\sqrt{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}}\right)\:+\mathrm{C} \\ $$
Commented by peter frank last updated on 22/Aug/20
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mathmax by abdo last updated on 22/Aug/20
you are welcome
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Answered by mathmax by abdo last updated on 22/Aug/20
b) A =∫ (dx/((x^2 +1)(√(x^2 +2)))) ⇒ A =_(x=(√2)sht) ∫ (((√2)ch(t))/((2sh^2 t +1)(√2)ch(t)))dt =∫ (dt/(2.((ch(2t)−1)/2)+1)) =∫ (dt/(ch(2t))) =_(2t=u) ∫ (du/(2ch(u))) = ∫ (du/(e^u +e^(−u) )) =_(e^u =z) ∫ (dz/(z(z+z^(−1) ))) =∫ (dz/(z^2 +1)) =arctanz +c =arctan(z) +c = arctan(e^u ) +c =arctan(e^(2t) )+c t =argsh((x/( (√2)))) =ln((x/( (√2)))+(√(1+(x^2 /2)))) ⇒e^(2t) =((x/2)+(√(1+(x^2 /2))))^2 ⇒ A =arctan{((x/2)+(√(1+(x^2 /2))))^2 } +C
$$\left.\mathrm{b}\right)\:\mathrm{A}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}}}\:\Rightarrow\:\mathrm{A}\:=_{\mathrm{x}=\sqrt{\mathrm{2}}\mathrm{sht}} \:\:\:\int\:\:\frac{\sqrt{\mathrm{2}}\mathrm{ch}\left(\mathrm{t}\right)}{\left(\mathrm{2sh}^{\mathrm{2}} \mathrm{t}\:+\mathrm{1}\right)\sqrt{\mathrm{2}}\mathrm{ch}\left(\mathrm{t}\right)}\mathrm{dt} \\ $$$$=\int\:\:\frac{\mathrm{dt}}{\mathrm{2}.\frac{\mathrm{ch}\left(\mathrm{2t}\right)−\mathrm{1}}{\mathrm{2}}+\mathrm{1}}\:=\int\:\:\frac{\mathrm{dt}}{\mathrm{ch}\left(\mathrm{2t}\right)}\:=_{\mathrm{2t}=\mathrm{u}} \:\:\int\:\:\frac{\mathrm{du}}{\mathrm{2ch}\left(\mathrm{u}\right)} \\ $$$$=\:\int\:\:\frac{\mathrm{du}}{\mathrm{e}^{\mathrm{u}} \:+\mathrm{e}^{−\mathrm{u}} }\:\:=_{\mathrm{e}^{\mathrm{u}} \:=\mathrm{z}} \:\:\:\:\int\:\:\frac{\mathrm{dz}}{\mathrm{z}\left(\mathrm{z}+\mathrm{z}^{−\mathrm{1}} \right)}\:=\int\:\frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\:=\mathrm{arctanz}\:+\mathrm{c} \\ $$$$=\mathrm{arctan}\left(\mathrm{z}\right)\:+\mathrm{c}\:=\:\mathrm{arctan}\left(\mathrm{e}^{\mathrm{u}} \right)\:+\mathrm{c}\:=\mathrm{arctan}\left(\mathrm{e}^{\mathrm{2t}} \right)+\mathrm{c} \\ $$$$\mathrm{t}\:=\mathrm{argsh}\left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)\:=\mathrm{ln}\left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}}\right)\:\Rightarrow\mathrm{e}^{\mathrm{2t}} \:=\left(\frac{\mathrm{x}}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{A}\:=\mathrm{arctan}\left\{\left(\frac{\mathrm{x}}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}}\right)^{\mathrm{2}} \right\}\:+\mathrm{C} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *