Menu Close

Question-109284

Tinku Tara 0 Comments
Pin




Question Number 109284 by bobhans last updated on 22/Aug/20
Answered by abdomsup last updated on 22/Aug/20
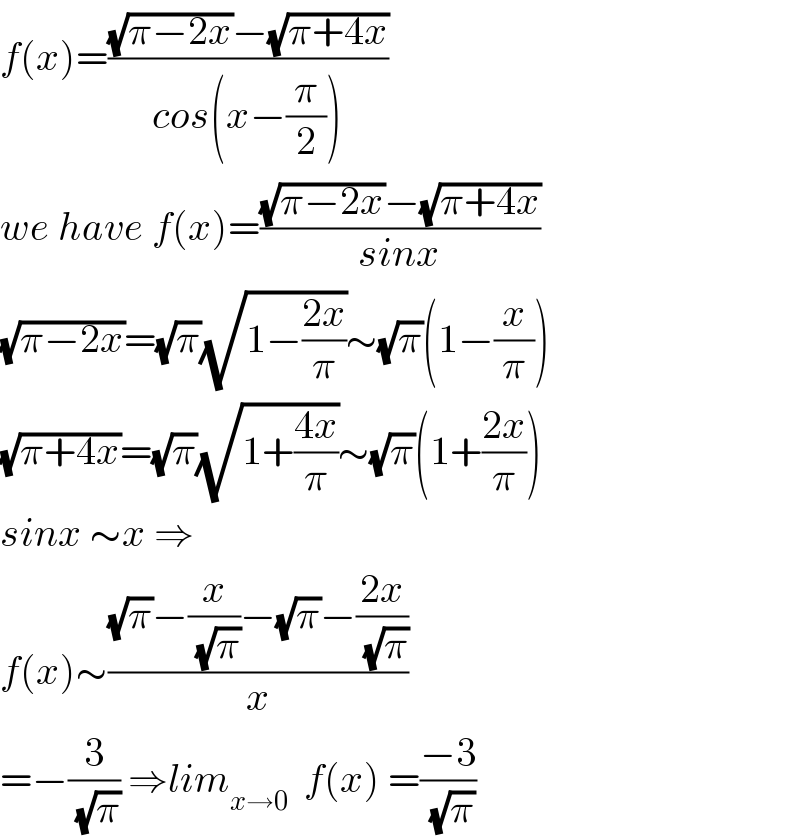
f(x)=(((√(π−2x))−(√(π+4x)))/(cos(x−(π/2)))) we have f(x)=(((√(π−2x))−(√(π+4x)))/(sinx)) (√(π−2x))=(√π)(√(1−((2x)/π)))∼(√π)(1−(x/π)) (√(π+4x))=(√π)(√(1+((4x)/π)))∼(√π)(1+((2x)/π)) sinx ∼x ⇒ f(x)∼(((√π)−(x/( (√π)))−(√π)−((2x)/( (√π))))/x) =−(3/( (√π))) ⇒lim_(x→0) f(x) =((−3)/( (√π)))
$${f}\left({x}\right)=\frac{\sqrt{\pi−\mathrm{2}{x}}−\sqrt{\pi+\mathrm{4}{x}}}{{cos}\left({x}−\frac{\pi}{\mathrm{2}}\right)} \\ $$$${we}\:{have}\:{f}\left({x}\right)=\frac{\sqrt{\pi−\mathrm{2}{x}}−\sqrt{\pi+\mathrm{4}{x}}}{{sinx}} \\ $$$$\sqrt{\pi−\mathrm{2}{x}}=\sqrt{\pi}\sqrt{\mathrm{1}−\frac{\mathrm{2}{x}}{\pi}}\sim\sqrt{\pi}\left(\mathrm{1}−\frac{{x}}{\pi}\right) \\ $$$$\sqrt{\pi+\mathrm{4}{x}}=\sqrt{\pi}\sqrt{\mathrm{1}+\frac{\mathrm{4}{x}}{\pi}}\sim\sqrt{\pi}\left(\mathrm{1}+\frac{\mathrm{2}{x}}{\pi}\right) \\ $$$${sinx}\:\sim{x}\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\frac{\sqrt{\pi}−\frac{{x}}{\:\sqrt{\pi}}−\sqrt{\pi}−\frac{\mathrm{2}{x}}{\:\sqrt{\pi}}}{{x}} \\ $$$$=−\frac{\mathrm{3}}{\:\sqrt{\pi}}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:{f}\left({x}\right)\:=\frac{−\mathrm{3}}{\:\sqrt{\pi}} \\ $$
Answered by abdomsup last updated on 22/Aug/20
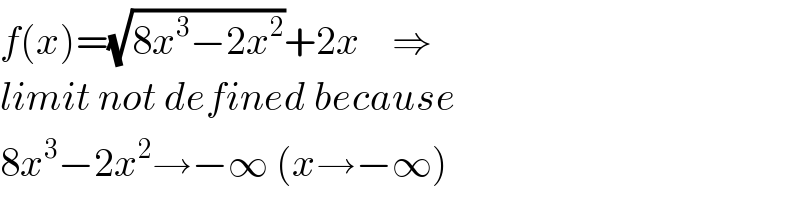
f(x)=(√(8x^3 −2x^2 ))+2x ⇒ limit not defined because 8x^3 −2x^2 →−∞ (x→−∞)
$${f}\left({x}\right)=\sqrt{\mathrm{8}{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} }+\mathrm{2}{x}\:\:\:\:\Rightarrow \\ $$$${limit}\:{not}\:{defined}\:{because} \\ $$$$\mathrm{8}{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} \rightarrow−\infty\:\left({x}\rightarrow−\infty\right) \\ $$
Answered by abdomsup last updated on 22/Aug/20
f(x)=(((x−2)/(x+2)))^(3x−1) ⇒ f(x)=e^((3x−1)ln(((x−2)/(x+2)))) =e^((3x−1)ln(1−(4/(x+2)))) if x is real limit not defined x=0 ⇒1−(4/(x+2))<0 ! if x complex ⇒f(x)=e^((3x−1)(iπ)ln((4/(x+2))−1)) ⇒lim_(x→0) f(x)=e^(−iπln(1)) =e^0 =1
$${f}\left({x}\right)=\left(\frac{{x}−\mathrm{2}}{{x}+\mathrm{2}}\right)^{\mathrm{3}{x}−\mathrm{1}} \:\:\Rightarrow \\ $$$${f}\left({x}\right)={e}^{\left(\mathrm{3}{x}−\mathrm{1}\right){ln}\left(\frac{{x}−\mathrm{2}}{{x}+\mathrm{2}}\right)} \\ $$$$={e}^{\left(\mathrm{3}{x}−\mathrm{1}\right){ln}\left(\mathrm{1}−\frac{\mathrm{4}}{{x}+\mathrm{2}}\right)} \:{if}\:{x}\:{is}\:{real} \\ $$$${limit}\:{not}\:{defined}\:\:{x}=\mathrm{0}\:\Rightarrow\mathrm{1}−\frac{\mathrm{4}}{{x}+\mathrm{2}}<\mathrm{0} \\ $$$$! \\ $$$${if}\:{x}\:{complex}\:\Rightarrow{f}\left({x}\right)={e}^{\left(\mathrm{3}{x}−\mathrm{1}\right)\left({i}\pi\right){ln}\left(\frac{\mathrm{4}}{{x}+\mathrm{2}}−\mathrm{1}\right)} \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)={e}^{−{i}\pi{ln}\left(\mathrm{1}\right)} \:={e}^{\mathrm{0}} \:=\mathrm{1} \\ $$
Commented by abdomsup last updated on 22/Aug/20
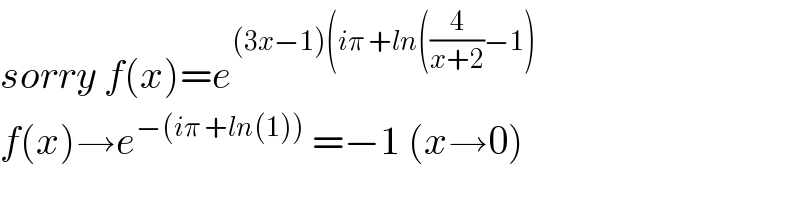
sorry f(x)=e^((3x−1)(iπ +ln((4/(x+2))−1)) f(x)→e^(−(iπ +ln(1))) =−1 (x→0)
$${sorry}\:{f}\left({x}\right)={e}^{\left(\mathrm{3}{x}−\mathrm{1}\right)\left({i}\pi\:+{ln}\left(\frac{\mathrm{4}}{{x}+\mathrm{2}}−\mathrm{1}\right)\right.} \\ $$$${f}\left({x}\right)\rightarrow{e}^{−\left({i}\pi\:+{ln}\left(\mathrm{1}\right)\right)} \:=−\mathrm{1}\:\left({x}\rightarrow\mathrm{0}\right) \\ $$
Answered by mathmax by abdo last updated on 22/Aug/20
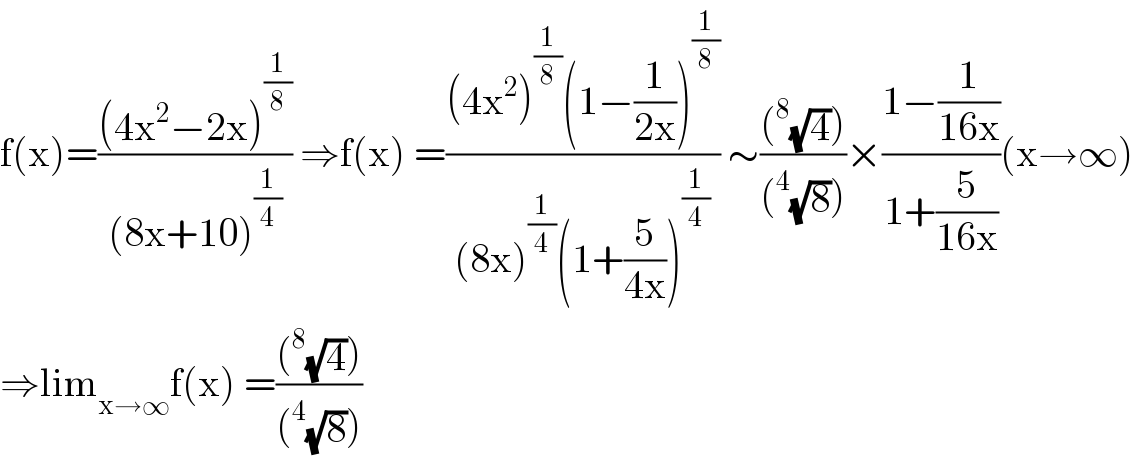
f(x)=(((4x^2 −2x)^(1/8) )/((8x+10)^(1/4) )) ⇒f(x) =(((4x^2 )^(1/8) (1−(1/(2x)))^(1/8) )/((8x)^(1/4) (1+(5/(4x)))^(1/4) )) ∼(((^8 (√4)))/((^4 (√8))))×((1−(1/(16x)))/(1+(5/(16x))))(x→∞) ⇒lim_(x→∞) f(x) =(((^8 (√4)))/((^4 (√8))))
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\left(\mathrm{4x}^{\mathrm{2}} −\mathrm{2x}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} }{\left(\mathrm{8x}+\mathrm{10}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\left(\mathrm{4x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{8}}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2x}}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} }{\left(\mathrm{8x}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \left(\mathrm{1}+\frac{\mathrm{5}}{\mathrm{4x}}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }\:\sim\frac{\left(^{\mathrm{8}} \sqrt{\mathrm{4}}\right)}{\left(^{\mathrm{4}} \sqrt{\mathrm{8}}\right)}×\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{16x}}}{\mathrm{1}+\frac{\mathrm{5}}{\mathrm{16x}}}\left(\mathrm{x}\rightarrow\infty\right) \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\frac{\left(^{\mathrm{8}} \sqrt{\mathrm{4}}\right)}{\left(^{\mathrm{4}} \sqrt{\mathrm{8}}\right)} \\ $$
Answered by mathmax by abdo last updated on 22/Aug/20
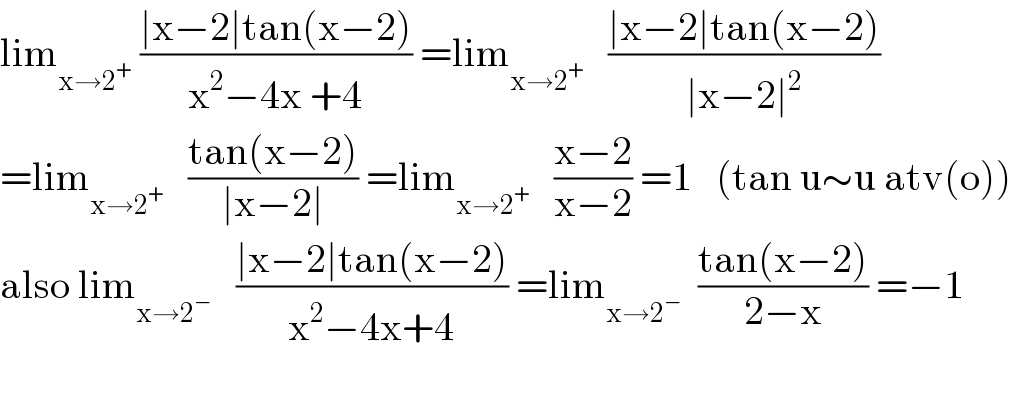
lim_(x→2^+ ) ((∣x−2∣tan(x−2))/(x^2 −4x +4)) =lim_(x→2^+ ) ((∣x−2∣tan(x−2))/(∣x−2∣^2 )) =lim_(x→2^+ ) ((tan(x−2))/(∣x−2∣)) =lim_(x→2^+ ) ((x−2)/(x−2)) =1 (tan u∼u atv(o)) also lim_(x→2^− ) ((∣x−2∣tan(x−2))/(x^2 −4x+4)) =lim_(x→2^− ) ((tan(x−2))/(2−x)) =−1
$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{2}^{+} } \:\frac{\mid\mathrm{x}−\mathrm{2}\mid\mathrm{tan}\left(\mathrm{x}−\mathrm{2}\right)}{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}\:+\mathrm{4}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{2}^{+} } \:\:\:\frac{\mid\mathrm{x}−\mathrm{2}\mid\mathrm{tan}\left(\mathrm{x}−\mathrm{2}\right)}{\mid\mathrm{x}−\mathrm{2}\mid^{\mathrm{2}} } \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{2}^{+} } \:\:\:\frac{\mathrm{tan}\left(\mathrm{x}−\mathrm{2}\right)}{\mid\mathrm{x}−\mathrm{2}\mid}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{2}^{+} } \:\:\:\frac{\mathrm{x}−\mathrm{2}}{\mathrm{x}−\mathrm{2}}\:=\mathrm{1}\:\:\:\left(\mathrm{tan}\:\mathrm{u}\sim\mathrm{u}\:\mathrm{atv}\left(\mathrm{o}\right)\right) \\ $$$$\mathrm{also}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{2}^{−} } \:\:\:\frac{\mid\mathrm{x}−\mathrm{2}\mid\mathrm{tan}\left(\mathrm{x}−\mathrm{2}\right)}{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{4}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{2}^{−} } \:\:\frac{\mathrm{tan}\left(\mathrm{x}−\mathrm{2}\right)}{\mathrm{2}−\mathrm{x}}\:=−\mathrm{1} \\ $$$$ \\ $$
Answered by john santu last updated on 22/Aug/20
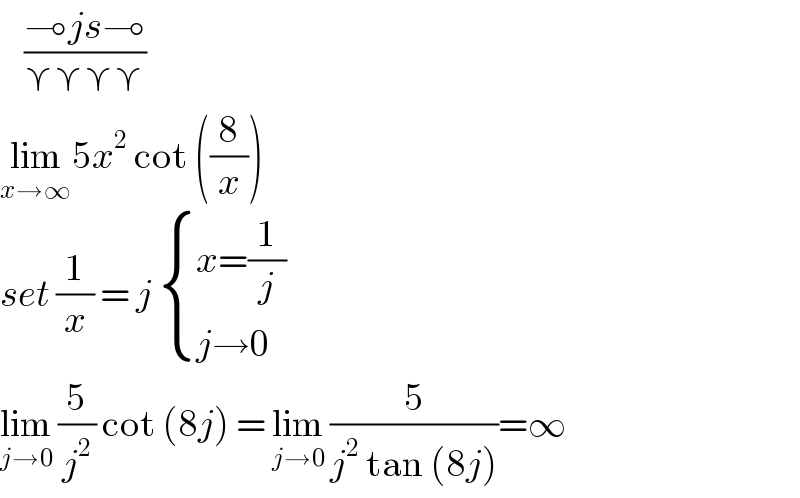
((⊸js⊸)/(⋎⋎⋎⋎)) lim_(x→∞) 5x^2 cot ((8/x)) set (1/x) = j { ((x=(1/j))),((j→0)) :} lim_(j→0) (5/j^2 ) cot (8j) = lim_(j→0) (5/(j^2 tan (8j)))=∞
$$\:\:\:\:\frac{\multimap{js}\multimap}{\curlyvee\curlyvee\curlyvee\curlyvee} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}5}{x}^{\mathrm{2}} \:\mathrm{cot}\:\left(\frac{\mathrm{8}}{{x}}\right) \\ $$$${set}\:\frac{\mathrm{1}}{{x}}\:=\:{j}\:\begin{cases}{{x}=\frac{\mathrm{1}}{{j}}}\\{{j}\rightarrow\mathrm{0}}\end{cases} \\ $$$$\underset{{j}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5}}{{j}^{\mathrm{2}} }\:\mathrm{cot}\:\left(\mathrm{8}{j}\right)\:=\:\underset{{j}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5}}{{j}^{\mathrm{2}} \:\mathrm{tan}\:\left(\mathrm{8}{j}\right)}=\infty \\ $$
Answered by john santu last updated on 22/Aug/20
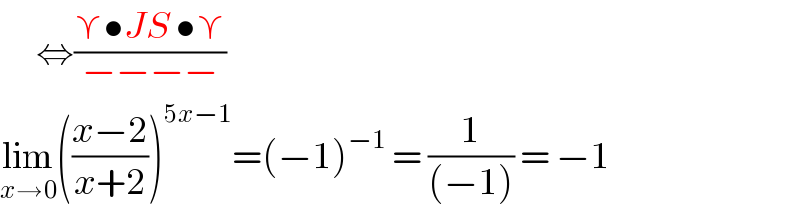
⇔((⋎•JS •⋎)/(−−−−)) lim_(x→0) (((x−2)/(x+2)))^(5x−1) =(−1)^(−1) = (1/((−1))) = −1
$$\:\:\:\:\:\:\Leftrightarrow\frac{\curlyvee\bullet{JS}\:\bullet\curlyvee}{−−−−} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{x}−\mathrm{2}}{{x}+\mathrm{2}}\right)^{\mathrm{5}{x}−\mathrm{1}} =\left(−\mathrm{1}\right)^{−\mathrm{1}} \:=\:\frac{\mathrm{1}}{\left(−\mathrm{1}\right)}\:=\:−\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 22/Aug/20
sir js what s domain of definition of x→(((x−2)/(x+2)))^(5x−1) ...?
$$\mathrm{sir}\:\mathrm{js}\:\mathrm{what}\:\mathrm{s}\:\mathrm{domain}\:\mathrm{of}\:\mathrm{definition}\:\mathrm{of}\:\mathrm{x}\rightarrow\left(\frac{\mathrm{x}−\mathrm{2}}{\mathrm{x}+\mathrm{2}}\right)^{\mathrm{5x}−\mathrm{1}} \:\:…? \\ $$
Commented by john santu last updated on 22/Aug/20
x≠−2
$${x}\neq−\mathrm{2} \\ $$
Commented by mathmax by abdo last updated on 22/Aug/20
S =Σ_(n=0) ^∞ ∫_n ^(n+1) (((−1)^([x]) )/(2+cos(n[x]))) dx =Σ_(n=0) ^∞ ∫_n ^(n+1) (((−1)^n )/(2+cos(nx)))dx =Σ_(n=0) ^∞ (−1)^n ∫_n ^(n+1) (dx/(2+cos(nx))) =Σ_(n=0) ^∞ (−1)^n u_n u_n =_(nx=t) ∫_n^2 ^(n^2 +n) (dt/(n(2+cos(t)))) =_(tan((t/2))=u) (1/n) ∫_(tan((n^2 /2))) ^(tan(((n^2 +n)/2))) ((2du)/((1+u^2 )(2+((1−u^2 )/(1+u^2 ))))) =(2/n) ∫_(tan((n^2 /2))) ^(tan(((n^2 +n)/2))) (du/(2+2u^2 +1−u^2 )) =(2/n)∫_(tan((n^2 /2))) ^(tan(((n^2 +n)/2))) (du/(u^2 +3)) =_(u=(√3)z) (2/n) ∫_((1/( (√3)))tan((n^2 /2))) ^((1/( (√3)))tan(((n^2 +n)/2))) (((√3)dz)/(3(1+z^2 ))) =(2/(n(√3))){arctan((1/( (√3)))tan(((n^2 +n)/2))) −arctan((1/( (√3)))tan((n^2 /2))} ⇒ S =(2/( (√3)))Σ_(n=0) ^∞ (−1)^n {arctan((1/( (√3)))tan(((n^2 +n)/2))−arctan((1/( (√3)))tan((n^2 /2))} rest to study convergence of this serie .....
$$\mathrm{S}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{n}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\left[\mathrm{x}\right]} }{\mathrm{2}+\mathrm{cos}\left(\mathrm{n}\left[\mathrm{x}\right]\right)}\:\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{n}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2}+\mathrm{cos}\left(\mathrm{nx}\right)}\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{n}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{2}+\mathrm{cos}\left(\mathrm{nx}\right)}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}_{\mathrm{n}} \\ $$$$\mathrm{u}_{\mathrm{n}} =_{\mathrm{nx}=\mathrm{t}} \:\:\:\int_{\mathrm{n}^{\mathrm{2}} } ^{\mathrm{n}^{\mathrm{2}} \:+\mathrm{n}} \:\frac{\mathrm{dt}}{\mathrm{n}\left(\mathrm{2}+\mathrm{cos}\left(\mathrm{t}\right)\right)}\:=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{u}} \:\:\frac{\mathrm{1}}{\mathrm{n}}\:\int_{\mathrm{tan}\left(\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{2}}\right)} ^{\mathrm{tan}\left(\frac{\mathrm{n}^{\mathrm{2}} \:+\mathrm{n}}{\mathrm{2}}\right)} \:\frac{\mathrm{2du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\mathrm{2}+\frac{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\right)} \\ $$$$=\frac{\mathrm{2}}{\mathrm{n}}\:\int_{\mathrm{tan}\left(\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{2}}\right)} ^{\mathrm{tan}\left(\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{n}}{\mathrm{2}}\right)} \:\:\frac{\mathrm{du}}{\mathrm{2}+\mathrm{2u}^{\mathrm{2}} +\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\mathrm{n}}\int_{\mathrm{tan}\left(\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{2}}\right)} ^{\mathrm{tan}\left(\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{n}}{\mathrm{2}}\right)} \:\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{3}} \\ $$$$=_{\mathrm{u}=\sqrt{\mathrm{3}}\mathrm{z}} \:\:\:\:\frac{\mathrm{2}}{\mathrm{n}}\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}\left(\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{2}}\right)} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}\left(\frac{\mathrm{n}^{\mathrm{2}} \:+\mathrm{n}}{\mathrm{2}}\right)} \:\frac{\sqrt{\mathrm{3}}\mathrm{dz}}{\mathrm{3}\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)}\:=\frac{\mathrm{2}}{\mathrm{n}\sqrt{\mathrm{3}}}\left\{\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}\left(\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{n}}{\mathrm{2}}\right)\right)\right. \\ $$$$−\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}\left(\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{2}}\right)\right\}\:\Rightarrow \\ $$$$\mathrm{S}\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \left\{\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}\left(\frac{\mathrm{n}^{\mathrm{2}} \:+\mathrm{n}}{\mathrm{2}}\right)−\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}\left(\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{2}}\right)\right\}\right.\right. \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{study}\:\mathrm{convergence}\:\mathrm{of}\:\mathrm{this}\:\mathrm{serie}\:….. \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 22/Aug/20
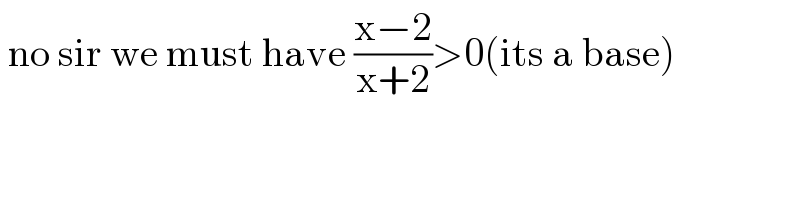
no sir we must have ((x−2)/(x+2))>0(its a base)
$$\:\mathrm{no}\:\mathrm{sir}\:\mathrm{we}\:\mathrm{must}\:\mathrm{have}\:\frac{\mathrm{x}−\mathrm{2}}{\mathrm{x}+\mathrm{2}}>\mathrm{0}\left(\mathrm{its}\:\mathrm{a}\:\mathrm{base}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *