Question Number 109307 by john santu last updated on 22/Aug/20

Answered by mr W last updated on 22/Aug/20
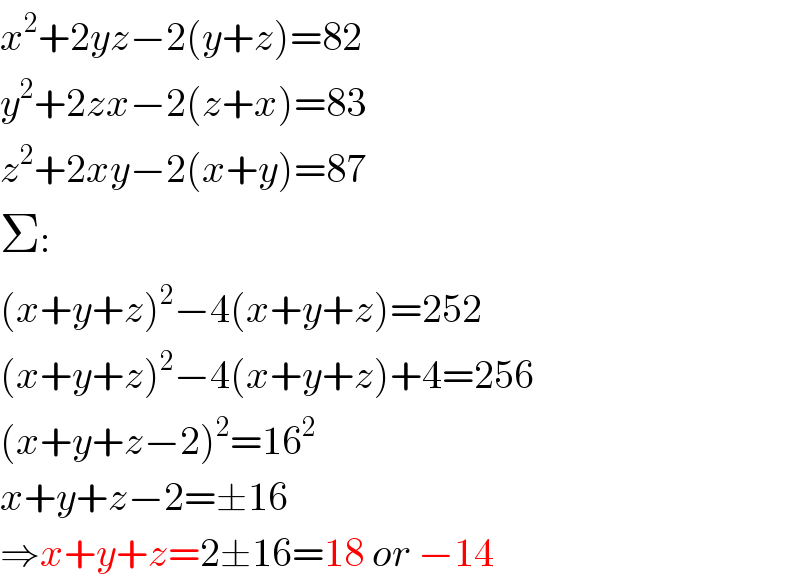
$${x}^{\mathrm{2}} +\mathrm{2}{yz}−\mathrm{2}\left({y}+{z}\right)=\mathrm{82} \\ $$$${y}^{\mathrm{2}} +\mathrm{2}{zx}−\mathrm{2}\left({z}+{x}\right)=\mathrm{83} \\ $$$${z}^{\mathrm{2}} +\mathrm{2}{xy}−\mathrm{2}\left({x}+{y}\right)=\mathrm{87} \\ $$$$\Sigma: \\ $$$$\left({x}+{y}+{z}\right)^{\mathrm{2}} −\mathrm{4}\left({x}+{y}+{z}\right)=\mathrm{252} \\ $$$$\left({x}+{y}+{z}\right)^{\mathrm{2}} −\mathrm{4}\left({x}+{y}+{z}\right)+\mathrm{4}=\mathrm{256} \\ $$$$\left({x}+{y}+{z}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{16}^{\mathrm{2}} \\ $$$${x}+{y}+{z}−\mathrm{2}=\pm\mathrm{16} \\ $$$$\Rightarrow{x}+{y}+{z}=\mathrm{2}\pm\mathrm{16}=\mathrm{18}\:{or}\:−\mathrm{14} \\ $$
Commented by bobhans last updated on 23/Aug/20
$$\:\:\:\frac{{awesome}−−−−{nice}−−−}{} \\ $$
