Question Number 109414 by qwerty111 last updated on 23/Aug/20
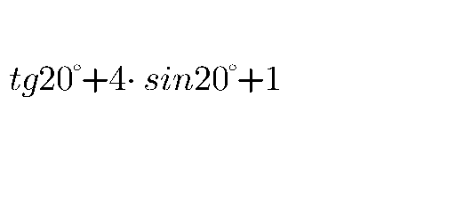
Answered by Dwaipayan Shikari last updated on 23/Aug/20

$${tan}\mathrm{20}°+\mathrm{4}{sin}\mathrm{20}° \\ $$$$\frac{\mathrm{1}}{{cos}\mathrm{20}°}\left({sin}\mathrm{20}°+\mathrm{4}{sin}\mathrm{20}°{cos}\mathrm{20}°\right) \\ $$$$\frac{\mathrm{1}}{{cos}\mathrm{20}°}\left({sin}\mathrm{20}+\mathrm{2}{sin}\mathrm{40}°\right) \\ $$$$\frac{\mathrm{1}}{{cos}\mathrm{20}°}\left(\mathrm{2}{sin}\mathrm{30}°{cos}\mathrm{10}°+{sin}\mathrm{40}°\right) \\ $$$$\frac{\mathrm{1}}{{cos}\mathrm{20}°}\left({cos}\mathrm{10}°+{cos}\mathrm{50}°\right) \\ $$$$\mathrm{2}{cos}\mathrm{30}°=\sqrt{\mathrm{3}} \\ $$$${So}\:{tan}\mathrm{20}°+\mathrm{4}{sin}\mathrm{20}°+\mathrm{1}=\sqrt{\mathrm{3}}+\mathrm{1} \\ $$
Answered by bobhans last updated on 23/Aug/20

$$\approx\:\mathrm{2}.\mathrm{732050808} \\ $$
