Question Number 109453 by mathdave last updated on 23/Aug/20

Answered by mathmax by abdo last updated on 23/Aug/20
![I =∫_0 ^(4π) ∣cosx∣ dx ⇒ I =_(x =t+2π) ∫_(−2π) ^(2π) ∣cost∣ dt =∫_(−2π) ^0 ∣cost∣ dt(→t=−u) +∫_0 ^(2π) ∣cost∣ dt =∫_0 ^(2π) ∣cosu∣du +∫_0 ^(2π) ∣cost∣ dt =2∫_0 ^(2π) ∣cost∣dt =2 ∫_0 ^π ∣cost∣ dt +2∫_π ^(2π) ∣cost∣ dt(→t=u+π) =2∫_0 ^π ∣cost∣dt +2∫_0 ^π ∣cost∣ dt =4∫_0 ^π ∣cost∣ dt =4{ ∫_0 ^(π/2) cost dt +∫_(π/2) ^π −cost dt} =4{ [sint]_0 ^(π/2) −[sint]_(π/2) ^π } =4{1−(−1)} =8 all answer given is false](https://www.tinkutara.com/question/Q109467.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{4}\pi} \mid\mathrm{cosx}\mid\:\mathrm{dx}\:\Rightarrow\:\mathrm{I}\:=_{\mathrm{x}\:=\mathrm{t}+\mathrm{2}\pi} \:\:\:\:\int_{−\mathrm{2}\pi} ^{\mathrm{2}\pi} \mid\mathrm{cost}\mid\:\mathrm{dt}\: \\ $$$$=\int_{−\mathrm{2}\pi} ^{\mathrm{0}} \:\mid\mathrm{cost}\mid\:\mathrm{dt}\left(\rightarrow\mathrm{t}=−\mathrm{u}\right)\:+\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mid\mathrm{cost}\mid\:\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mid\mathrm{cosu}\mid\mathrm{du}\:+\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\mid\mathrm{cost}\mid\:\mathrm{dt}\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mid\mathrm{cost}\mid\mathrm{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\pi} \mid\mathrm{cost}\mid\:\mathrm{dt}\:+\mathrm{2}\int_{\pi} ^{\mathrm{2}\pi} \mid\mathrm{cost}\mid\:\mathrm{dt}\left(\rightarrow\mathrm{t}=\mathrm{u}+\pi\right) \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\pi} \:\mid\mathrm{cost}\mid\mathrm{dt}\:+\mathrm{2}\int_{\mathrm{0}} ^{\pi} \:\mid\mathrm{cost}\mid\:\mathrm{dt}\:=\mathrm{4}\int_{\mathrm{0}} ^{\pi} \:\mid\mathrm{cost}\mid\:\mathrm{dt} \\ $$$$=\mathrm{4}\left\{\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cost}\:\mathrm{dt}\:+\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} −\mathrm{cost}\:\mathrm{dt}\right\} \\ $$$$=\mathrm{4}\left\{\:\left[\mathrm{sint}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\left[\mathrm{sint}\right]_{\frac{\pi}{\mathrm{2}}} ^{\pi} \right\}\:=\mathrm{4}\left\{\mathrm{1}−\left(−\mathrm{1}\right)\right\}\:=\mathrm{8}\:\:\:\mathrm{all}\:\mathrm{answer}\:\mathrm{given}\:\mathrm{is}\:\mathrm{false} \\ $$
Commented by Her_Majesty last updated on 24/Aug/20
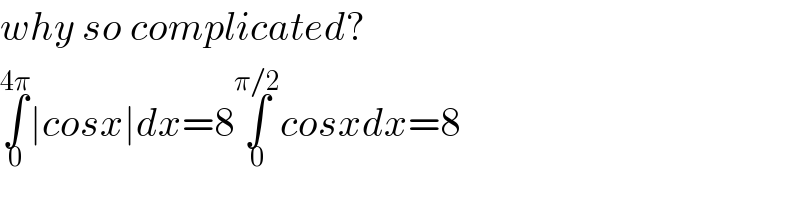
$${why}\:{so}\:{complicated}? \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{4}\pi} {\int}}\mid{cosx}\mid{dx}=\mathrm{8}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}{cosxdx}=\mathrm{8} \\ $$
Commented by malwan last updated on 24/Aug/20
$${fantastic}\:{your}\:{mjs} \\ $$
