Question Number 109460 by 150505R last updated on 23/Aug/20
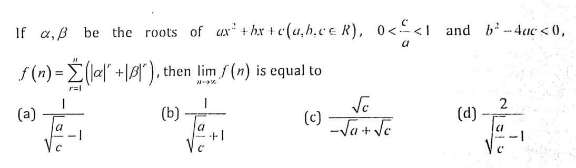
Answered by mathmax by abdo last updated on 23/Aug/20
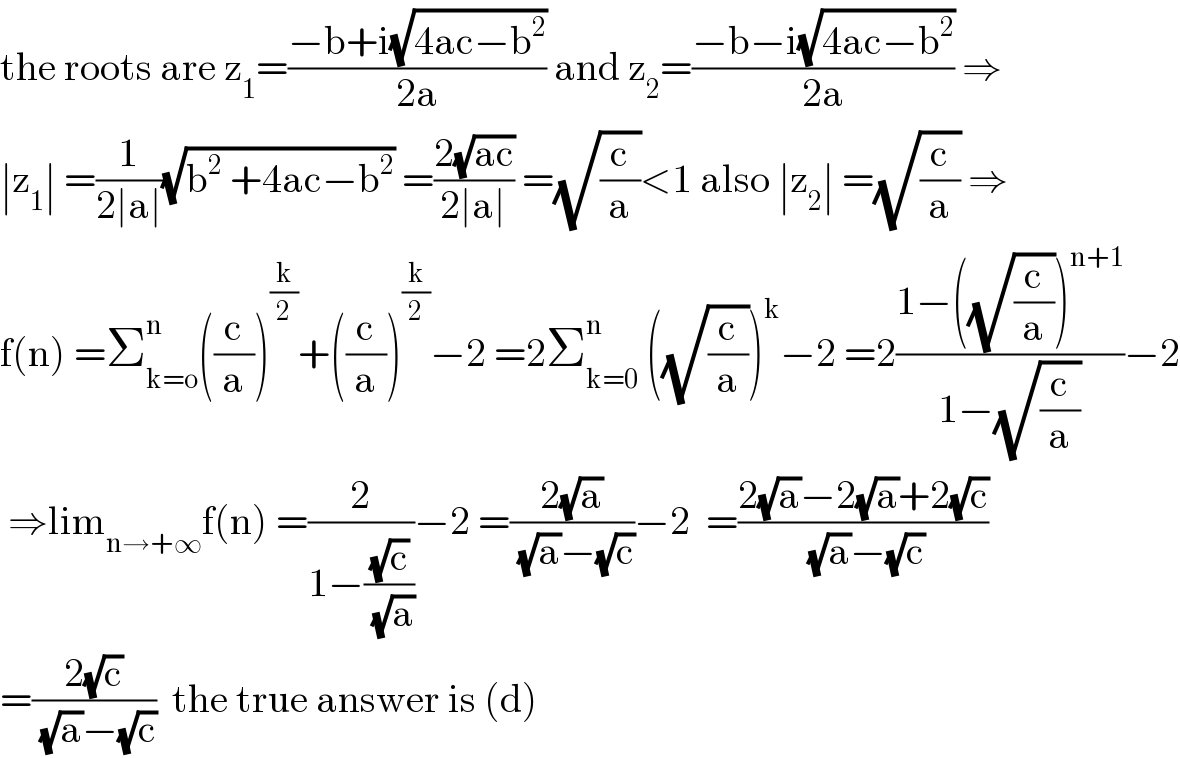
$$\mathrm{the}\:\mathrm{roots}\:\mathrm{are}\:\mathrm{z}_{\mathrm{1}} =\frac{−\mathrm{b}+\mathrm{i}\sqrt{\mathrm{4ac}−\mathrm{b}^{\mathrm{2}} }}{\mathrm{2a}}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{−\mathrm{b}−\mathrm{i}\sqrt{\mathrm{4ac}−\mathrm{b}^{\mathrm{2}} }}{\mathrm{2a}}\:\Rightarrow \\ $$$$\mid\mathrm{z}_{\mathrm{1}} \mid\:=\frac{\mathrm{1}}{\mathrm{2}\mid\mathrm{a}\mid}\sqrt{\mathrm{b}^{\mathrm{2}} \:+\mathrm{4ac}−\mathrm{b}^{\mathrm{2}} }\:=\frac{\mathrm{2}\sqrt{\mathrm{ac}}}{\mathrm{2}\mid\mathrm{a}\mid}\:=\sqrt{\frac{\mathrm{c}}{\mathrm{a}}}<\mathrm{1}\:\mathrm{also}\:\mid\mathrm{z}_{\mathrm{2}} \mid\:=\sqrt{\frac{\mathrm{c}}{\mathrm{a}}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{n}\right)\:=\sum_{\mathrm{k}=\mathrm{o}} ^{\mathrm{n}} \left(\frac{\mathrm{c}}{\mathrm{a}}\right)^{\frac{\mathrm{k}}{\mathrm{2}}} +\left(\frac{\mathrm{c}}{\mathrm{a}}\right)^{\frac{\mathrm{k}}{\mathrm{2}}} −\mathrm{2}\:=\mathrm{2}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\left(\sqrt{\frac{\mathrm{c}}{\mathrm{a}}}\right)^{\mathrm{k}} −\mathrm{2}\:=\mathrm{2}\frac{\mathrm{1}−\left(\sqrt{\frac{\mathrm{c}}{\mathrm{a}}}\right)^{\mathrm{n}+\mathrm{1}} }{\mathrm{1}−\sqrt{\frac{\mathrm{c}}{\mathrm{a}}}}−\mathrm{2} \\ $$$$\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{f}\left(\mathrm{n}\right)\:=\frac{\mathrm{2}}{\mathrm{1}−\frac{\sqrt{\mathrm{c}}}{\:\sqrt{\mathrm{a}}}}−\mathrm{2}\:=\frac{\mathrm{2}\sqrt{\mathrm{a}}}{\:\sqrt{\mathrm{a}}−\sqrt{\mathrm{c}}}−\mathrm{2}\:\:=\frac{\mathrm{2}\sqrt{\mathrm{a}}−\mathrm{2}\sqrt{\mathrm{a}}+\mathrm{2}\sqrt{\mathrm{c}}}{\:\sqrt{\mathrm{a}}−\sqrt{\mathrm{c}}} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{c}}}{\:\sqrt{\mathrm{a}}−\sqrt{\mathrm{c}}}\:\:\mathrm{the}\:\mathrm{true}\:\mathrm{answer}\:\mathrm{is}\:\left(\mathrm{d}\right) \\ $$
