Question Number 109461 by 150505R last updated on 23/Aug/20
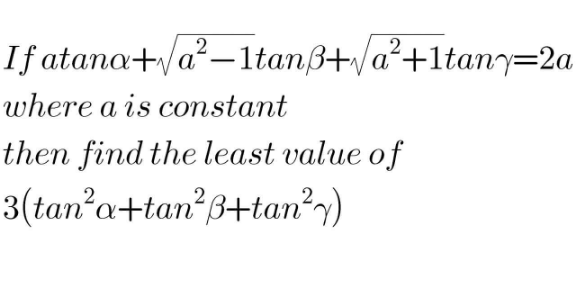
Answered by 1549442205PVT last updated on 24/Aug/20
 =(3a^2 )(tan^2 α+tan^2 β+tan^2 γ) ⇒tan^2 α+tan^2 β+tan^2 γ≥((4a^2 )/(3a^2 ))=(4/3) The equlity ocurrs if and only if { (((a/(tanα))=((√(a^2 −1))/(tanβ))=((√(a^2 +1))/(tanγ)) (1))),((tan^2 α+tan^2 β+tan^2 γ=(4/3)(2))) :} ⇒(a^2 /(tan^2 α))=((a^2 −1)/(tan^2 β))=((a^2 +1)/(tan^2 γ))=((3a^2 )/(4/3)) ⇔ { ((tan^2 α=(4/9))),((tan^2 β=((4(a^2 −1))/(9a^2 )))),((tan^2 γ=((4(a^2 +1))/(9a^2 )))) :} ⇔ { ((tanα=±(2/3))),((tanβ=±(2/(3a))(√(a^2 −1)))),((tanγ=±(2/3)(√(a^2 +1)))) :} Thus,P=3(tan^2 α+tan^2 β+tan^2 γ) has the least value equal to 4 when (𝛂,𝛃,𝛄)∈{tan^(−1) (±(2/3))+k𝛑,tan^(−1) (±(2/(3a))(√(a^2 −1)))+k𝛑,tan^(−1) (±(2/(3a))(√(a^2 +1)))+k𝛑}](https://www.tinkutara.com/question/Q109474.png)
$$\mathrm{Applying}\:\mathrm{the}\:\mathrm{inequality}\:\mathrm{AM}−\mathrm{GM}\:\mathrm{we} \\ $$$$\mathrm{have}:\left(\mathrm{2a}\right)^{\mathrm{2}} =\left(\mathrm{a}.\mathrm{tan}\alpha+\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}.\mathrm{tan}\beta+\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{1}}.\mathrm{tan}\gamma\right)^{\mathrm{2}} \\ $$$$\leqslant\left[\left(\mathrm{a}^{\mathrm{2}} +\left(\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} \right]\left(\mathrm{tan}^{\mathrm{2}} \alpha+\mathrm{tan}^{\mathrm{2}} \beta+\mathrm{tan}^{\mathrm{2}} \gamma\right)\right. \\ $$$$=\left(\mathrm{3a}^{\mathrm{2}} \right)\left(\mathrm{tan}^{\mathrm{2}} \alpha+\mathrm{tan}^{\mathrm{2}} \beta+\mathrm{tan}^{\mathrm{2}} \gamma\right) \\ $$$$\Rightarrow\mathrm{tan}^{\mathrm{2}} \alpha+\mathrm{tan}^{\mathrm{2}} \beta+\mathrm{tan}^{\mathrm{2}} \gamma\geqslant\frac{\mathrm{4a}^{\mathrm{2}} }{\mathrm{3a}^{\mathrm{2}} }=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{The}\:\mathrm{equlity}\:\mathrm{ocurrs}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if} \\ $$$$\begin{cases}{\frac{\mathrm{a}}{\mathrm{tan}\alpha}=\frac{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{tan}\beta}=\frac{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{tan}\gamma}\:\left(\mathrm{1}\right)}\\{\mathrm{tan}^{\mathrm{2}} \alpha+\mathrm{tan}^{\mathrm{2}} \beta+\mathrm{tan}^{\mathrm{2}} \gamma=\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{2}\right)}\end{cases} \\ $$$$\Rightarrow\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{tan}^{\mathrm{2}} \alpha}=\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \beta}=\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \gamma}=\frac{\mathrm{3a}^{\mathrm{2}} }{\mathrm{4}/\mathrm{3}} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{tan}^{\mathrm{2}} \alpha=\frac{\mathrm{4}}{\mathrm{9}}}\\{\mathrm{tan}^{\mathrm{2}} \beta=\frac{\mathrm{4}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{9a}^{\mathrm{2}} }}\\{\mathrm{tan}^{\mathrm{2}} \gamma=\frac{\mathrm{4}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{9a}^{\mathrm{2}} }}\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{tan}\alpha=\pm\frac{\mathrm{2}}{\mathrm{3}}}\\{\mathrm{tan}\beta=\pm\frac{\mathrm{2}}{\mathrm{3a}}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}}\\{\mathrm{tan}\gamma=\pm\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{1}}}\end{cases} \\ $$$$\mathrm{Thus},\mathrm{P}=\mathrm{3}\left(\mathrm{tan}^{\mathrm{2}} \alpha+\mathrm{tan}^{\mathrm{2}} \beta+\mathrm{tan}^{\mathrm{2}} \gamma\right) \\ $$$$\mathrm{has}\:\mathrm{the}\:\mathrm{least}\:\mathrm{value}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{4}\:\mathrm{when} \\ $$$$\left(\boldsymbol{\alpha},\boldsymbol{\beta},\boldsymbol{\gamma}\right)\in\left\{\boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \left(\pm\frac{\mathrm{2}}{\mathrm{3}}\right)+\boldsymbol{\mathrm{k}\pi},\boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \left(\pm\frac{\mathrm{2}}{\mathrm{3}\boldsymbol{\mathrm{a}}}\sqrt{\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\mathrm{1}}\right)+\boldsymbol{\mathrm{k}\pi},\boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \left(\pm\frac{\mathrm{2}}{\mathrm{3}\boldsymbol{\mathrm{a}}}\sqrt{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\mathrm{1}}\right)+\boldsymbol{\mathrm{k}\pi}\right\} \\ $$
