Question Number 109462 by 150505R last updated on 23/Aug/20
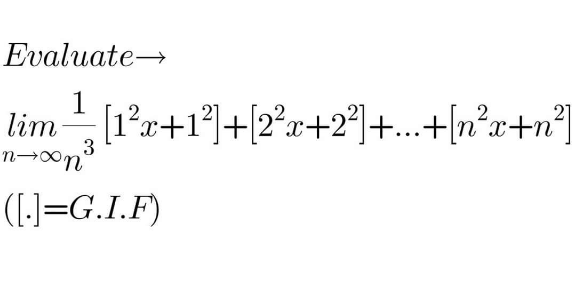
Answered by mathmax by abdo last updated on 24/Aug/20
![A_n =(1/n^3 )Σ_(k=1) ^n [k^2 x +k^2 ] ⇒ A_n =(1/n^3 )Σ_(k=1) ^n [k^2 x] +(1/n^3 )Σ_(k=1) ^n k^2 we have (1/n^3 )Σ_(k=1) ^n k^2 =(1/(6n^3 ))n(n+1)(2n+1) →(1/3)(n→+∞) we have [k^2 x] ≤k^2 x <[k^2 x] +1 ⇒k^2 x−1<[k^2 x]≤k^2 x ⇒ Σ_(k=1) ^n (k^2 x−1) <Σ_(k=1) ^n [k^2 x]≤Σ_(k=1) ^n k^2 x ⇒ ((n(n+1)(2n+1))/6)x−n <Σ_(k=1) ^n [k^2 x]≤((n(n+1)(2n+1))/6)x ⇒ ((n(n+1)(2n+1))/(6n^3 ))x−(1/n^2 )<(1/n^3 )Σ_(k=1) ^n [k^2 x]≤((n(n+1)(2n+1))/(6n^3 ))x ⇒lim_(n→+∞) (1/n^3 )Σ_(k=1) ^n [k^2 x] =(x/3) ⇒lim_(n→+∞) A_n =((x+1)/3)](https://www.tinkutara.com/question/Q109629.png)
$$\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left[\mathrm{k}^{\mathrm{2}} \mathrm{x}\:+\mathrm{k}^{\mathrm{2}} \right]\:\Rightarrow\:\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left[\mathrm{k}^{\mathrm{2}} \mathrm{x}\right]\:+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}^{\mathrm{2}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}^{\mathrm{2}} \:=\frac{\mathrm{1}}{\mathrm{6n}^{\mathrm{3}} }\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)\:\rightarrow\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{n}\rightarrow+\infty\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\:\:\:\left[\mathrm{k}^{\mathrm{2}} \mathrm{x}\right]\:\leqslant\mathrm{k}^{\mathrm{2}} \mathrm{x}\:<\left[\mathrm{k}^{\mathrm{2}} \mathrm{x}\right]\:+\mathrm{1}\:\Rightarrow\mathrm{k}^{\mathrm{2}} \mathrm{x}−\mathrm{1}<\left[\mathrm{k}^{\mathrm{2}} \mathrm{x}\right]\leqslant\mathrm{k}^{\mathrm{2}} \mathrm{x}\:\Rightarrow \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left(\mathrm{k}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)\:<\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left[\mathrm{k}^{\mathrm{2}} \mathrm{x}\right]\leqslant\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}^{\mathrm{2}} \mathrm{x}\:\Rightarrow \\ $$$$\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{6}}\mathrm{x}−\mathrm{n}\:<\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left[\mathrm{k}^{\mathrm{2}} \mathrm{x}\right]\leqslant\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{6}}\mathrm{x}\:\Rightarrow \\ $$$$\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{6n}^{\mathrm{3}} }\mathrm{x}−\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }<\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left[\mathrm{k}^{\mathrm{2}} \mathrm{x}\right]\leqslant\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{6n}^{\mathrm{3}} }\mathrm{x} \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left[\mathrm{k}^{\mathrm{2}} \mathrm{x}\right]\:=\frac{\mathrm{x}}{\mathrm{3}}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{A}_{\mathrm{n}} =\frac{\mathrm{x}+\mathrm{1}}{\mathrm{3}} \\ $$
