Question-109472

Question Number 109472 by john santu last updated on 24/Aug/20

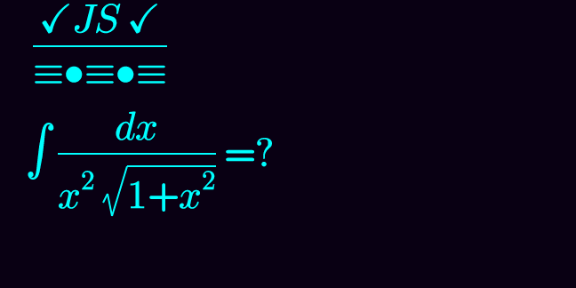
Answered by 1549442205PVT last updated on 24/Aug/20

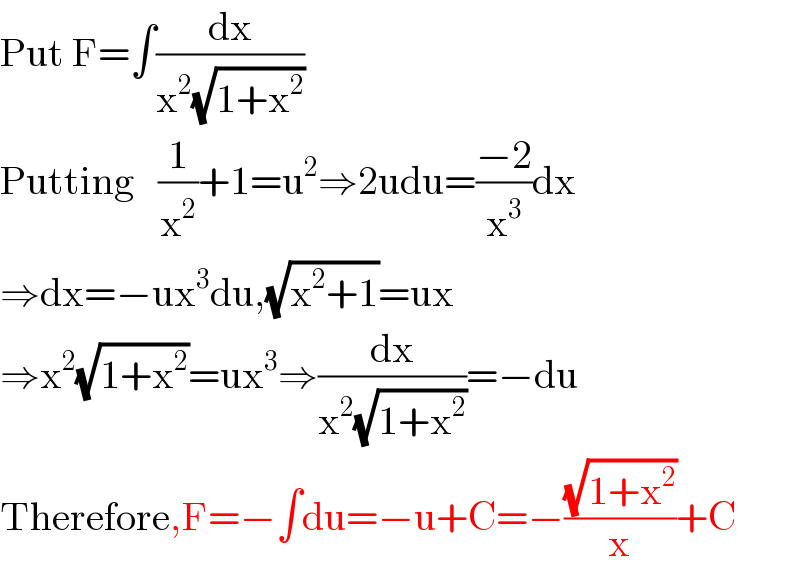
Put F=∫(dx/(x^2 (√(1+x^2 )))) Putting (1/x^2 )+1=u^2 ⇒2udu=((−2)/x^3 )dx ⇒dx=−ux^3 du,(√(x^2 +1))=ux ⇒x^2 (√(1+x^2 ))=ux^3 ⇒(dx/(x^2 (√(1+x^2 ))))=−du Therefore,F=−∫du=−u+C=−((√(1+x^2 ))/x)+C

$$\mathrm{Put}\:\mathrm{F}=\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{Putting}\:\:\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\mathrm{1}=\mathrm{u}^{\mathrm{2}} \Rightarrow\mathrm{2udu}=\frac{−\mathrm{2}}{\mathrm{x}^{\mathrm{3}} }\mathrm{dx} \\ $$$$\Rightarrow\mathrm{dx}=−\mathrm{ux}^{\mathrm{3}} \mathrm{du},\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}=\mathrm{ux} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }=\mathrm{ux}^{\mathrm{3}} \Rightarrow\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}=−\mathrm{du} \\ $$$$\mathrm{Therefore},\mathrm{F}=−\int\mathrm{du}=−\mathrm{u}+\mathrm{C}=−\frac{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}}+\mathrm{C} \\ $$

Answered by $@y@m last updated on 24/Aug/20

Let x=tan θ dx=sec^2 θdθ ∫((sec^2 θdθ)/(tan^2 θsec θ)) ∫((sec θdθ)/(tan^2 θ)) ∫((cos θ)/(sin^2 θ))dθ −(1/(sin θ))+C −cosec θ +C −(√(1+cot^2 θ))+C −(√(1+(1/x^2 ) ))+C −((√(1+x^2 ))/x) +C

$${Let}\:{x}=\mathrm{tan}\:\theta \\ $$$${dx}=\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta \\ $$$$\int\frac{\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta}{\mathrm{tan}\:^{\mathrm{2}} \theta\mathrm{sec}\:\theta} \\ $$$$\int\frac{\mathrm{sec}\:\theta{d}\theta}{\mathrm{tan}\:^{\mathrm{2}} \theta} \\ $$$$\int\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:^{\mathrm{2}} \theta}{d}\theta \\ $$$$−\frac{\mathrm{1}}{\mathrm{sin}\:\theta}+{C} \\ $$$$−\mathrm{cosec}\:\theta\:+{C} \\ $$$$−\sqrt{\mathrm{1}+\mathrm{cot}\:^{\mathrm{2}} \theta}+{C} \\ $$$$−\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:}+{C} \\ $$$$−\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}\:+{C} \\ $$

Answered by bobhans last updated on 24/Aug/20

let x = (1/v) ⇒dx = −(dv/v^2 ) I= ∫ (v^2 /( (√(1+(1/v^2 ))))) × (−(dv/v^2 )) I=−∫ (v/( (√(1+v^2 )))) dv =−(1/2)∫ ((d(1+v^2 ))/( (√(1+v^2 )))) I= −(1/2).2(√(1+v^2 ))+c = −(√(1+(1/x^2 ))) + c ((Bobhans)/(≤•≥))

$${let}\:{x}\:=\:\frac{\mathrm{1}}{{v}}\:\Rightarrow{dx}\:=\:−\frac{{dv}}{{v}^{\mathrm{2}} } \\ $$$${I}=\:\int\:\frac{{v}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{v}^{\mathrm{2}} }}}\:×\:\left(−\frac{{dv}}{{v}^{\mathrm{2}} }\right) \\ $$$${I}=−\int\:\frac{{v}}{\:\sqrt{\mathrm{1}+{v}^{\mathrm{2}} }}\:{dv}\:=−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{d}\left(\mathrm{1}+{v}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}+{v}^{\mathrm{2}} }} \\ $$$${I}=\:−\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}\sqrt{\mathrm{1}+{v}^{\mathrm{2}} }+{c}\:=\:−\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:+\:{c} \\ $$$$\:\:\:\:\:\:\frac{\mathcal{B}{obhans}}{\leqslant\bullet\geqslant} \\ $$

Answered by mathmax by abdo last updated on 24/Aug/20

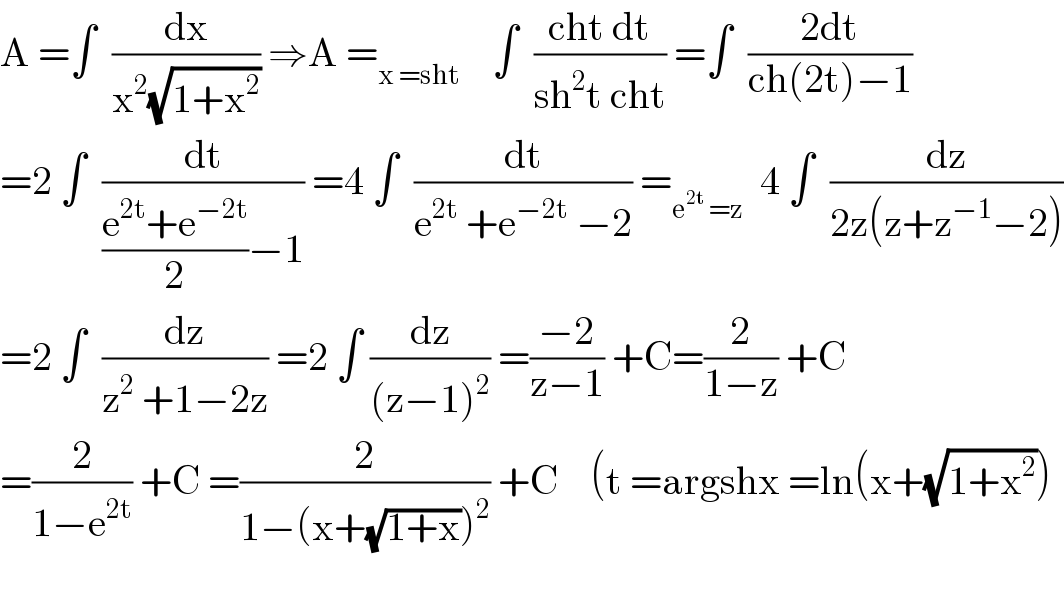
A =∫ (dx/(x^2 (√(1+x^2 )))) ⇒A =_(x =sht) ∫ ((cht dt)/(sh^2 t cht)) =∫ ((2dt)/(ch(2t)−1)) =2 ∫ (dt/(((e^(2t) +e^(−2t) )/2)−1)) =4 ∫ (dt/(e^(2t) +e^(−2t) −2)) =_(e^(2t) =z) 4 ∫ (dz/(2z(z+z^(−1) −2))) =2 ∫ (dz/(z^2 +1−2z)) =2 ∫ (dz/((z−1)^2 )) =((−2)/(z−1)) +C=(2/(1−z)) +C =(2/(1−e^(2t) )) +C =(2/(1−(x+(√(1+x)))^2 )) +C (t =argshx =ln(x+(√(1+x^2 )))

$$\mathrm{A}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\:\Rightarrow\mathrm{A}\:=_{\mathrm{x}\:=\mathrm{sht}} \:\:\:\:\int\:\:\frac{\mathrm{cht}\:\mathrm{dt}}{\mathrm{sh}^{\mathrm{2}} \mathrm{t}\:\mathrm{cht}}\:=\int\:\:\frac{\mathrm{2dt}}{\mathrm{ch}\left(\mathrm{2t}\right)−\mathrm{1}} \\ $$$$=\mathrm{2}\:\int\:\:\frac{\mathrm{dt}}{\frac{\mathrm{e}^{\mathrm{2t}} +\mathrm{e}^{−\mathrm{2t}} }{\mathrm{2}}−\mathrm{1}}\:=\mathrm{4}\:\int\:\:\frac{\mathrm{dt}}{\mathrm{e}^{\mathrm{2t}} \:+\mathrm{e}^{−\mathrm{2t}} \:−\mathrm{2}}\:=_{\mathrm{e}^{\mathrm{2t}} \:=\mathrm{z}} \:\:\mathrm{4}\:\int\:\:\frac{\mathrm{dz}}{\mathrm{2z}\left(\mathrm{z}+\mathrm{z}^{−\mathrm{1}} −\mathrm{2}\right)} \\ $$$$=\mathrm{2}\:\int\:\:\frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{2z}}\:=\mathrm{2}\:\int\:\frac{\mathrm{dz}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{−\mathrm{2}}{\mathrm{z}−\mathrm{1}}\:+\mathrm{C}=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{z}}\:+\mathrm{C} \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{e}^{\mathrm{2t}} }\:+\mathrm{C}\:=\frac{\mathrm{2}}{\mathrm{1}−\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}}\right)^{\mathrm{2}} }\:+\mathrm{C}\:\:\:\:\left(\mathrm{t}\:=\mathrm{argshx}\:=\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\right. \\ $$$$\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply