Menu Close

Question-109483

Tinku Tara 0 Comments
Pin




Question Number 109483 by ajfour last updated on 24/Aug/20
Commented by ajfour last updated on 24/Aug/20
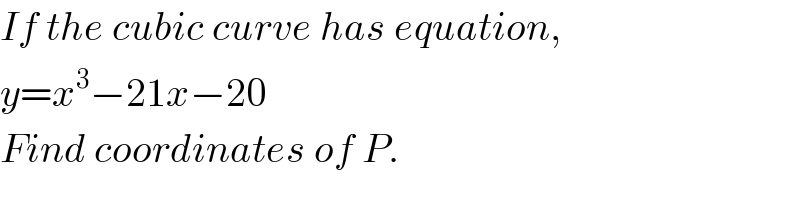
If the cubic curve has equation, y=x^3 −21x−20 Find coordinates of P.
$${If}\:{the}\:{cubic}\:{curve}\:{has}\:{equation}, \\ $$$${y}={x}^{\mathrm{3}} −\mathrm{21}{x}−\mathrm{20} \\ $$$${Find}\:{coordinates}\:{of}\:{P}. \\ $$
Commented by ajfour last updated on 24/Aug/20
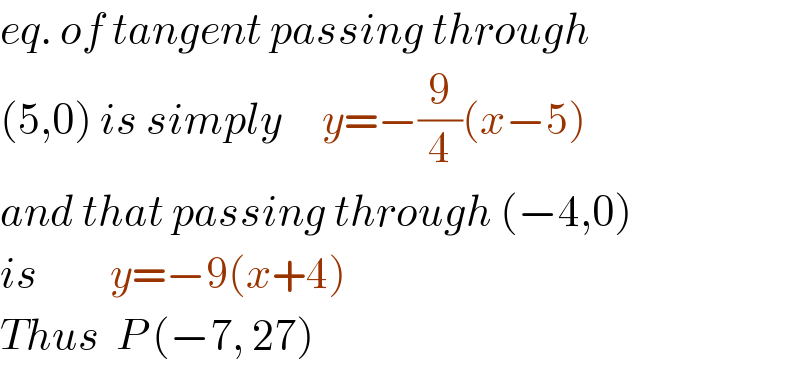
eq. of tangent passing through (5,0) is simply y=−(9/4)(x−5) and that passing through (−4,0) is y=−9(x+4) Thus P (−7, 27)
$${eq}.\:{of}\:{tangent}\:{passing}\:{through} \\ $$$$\left(\mathrm{5},\mathrm{0}\right)\:{is}\:{simply}\:\:\:\:\:{y}=−\frac{\mathrm{9}}{\mathrm{4}}\left({x}−\mathrm{5}\right) \\ $$$${and}\:{that}\:{passing}\:{through}\:\left(−\mathrm{4},\mathrm{0}\right) \\ $$$${is}\:\:\:\:\:\:\:\:\:{y}=−\mathrm{9}\left({x}+\mathrm{4}\right) \\ $$$${Thus}\:\:{P}\:\left(−\mathrm{7},\:\mathrm{27}\right) \\ $$
Answered by 1549442205PVT last updated on 25/Aug/20
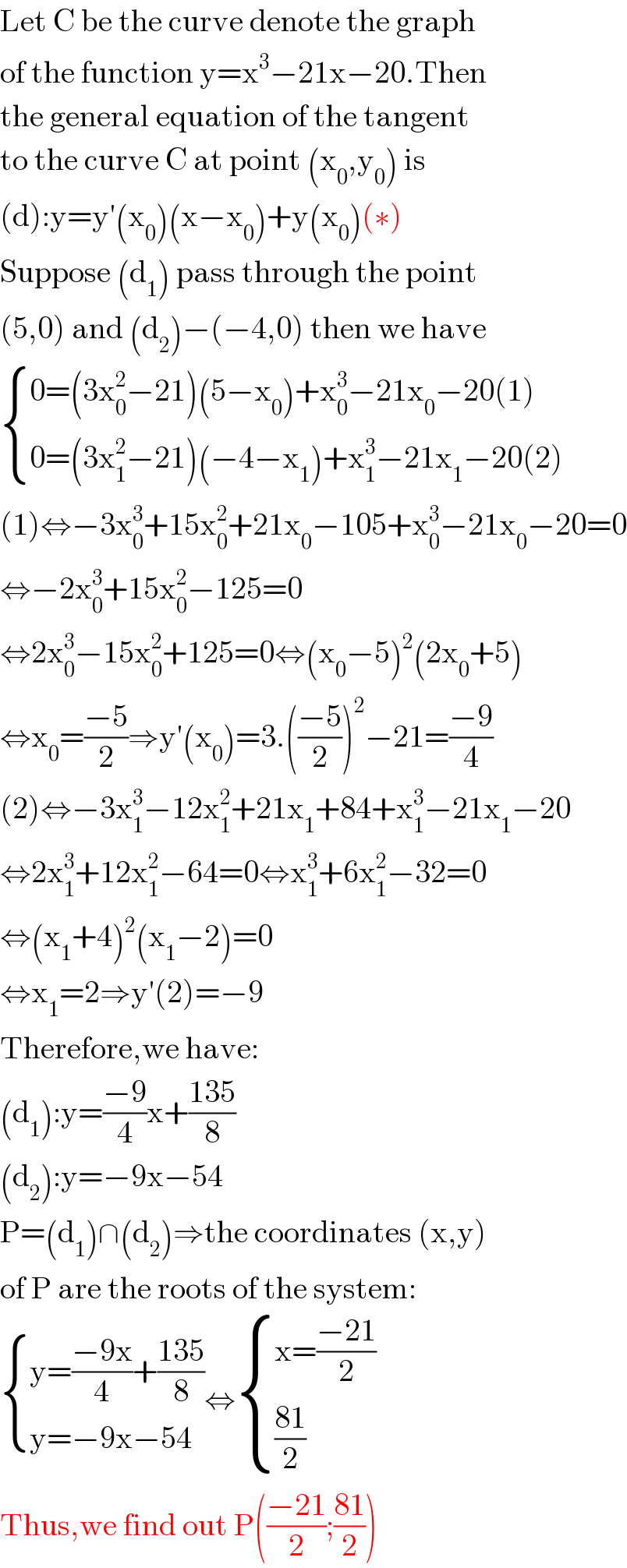
Let C be the curve denote the graph of the function y=x^3 −21x−20.Then the general equation of the tangent to the curve C at point (x_0 ,y_0 ) is (d):y=y′(x_0 )(x−x_0 )+y(x_0 )(∗) Suppose (d_1 ) pass through the point (5,0) and (d_2 )−(−4,0) then we have { ((0=(3x_0 ^2 −21)(5−x_0 )+x_0 ^3 −21x_0 −20(1))),((0=(3x_1 ^2 −21)(−4−x_1 )+x_1 ^3 −21x_1 −20(2))) :} (1)⇔−3x_0 ^3 +15x_0 ^2 +21x_0 −105+x_0 ^3 −21x_0 −20=0 ⇔−2x_0 ^3 +15x_0 ^2 −125=0 ⇔2x_0 ^3 −15x_0 ^2 +125=0⇔(x_0 −5)^2 (2x_0 +5) ⇔x_0 =((−5)/2)⇒y′(x_0 )=3.(((−5)/2))^2 −21=((−9)/4) (2)⇔−3x_1 ^3 −12x_1 ^2 +21x_1 +84+x_1 ^3 −21x_1 −20 ⇔2x_1 ^3 +12x_1 ^2 −64=0⇔x_1 ^3 +6x_1 ^2 −32=0 ⇔(x_1 +4)^2 (x_1 −2)=0 ⇔x_1 =2⇒y′(2)=−9 Therefore,we have: (d_1 ):y=((−9)/4)x+((135)/8) (d_2 ):y=−9x−54 P=(d_1 )∩(d_2 )⇒the coordinates (x,y) of P are the roots of the system: { ((y=((−9x)/4)+((135)/8))),((y=−9x−54)) :}⇔ { ((x=((−21)/2))),(((81)/2)) :} Thus,we find out P(((−21)/2);((81)/2))
$$\mathrm{Let}\:\mathrm{C}\:\mathrm{be}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{denote}\:\mathrm{the}\:\mathrm{graph} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:\mathrm{y}=\mathrm{x}^{\mathrm{3}} −\mathrm{21x}−\mathrm{20}.\mathrm{Then} \\ $$$$\mathrm{the}\:\mathrm{general}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{tangent} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{C}\:\mathrm{at}\:\mathrm{point}\:\left(\mathrm{x}_{\mathrm{0}} ,\mathrm{y}_{\mathrm{0}} \right)\:\mathrm{is} \\ $$$$\left(\mathrm{d}\right):\mathrm{y}=\mathrm{y}'\left(\mathrm{x}_{\mathrm{0}} \right)\left(\mathrm{x}−\mathrm{x}_{\mathrm{0}} \right)+\mathrm{y}\left(\mathrm{x}_{\mathrm{0}} \right)\left(\ast\right) \\ $$$$\mathrm{Suppose}\:\left(\mathrm{d}_{\mathrm{1}} \right)\:\mathrm{pass}\:\mathrm{through}\:\mathrm{the}\:\mathrm{point} \\ $$$$\left(\mathrm{5},\mathrm{0}\right)\:\mathrm{and}\:\left(\mathrm{d}_{\mathrm{2}} \right)−\left(−\mathrm{4},\mathrm{0}\right)\:\mathrm{then}\:\mathrm{we}\:\mathrm{have} \\ $$$$\begin{cases}{\mathrm{0}=\left(\mathrm{3x}_{\mathrm{0}} ^{\mathrm{2}} −\mathrm{21}\right)\left(\mathrm{5}−\mathrm{x}_{\mathrm{0}} \right)+\mathrm{x}_{\mathrm{0}} ^{\mathrm{3}} −\mathrm{21x}_{\mathrm{0}} −\mathrm{20}\left(\mathrm{1}\right)}\\{\mathrm{0}=\left(\mathrm{3x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{21}\right)\left(−\mathrm{4}−\mathrm{x}_{\mathrm{1}} \right)+\mathrm{x}_{\mathrm{1}} ^{\mathrm{3}} −\mathrm{21x}_{\mathrm{1}} −\mathrm{20}\left(\mathrm{2}\right)}\end{cases} \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow−\mathrm{3x}_{\mathrm{0}} ^{\mathrm{3}} +\mathrm{15x}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{21x}_{\mathrm{0}} −\mathrm{105}+\mathrm{x}_{\mathrm{0}} ^{\mathrm{3}} −\mathrm{21x}_{\mathrm{0}} −\mathrm{20}=\mathrm{0} \\ $$$$\Leftrightarrow−\mathrm{2x}_{\mathrm{0}} ^{\mathrm{3}} +\mathrm{15x}_{\mathrm{0}} ^{\mathrm{2}} −\mathrm{125}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{2x}_{\mathrm{0}} ^{\mathrm{3}} −\mathrm{15x}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{125}=\mathrm{0}\Leftrightarrow\left(\mathrm{x}_{\mathrm{0}} −\mathrm{5}\right)^{\mathrm{2}} \left(\mathrm{2x}_{\mathrm{0}} +\mathrm{5}\right) \\ $$$$\Leftrightarrow\mathrm{x}_{\mathrm{0}} =\frac{−\mathrm{5}}{\mathrm{2}}\Rightarrow\mathrm{y}'\left(\mathrm{x}_{\mathrm{0}} \right)=\mathrm{3}.\left(\frac{−\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{21}=\frac{−\mathrm{9}}{\mathrm{4}} \\ $$$$\left(\mathrm{2}\right)\Leftrightarrow−\mathrm{3x}_{\mathrm{1}} ^{\mathrm{3}} −\mathrm{12x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{21x}_{\mathrm{1}} +\mathrm{84}+\mathrm{x}_{\mathrm{1}} ^{\mathrm{3}} −\mathrm{21x}_{\mathrm{1}} −\mathrm{20} \\ $$$$\Leftrightarrow\mathrm{2x}_{\mathrm{1}} ^{\mathrm{3}} +\mathrm{12x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{64}=\mathrm{0}\Leftrightarrow\mathrm{x}_{\mathrm{1}} ^{\mathrm{3}} +\mathrm{6x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{32}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{x}_{\mathrm{1}} +\mathrm{4}\right)^{\mathrm{2}} \left(\mathrm{x}_{\mathrm{1}} −\mathrm{2}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}_{\mathrm{1}} =\mathrm{2}\Rightarrow\mathrm{y}'\left(\mathrm{2}\right)=−\mathrm{9} \\ $$$$\mathrm{Therefore},\mathrm{we}\:\mathrm{have}: \\ $$$$\left(\mathrm{d}_{\mathrm{1}} \right):\mathrm{y}=\frac{−\mathrm{9}}{\mathrm{4}}\mathrm{x}+\frac{\mathrm{135}}{\mathrm{8}} \\ $$$$\left(\mathrm{d}_{\mathrm{2}} \right):\mathrm{y}=−\mathrm{9x}−\mathrm{54} \\ $$$$\mathrm{P}=\left(\mathrm{d}_{\mathrm{1}} \right)\cap\left(\mathrm{d}_{\mathrm{2}} \right)\Rightarrow\mathrm{the}\:\mathrm{coordinates}\:\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\mathrm{of}\:\mathrm{P}\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{system}: \\ $$$$\begin{cases}{\mathrm{y}=\frac{−\mathrm{9x}}{\mathrm{4}}+\frac{\mathrm{135}}{\mathrm{8}}}\\{\mathrm{y}=−\mathrm{9x}−\mathrm{54}}\end{cases}\Leftrightarrow\begin{cases}{\mathrm{x}=\frac{−\mathrm{21}}{\mathrm{2}}}\\{\frac{\mathrm{81}}{\mathrm{2}}}\end{cases} \\ $$$$\mathrm{Thus},\mathrm{we}\:\mathrm{find}\:\mathrm{out}\:\mathrm{P}\left(\frac{−\mathrm{21}}{\mathrm{2}};\frac{\mathrm{81}}{\mathrm{2}}\right) \\ $$
Commented by ajfour last updated on 24/Aug/20
Thanks for your method Sir, i think your finally obtained eqs. of lines are not correct, please check..
$${Thanks}\:{for}\:{your}\:{method}\:{Sir},\:{i} \\ $$$${think}\:{your}\:{finally}\:{obtained}\:{eqs}. \\ $$$${of}\:{lines}\:{are}\:{not}\:{correct},\:{please} \\ $$$${check}.. \\ $$
Commented by 1549442205PVT last updated on 25/Aug/20
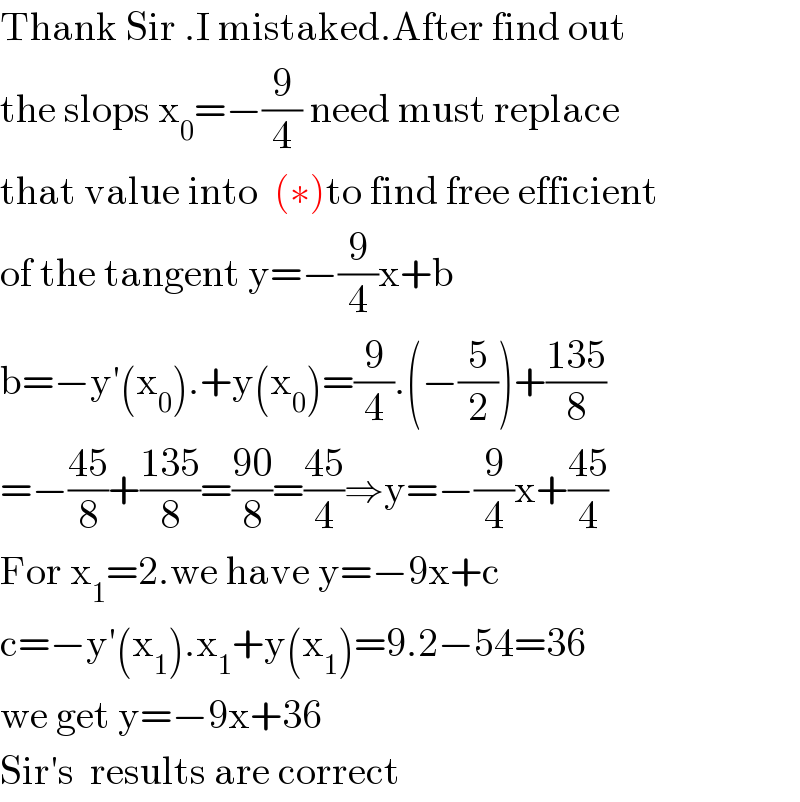
Thank Sir .I mistaked.After find out the slops x_0 =−(9/4) need must replace that value into (∗)to find free efficient of the tangent y=−(9/4)x+b b=−y′(x_0 ).+y(x_0 )=(9/4).(−(5/2))+((135)/8) =−((45)/8)+((135)/8)=((90)/8)=((45)/4)⇒y=−(9/4)x+((45)/4) For x_1 =2.we have y=−9x+c c=−y′(x_1 ).x_1 +y(x_1 )=9.2−54=36 we get y=−9x+36 Sir′s results are correct
$$\mathrm{Thank}\:\mathrm{Sir}\:.\mathrm{I}\:\mathrm{mistaked}.\mathrm{After}\:\mathrm{find}\:\mathrm{out} \\ $$$$\mathrm{the}\:\mathrm{slops}\:\mathrm{x}_{\mathrm{0}} =−\frac{\mathrm{9}}{\mathrm{4}}\:\mathrm{need}\:\mathrm{must}\:\mathrm{replace} \\ $$$$\mathrm{that}\:\mathrm{value}\:\mathrm{into}\:\:\left(\ast\right)\mathrm{to}\:\mathrm{find}\:\mathrm{free}\:\mathrm{efficient} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{tangent}\:\mathrm{y}=−\frac{\mathrm{9}}{\mathrm{4}}\mathrm{x}+\mathrm{b} \\ $$$$\mathrm{b}=−\mathrm{y}'\left(\mathrm{x}_{\mathrm{0}} \right).+\mathrm{y}\left(\mathrm{x}_{\mathrm{0}} \right)=\frac{\mathrm{9}}{\mathrm{4}}.\left(−\frac{\mathrm{5}}{\mathrm{2}}\right)+\frac{\mathrm{135}}{\mathrm{8}} \\ $$$$=−\frac{\mathrm{45}}{\mathrm{8}}+\frac{\mathrm{135}}{\mathrm{8}}=\frac{\mathrm{90}}{\mathrm{8}}=\frac{\mathrm{45}}{\mathrm{4}}\Rightarrow\mathrm{y}=−\frac{\mathrm{9}}{\mathrm{4}}\mathrm{x}+\frac{\mathrm{45}}{\mathrm{4}} \\ $$$$\mathrm{For}\:\mathrm{x}_{\mathrm{1}} =\mathrm{2}.\mathrm{we}\:\mathrm{have}\:\mathrm{y}=−\mathrm{9x}+\mathrm{c} \\ $$$$\mathrm{c}=−\mathrm{y}'\left(\mathrm{x}_{\mathrm{1}} \right).\mathrm{x}_{\mathrm{1}} +\mathrm{y}\left(\mathrm{x}_{\mathrm{1}} \right)=\mathrm{9}.\mathrm{2}−\mathrm{54}=\mathrm{36} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{y}=−\mathrm{9x}+\mathrm{36} \\ $$$$\mathrm{Sir}'\mathrm{s}\:\:\mathrm{results}\:\mathrm{are}\:\mathrm{correct} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *