Question Number 109493 by bemath last updated on 24/Aug/20

Answered by Dwaipayan Shikari last updated on 24/Aug/20
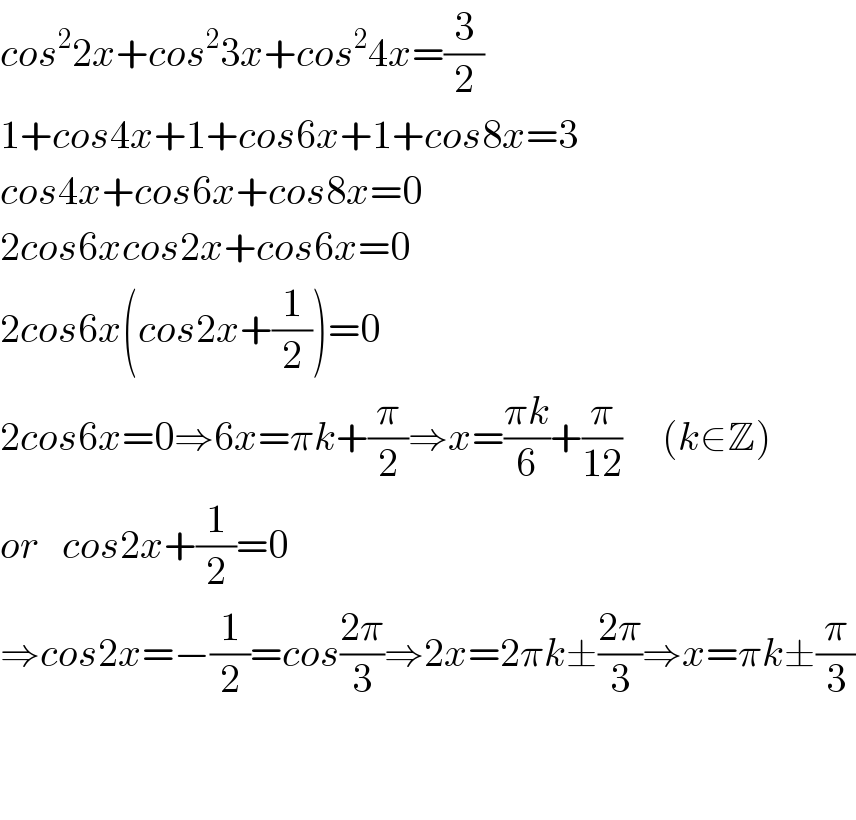
$${cos}^{\mathrm{2}} \mathrm{2}{x}+{cos}^{\mathrm{2}} \mathrm{3}{x}+{cos}^{\mathrm{2}} \mathrm{4}{x}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{1}+{cos}\mathrm{4}{x}+\mathrm{1}+{cos}\mathrm{6}{x}+\mathrm{1}+{cos}\mathrm{8}{x}=\mathrm{3} \\ $$$${cos}\mathrm{4}{x}+{cos}\mathrm{6}{x}+{cos}\mathrm{8}{x}=\mathrm{0} \\ $$$$\mathrm{2}{cos}\mathrm{6}{xcos}\mathrm{2}{x}+{cos}\mathrm{6}{x}=\mathrm{0} \\ $$$$\mathrm{2}{cos}\mathrm{6}{x}\left({cos}\mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\mathrm{2}{cos}\mathrm{6}{x}=\mathrm{0}\Rightarrow\mathrm{6}{x}=\pi{k}+\frac{\pi}{\mathrm{2}}\Rightarrow{x}=\frac{\pi{k}}{\mathrm{6}}+\frac{\pi}{\mathrm{12}}\:\:\:\:\:\left({k}\in\mathbb{Z}\right) \\ $$$${or}\:\:\:{cos}\mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow{cos}\mathrm{2}{x}=−\frac{\mathrm{1}}{\mathrm{2}}={cos}\frac{\mathrm{2}\pi}{\mathrm{3}}\Rightarrow\mathrm{2}{x}=\mathrm{2}\pi{k}\pm\frac{\mathrm{2}\pi}{\mathrm{3}}\Rightarrow{x}=\pi{k}\pm\frac{\pi}{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$
