Question Number 109494 by mathdave last updated on 24/Aug/20
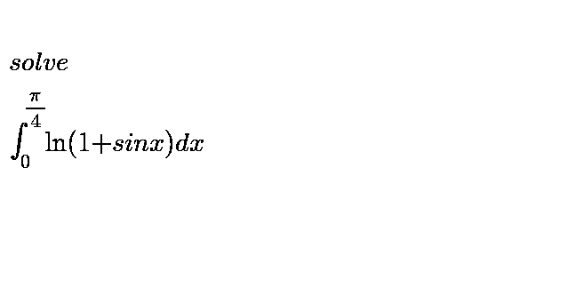
Answered by mathmax by abdo last updated on 24/Aug/20
![for ∣u∣<1 we have (d/du)ln(1+u) =(1/(1+u)) =Σ_(n=0) ^∞ (−1)^n u^n ⇒ ln(1+u) =Σ_(n=0) ^∞ (((−1)^n )/(n+1))u^(n+1) +c (c=0) =Σ_(n=1) ^∞ (((−1)^(n−1) u^n )/n) ⇒ ∫_0 ^(π/4) ln(1+sinx)dx =∫_0 ^(π/4) Σ_(n=1) ^∞ (((−1)^n )/n) sin^n xdx =Σ_(n=1) ^∞ (((−1)^n )/n) ∫_0 ^(π/4) sin^n x dx let A_n =∫_0 ^(π/4) sin^n xdx (wallis integral on[0,(π/4)]) ⇒A_n =∫_0 ^(π/4) (((e^(ix) −e^(−ix) )/(2i)))^n dx =(1/((2i)^n )) ∫_0 ^(π/4) Σ_(k=0) ^n C_n ^k (e^(ix) )^k (e^(−ix) )^((n−k)) =(1/((2i)^n )) Σ_(k=0) ^n C_n ^k ∫_0 ^(π/4) e^(ikx) e^(−i(n−k)x) dx =(1/((2i)^n )) Σ_(k=0) ^n C_n ^k ∫_0 ^(π/4) e^(i(2k−n)x) dx =(1/((2i))) Σ_(k=0) ^n C_n ^k [(1/(i(2k−n))) e^(i(2k−n)x) ]_0 ^(π/4) =....be continued...](https://www.tinkutara.com/question/Q109571.png)
$$\mathrm{for}\:\mid\mathrm{u}\mid<\mathrm{1}\:\:\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{d}}{\mathrm{du}}\mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{n}} \:\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\mathrm{u}^{\mathrm{n}+\mathrm{1}} \:+\mathrm{c}\:\left(\mathrm{c}=\mathrm{0}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{u}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{sinx}\right)\mathrm{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}}\:\mathrm{sin}^{\mathrm{n}} \mathrm{xdx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{sin}^{\mathrm{n}} \mathrm{x}\:\mathrm{dx}\:\:\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{sin}^{\mathrm{n}} \:\mathrm{xdx} \\ $$$$\left(\mathrm{wallis}\:\mathrm{integral}\:\mathrm{on}\left[\mathrm{0},\frac{\pi}{\mathrm{4}}\right]\right)\:\Rightarrow\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\frac{\mathrm{e}^{\mathrm{ix}} −\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2i}}\right)^{\mathrm{n}} \mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{n}} }\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{k}} \left(\mathrm{e}^{−\mathrm{ix}} \right)^{\left(\mathrm{n}−\mathrm{k}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{e}^{\mathrm{ikx}} \:\mathrm{e}^{−\mathrm{i}\left(\mathrm{n}−\mathrm{k}\right)\mathrm{x}} \:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}} \mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2i}\right)}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left[\frac{\mathrm{1}}{\mathrm{i}\left(\mathrm{2k}−\mathrm{n}\right)}\:\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}} \right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:=….\mathrm{be}\:\mathrm{continued}… \\ $$
Answered by mathmax by abdo last updated on 25/Aug/20
![let try another way I =∫_0 ^(π/4) ln(cos^2 ((x/2))+sin^2 ((x/2))+2cos((x/2))sin((x/2))dx =∫_0 ^(π/4) ln{(cos((x/2))+sin((x/2))^2 )dx =2∫_0 ^(π/4) ln(cos((x/2))+sin((x/2)))dx =_((x/2)=t) 2 ∫_0 ^(π/8) ln(cost +sint)dt let f(a) =∫_0 ^(π/8) ln(cost +asint)dt f^′ (a) =∫_0 ^(π/8) ((sint)/(cost +a sint)) dt =∫_0 ^(π/8) (dt/(a+(1/(tant)))) =_(tant =u) ∫_0 ^((√2)−1) (du/((1+u^2 )(a+(1/u)))) =∫_0 ^((√2)−1) ((udu)/((au+1)(u^2 +1))) let decompose F(u) =(u/((au+1)(u^2 +1))) F(u) =(x/(au+1)) +((yu +z)/(u^2 +1)) ⇒x =((−1)/(a((1/a^2 )+1))) =((−1)/((1/a) +a)) =((−1)/(1+a^2 )) lim_(u→+∞) uF(u) =0 =(x/a) +y ⇒y =−(x/a) =(1/(a(1+a^2 ))) F(0) =0 =x +z ⇒z =−x =(1/(1+a^2 )) ⇒ F(u) =((−1)/((1+a^2 )(au+1))) +(((1/(a(1+a^2 )))u+(1/(1+a^2 )))/(u^2 +1)) =(1/(1+a^2 )){((−1)/(au+1)) +(1/a) (u/(u^2 +1)) +(1/(u^2 +1))} ⇒∫_0 ^((√2)−1) F(u)du =−(1/(1+a^2 ))∫_0 ^((√2)−1) (du/(au +1)) +(1/(2a(1+a^2 )))∫_0 ^((√2)−1) ((2udu)/(u^2 +1)) +(1/(1+a^2 ))∫_0 ^((√2)−1) (du/(1+a^2 )) =−(1/(a(1+a^2 )))[ln(au+1)]_0 ^((√2)−1) +(1/(2a(1+a^2 )))[ln(1+u^2 )]_0 ^((√2)−1) +(1/(1+a^2 ))arctan((√2)−1) =−((ln(a((√2)−1)+1))/(a(1+a^2 ))) +((ln(1+((√2)−1)^2 ))/(2a(1+a^2 ))) +(π/(8(1+a^2 ))) ⇒ ⇒f(a) =−∫ ((ln(a((√2)−1)+1))/(a(1+a^2 )))da +((ln(4−2(√2)))/2)arctana +(π/8) arctan(a) +C =−∫ ((ln(1+((√2)−1)a))/(a(1+a^2 )))da +((π/8) +((ln(4−2(√2)))/2))arctan(a) +C rest calculus of ∫ ((ln(1+((√2)−1)a))/(a(1+a^2 )))da....be continued...](https://www.tinkutara.com/question/Q109703.png)
$$\mathrm{let}\:\mathrm{try}\:\mathrm{another}\:\mathrm{way}\:\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{cos}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{sin}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{2cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{dx}\right. \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left\{\left(\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} \right)\mathrm{dx}\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)\mathrm{dx}\right. \\ $$$$=_{\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{t}} \:\:\:\:\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{8}}} \:\mathrm{ln}\left(\mathrm{cost}\:+\mathrm{sint}\right)\mathrm{dt}\:\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{8}}} \:\mathrm{ln}\left(\mathrm{cost}\:+\mathrm{asint}\right)\mathrm{dt} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{8}}} \:\frac{\mathrm{sint}}{\mathrm{cost}\:+\mathrm{a}\:\mathrm{sint}}\:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{8}}} \:\:\:\frac{\mathrm{dt}}{\mathrm{a}+\frac{\mathrm{1}}{\mathrm{tant}}}\:=_{\mathrm{tant}\:=\mathrm{u}} \:\:\:\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\mathrm{a}+\frac{\mathrm{1}}{\mathrm{u}}\right)} \\ $$$$=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{\mathrm{udu}}{\left(\mathrm{au}+\mathrm{1}\right)\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\mathrm{u}}{\left(\mathrm{au}+\mathrm{1}\right)\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\mathrm{x}}{\mathrm{au}+\mathrm{1}}\:+\frac{\mathrm{yu}\:+\mathrm{z}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\mathrm{x}\:=\frac{−\mathrm{1}}{\mathrm{a}\left(\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }+\mathrm{1}\right)}\:=\frac{−\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{a}}\:+\mathrm{a}}\:=\frac{−\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{lim}_{\mathrm{u}\rightarrow+\infty} \mathrm{uF}\left(\mathrm{u}\right)\:=\mathrm{0}\:=\frac{\mathrm{x}}{\mathrm{a}}\:+\mathrm{y}\:\Rightarrow\mathrm{y}\:=−\frac{\mathrm{x}}{\mathrm{a}}\:=\frac{\mathrm{1}}{\mathrm{a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)} \\ $$$$\mathrm{F}\left(\mathrm{0}\right)\:=\mathrm{0}\:=\mathrm{x}\:+\mathrm{z}\:\Rightarrow\mathrm{z}\:=−\mathrm{x}\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{u}\right)\:=\frac{−\mathrm{1}}{\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)\left(\mathrm{au}+\mathrm{1}\right)}\:+\frac{\frac{\mathrm{1}}{\mathrm{a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\mathrm{u}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\left\{\frac{−\mathrm{1}}{\mathrm{au}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{a}}\:\frac{\mathrm{u}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\right\}\:\Rightarrow\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\mathrm{F}\left(\mathrm{u}\right)\mathrm{du} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{du}}{\mathrm{au}\:+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{2udu}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\left[\mathrm{ln}\left(\mathrm{au}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{2a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\left[\mathrm{ln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\mathrm{arctan}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$=−\frac{\mathrm{ln}\left(\mathrm{a}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)+\mathrm{1}\right)}{\mathrm{a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\:+\frac{\mathrm{ln}\left(\mathrm{1}+\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} \right)}{\mathrm{2a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\:+\frac{\pi}{\mathrm{8}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\:\Rightarrow \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=−\int\:\:\frac{\mathrm{ln}\left(\mathrm{a}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)+\mathrm{1}\right)}{\mathrm{a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\mathrm{da}\:+\frac{\mathrm{ln}\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right)}{\mathrm{2}}\mathrm{arctana}\:+\frac{\pi}{\mathrm{8}}\:\mathrm{arctan}\left(\mathrm{a}\right)\:+\mathrm{C} \\ $$$$=−\int\:\frac{\mathrm{ln}\left(\mathrm{1}+\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\mathrm{a}\right)}{\mathrm{a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\mathrm{da}\:+\left(\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{ln}\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right)}{\mathrm{2}}\right)\mathrm{arctan}\left(\mathrm{a}\right)\:+\mathrm{C} \\ $$$$\mathrm{rest}\:\mathrm{calculus}\:\mathrm{of}\:\int\:\frac{\mathrm{ln}\left(\mathrm{1}+\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\mathrm{a}\right)}{\mathrm{a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\mathrm{da}….\mathrm{be}\:\mathrm{continued}… \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 25/Aug/20
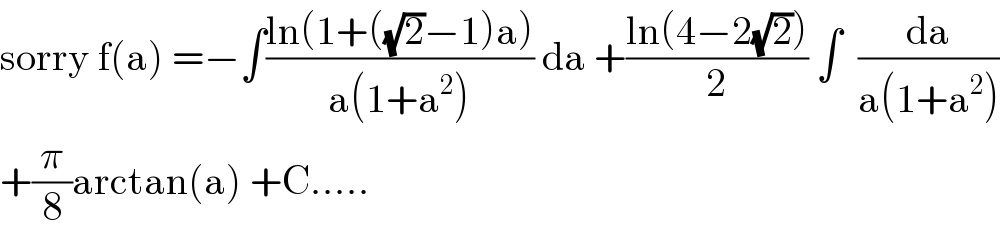
$$\mathrm{sorry}\:\mathrm{f}\left(\mathrm{a}\right)\:=−\int\frac{\mathrm{ln}\left(\mathrm{1}+\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\mathrm{a}\right)}{\mathrm{a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\:\mathrm{da}\:+\frac{\mathrm{ln}\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right)}{\mathrm{2}}\:\int\:\:\frac{\mathrm{da}}{\mathrm{a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)} \\ $$$$+\frac{\pi}{\mathrm{8}}\mathrm{arctan}\left(\mathrm{a}\right)\:+\mathrm{C}….. \\ $$
