Question-109540

Question Number 109540 by ajfour last updated on 24/Aug/20

Commented by ajfour last updated on 24/Aug/20

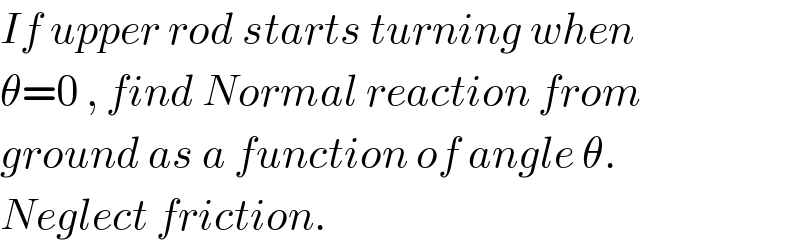
If upper rod starts turning when θ=0 , find Normal reaction from ground as a function of angle θ. Neglect friction.

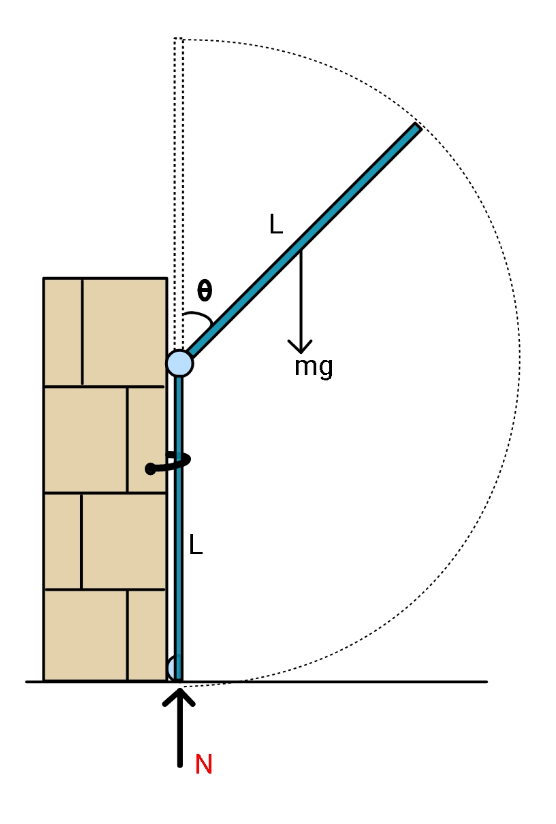
$${If}\:{upper}\:{rod}\:{starts}\:{turning}\:{when} \\ $$$$\theta=\mathrm{0}\:,\:{find}\:{Normal}\:{reaction}\:{from} \\ $$$${ground}\:{as}\:{a}\:{function}\:{of}\:{angle}\:\theta. \\ $$$${Neglect}\:{friction}. \\ $$

Answered by mr W last updated on 25/Aug/20

mg ((l sin θ)/2)=((ml^2 )/3)α ⇒α=((3g sin θ)/(2l)) ⇒ω(dω/dθ)=((3g sin θ)/(2l)) ⇒(ω^2 /2)=((3g(1−cos θ))/(2l)) ⇒ω^2 =((3g(1−cos θ))/l) mg+mg−N=m ((lα)/2)sin θ+(l/2)mω^2 cos θ 2mg−N=((3mg sin^2 θ)/4)+((mg(6 cos θ−6 cos^2 θ))/4) ⇒N=mg[2− ((3(1−cos θ)(1+3 cos θ))/4)]

$${mg}\:\frac{{l}\:\mathrm{sin}\:\theta}{\mathrm{2}}=\frac{{ml}^{\mathrm{2}} }{\mathrm{3}}\alpha \\ $$$$\Rightarrow\alpha=\frac{\mathrm{3}{g}\:\mathrm{sin}\:\theta}{\mathrm{2}{l}} \\ $$$$\Rightarrow\omega\frac{{d}\omega}{{d}\theta}=\frac{\mathrm{3}{g}\:\mathrm{sin}\:\theta}{\mathrm{2}{l}} \\ $$$$\Rightarrow\frac{\omega^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{3}{g}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}{\mathrm{2}{l}} \\ $$$$\Rightarrow\omega^{\mathrm{2}} =\frac{\mathrm{3}{g}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}{{l}} \\ $$$${mg}+{mg}−{N}={m}\:\frac{{l}\alpha}{\mathrm{2}}\mathrm{sin}\:\theta+\frac{{l}}{\mathrm{2}}{m}\omega^{\mathrm{2}} \mathrm{cos}\:\theta \\ $$$$\mathrm{2}{mg}−{N}=\frac{\mathrm{3}{mg}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{4}}+\frac{{mg}\left(\mathrm{6}\:\mathrm{cos}\:\theta−\mathrm{6}\:\mathrm{cos}^{\mathrm{2}} \:\theta\right)}{\mathrm{4}} \\ $$$$\Rightarrow{N}={mg}\left[\mathrm{2}−\:\frac{\mathrm{3}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\left(\mathrm{1}+\mathrm{3}\:\mathrm{cos}\:\theta\right)}{\mathrm{4}}\right] \\ $$

Commented by mr W last updated on 24/Aug/20