Menu Close

Question-109611

Tinku Tara 0 Comments
Pin




Question Number 109611 by mnjuly1970 last updated on 24/Aug/20
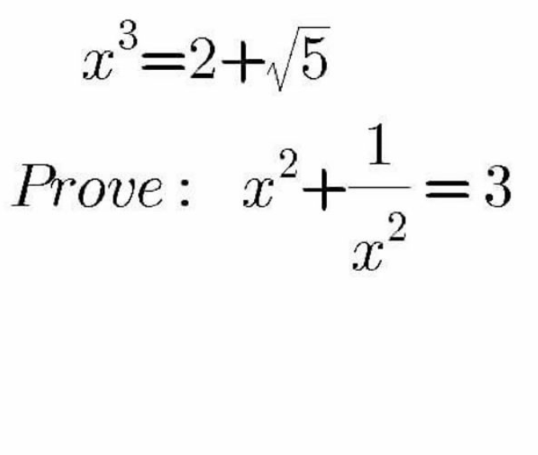
Commented by Rasheed.Sindhi last updated on 25/Aug/20
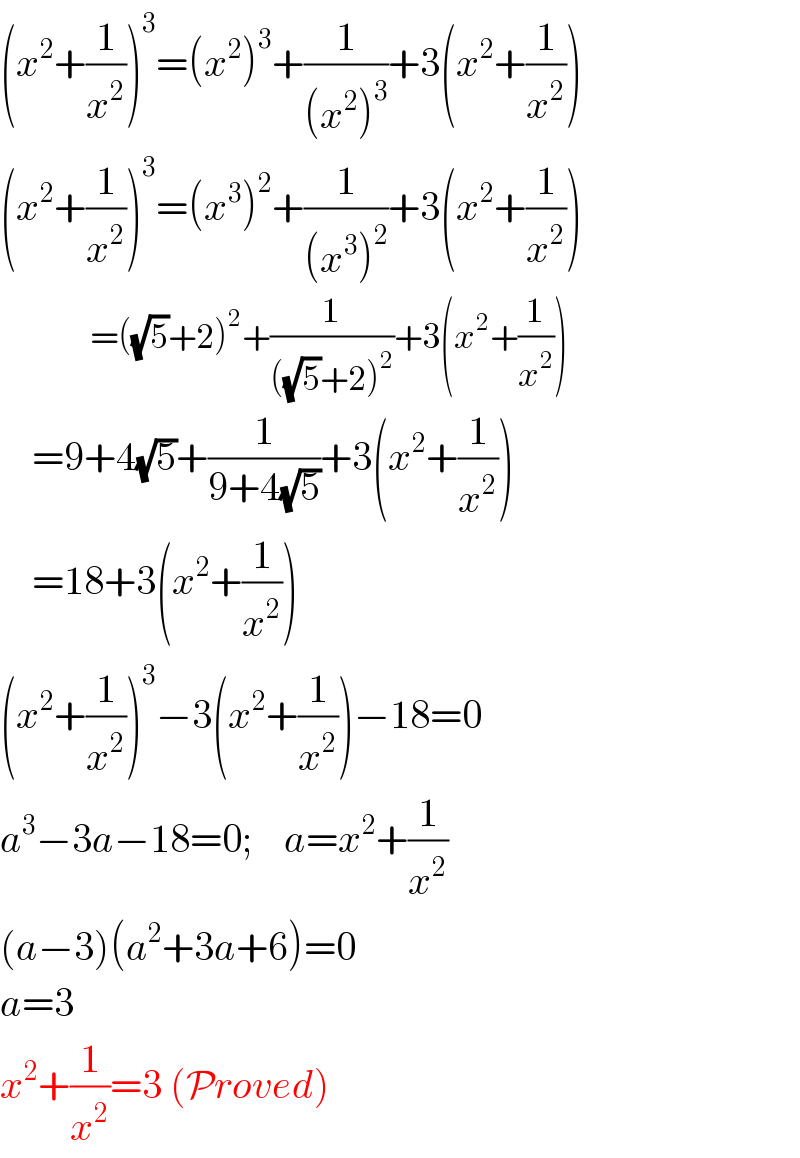
(x^2 +(1/x^2 ))^3 =(x^2 )^3 +(1/((x^2 )^3 ))+3(x^2 +(1/x^2 )) (x^2 +(1/x^2 ))^3 =(x^3 )^2 +(1/((x^3 )^2 ))+3(x^2 +(1/x^2 )) =((√5)+2)^2 +(1/(((√5)+2)^2 ))+3(x^2 +(1/x^2 )) =9+4(√5)+(1/(9+4(√5)))+3(x^2 +(1/x^2 )) =18+3(x^2 +(1/x^2 )) (x^2 +(1/x^2 ))^3 −3(x^2 +(1/x^2 ))−18=0 a^3 −3a−18=0; a=x^2 +(1/x^2 ) (a−3)(a^2 +3a+6)=0 a=3 x^2 +(1/x^2 )=3 (Proved)
$$\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{3}} =\left({x}^{\mathrm{2}} \right)^{\mathrm{3}} +\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} \right)^{\mathrm{3}} }+\mathrm{3}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$$\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{3}} =\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} +\frac{\mathrm{1}}{\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} }+\mathrm{3}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\sqrt{\mathrm{5}}+\mathrm{2}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\left(\sqrt{\mathrm{5}}+\mathrm{2}\right)^{\mathrm{2}} }+\mathrm{3}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:=\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}}}+\mathrm{3}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:=\mathrm{18}+\mathrm{3}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$$\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{3}} −\mathrm{3}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)−\mathrm{18}=\mathrm{0} \\ $$$${a}^{\mathrm{3}} −\mathrm{3}{a}−\mathrm{18}=\mathrm{0};\:\:\:\:{a}={x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$$\left({a}−\mathrm{3}\right)\left({a}^{\mathrm{2}} +\mathrm{3}{a}+\mathrm{6}\right)=\mathrm{0} \\ $$$${a}=\mathrm{3} \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{3}\:\left(\mathcal{P}{roved}\right) \\ $$
Answered by ajfour last updated on 25/Aug/20
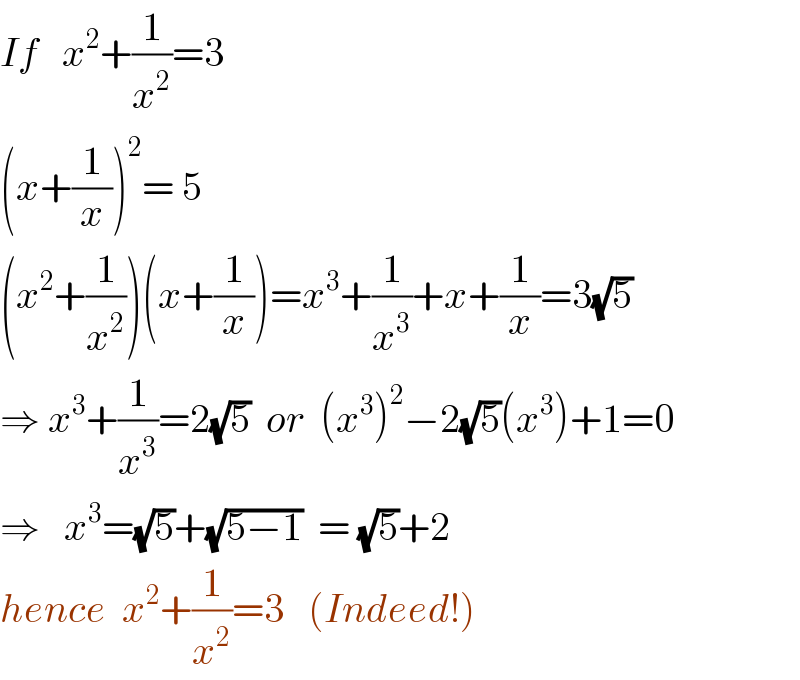
If x^2 +(1/x^2 )=3 (^() x+(1/x))^2 = 5 (x^2 +(1/x^2 ))(x+(1/x))=x^3 +(1/x^3 )+x+(1/x)=3(√5) ⇒ x^3 +(1/x^3 )=2(√5) or (x^3 )^2 −2(√5)(x^3 )+1=0 ⇒ x^3 =(√5)+(√(5−1)) = (√5)+2 hence x^2 +(1/x^2 )=3 (Indeed!)
$${If}\:\:\:{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{3} \\ $$$$\left(^{} {x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} =\:\mathrm{5} \\ $$$$\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\left({x}+\frac{\mathrm{1}}{{x}}\right)={x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }+{x}+\frac{\mathrm{1}}{{x}}=\mathrm{3}\sqrt{\mathrm{5}} \\ $$$$\Rightarrow\:{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\mathrm{2}\sqrt{\mathrm{5}}\:\:{or}\:\:\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{5}}\left({x}^{\mathrm{3}} \right)+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{x}^{\mathrm{3}} =\sqrt{\mathrm{5}}+\sqrt{\mathrm{5}−\mathrm{1}}\:\:=\:\sqrt{\mathrm{5}}+\mathrm{2} \\ $$$${hence}\:\:{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{3}\:\:\:\left({Indeed}!\right) \\ $$
Answered by Her_Majesty last updated on 24/Aug/20
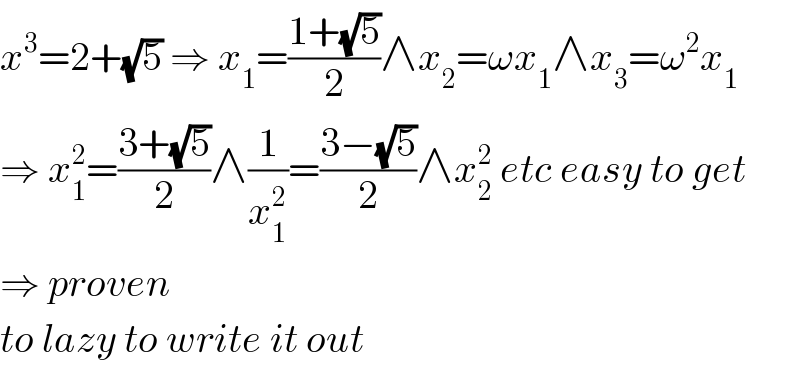
x^3 =2+(√5) ⇒ x_1 =((1+(√5))/2)∧x_2 =ωx_1 ∧x_3 =ω^2 x_1 ⇒ x_1 ^2 =((3+(√5))/2)∧(1/x_1 ^2 )=((3−(√5))/2)∧x_2 ^2 etc easy to get ⇒ proven to lazy to write it out
$${x}^{\mathrm{3}} =\mathrm{2}+\sqrt{\mathrm{5}}\:\Rightarrow\:{x}_{\mathrm{1}} =\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\wedge{x}_{\mathrm{2}} =\omega{x}_{\mathrm{1}} \wedge{x}_{\mathrm{3}} =\omega^{\mathrm{2}} {x}_{\mathrm{1}} \\ $$$$\Rightarrow\:{x}_{\mathrm{1}} ^{\mathrm{2}} =\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}}\wedge\frac{\mathrm{1}}{{x}_{\mathrm{1}} ^{\mathrm{2}} }=\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}}\wedge{x}_{\mathrm{2}} ^{\mathrm{2}} \:{etc}\:{easy}\:{to}\:{get} \\ $$$$\Rightarrow\:{proven} \\ $$$${to}\:{lazy}\:{to}\:{write}\:{it}\:{out} \\ $$
Answered by Rasheed.Sindhi last updated on 24/Aug/20
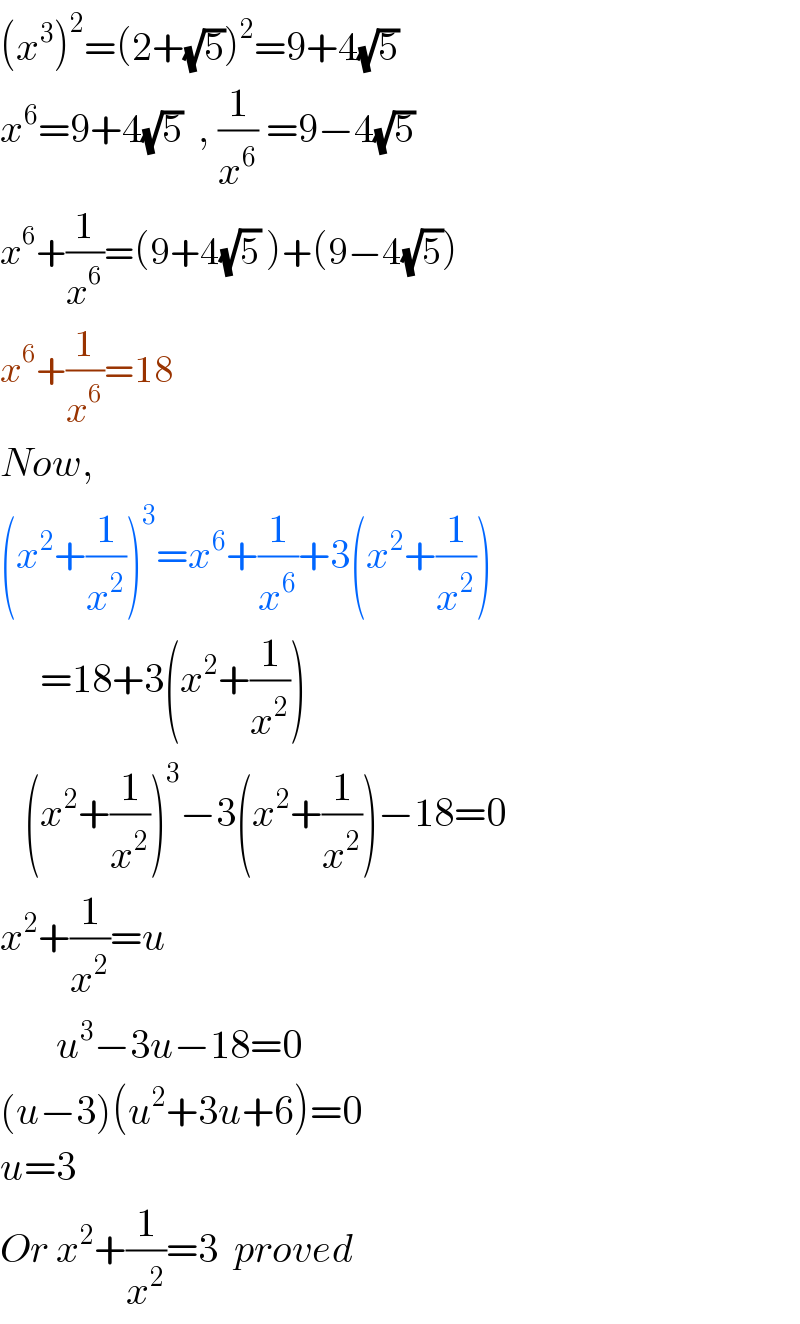
(x^3 )^2 =(2+(√5))^2 =9+4(√5) x^6 =9+4(√5) , (1/x^6 ) =9−4(√5) x^6 +(1/x^6 )=(9+4(√5) )+(9−4(√5)) x^6 +(1/x^6 )=18 Now, (x^2 +(1/x^2 ))^3 =x^6 +(1/x^6 )+3(x^2 +(1/x^2 )) =18+3(x^2 +(1/x^2 )) (x^2 +(1/x^2 ))^3 −3(x^2 +(1/x^2 ))−18=0 x^2 +(1/x^2 )=u u^3 −3u−18=0 (u−3)(u^2 +3u+6)=0 u=3 Or x^2 +(1/x^2 )=3 proved
$$\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} =\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} =\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}} \\ $$$${x}^{\mathrm{6}} =\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}}\:\:,\:\frac{\mathrm{1}}{{x}^{\mathrm{6}} }\:=\mathrm{9}−\mathrm{4}\sqrt{\mathrm{5}} \\ $$$${x}^{\mathrm{6}} +\frac{\mathrm{1}}{{x}^{\mathrm{6}} }=\left(\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}}\:\right)+\left(\mathrm{9}−\mathrm{4}\sqrt{\mathrm{5}}\right) \\ $$$${x}^{\mathrm{6}} +\frac{\mathrm{1}}{{x}^{\mathrm{6}} }=\mathrm{18} \\ $$$${Now}, \\ $$$$\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{3}} ={x}^{\mathrm{6}} +\frac{\mathrm{1}}{{x}^{\mathrm{6}} }+\mathrm{3}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:=\mathrm{18}+\mathrm{3}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{3}} −\mathrm{3}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)−\mathrm{18}=\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }={u} \\ $$$$\:\:\:\:\:\:\:{u}^{\mathrm{3}} −\mathrm{3}{u}−\mathrm{18}=\mathrm{0} \\ $$$$\left({u}−\mathrm{3}\right)\left({u}^{\mathrm{2}} +\mathrm{3}{u}+\mathrm{6}\right)=\mathrm{0} \\ $$$${u}=\mathrm{3} \\ $$$${Or}\:{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{3}\:\:{proved} \\ $$
Commented by mnjuly1970 last updated on 24/Aug/20
thank you sir..
$${thank}\:{you}\:{sir}.. \\ $$
Answered by 1549442205PVT last updated on 25/Aug/20
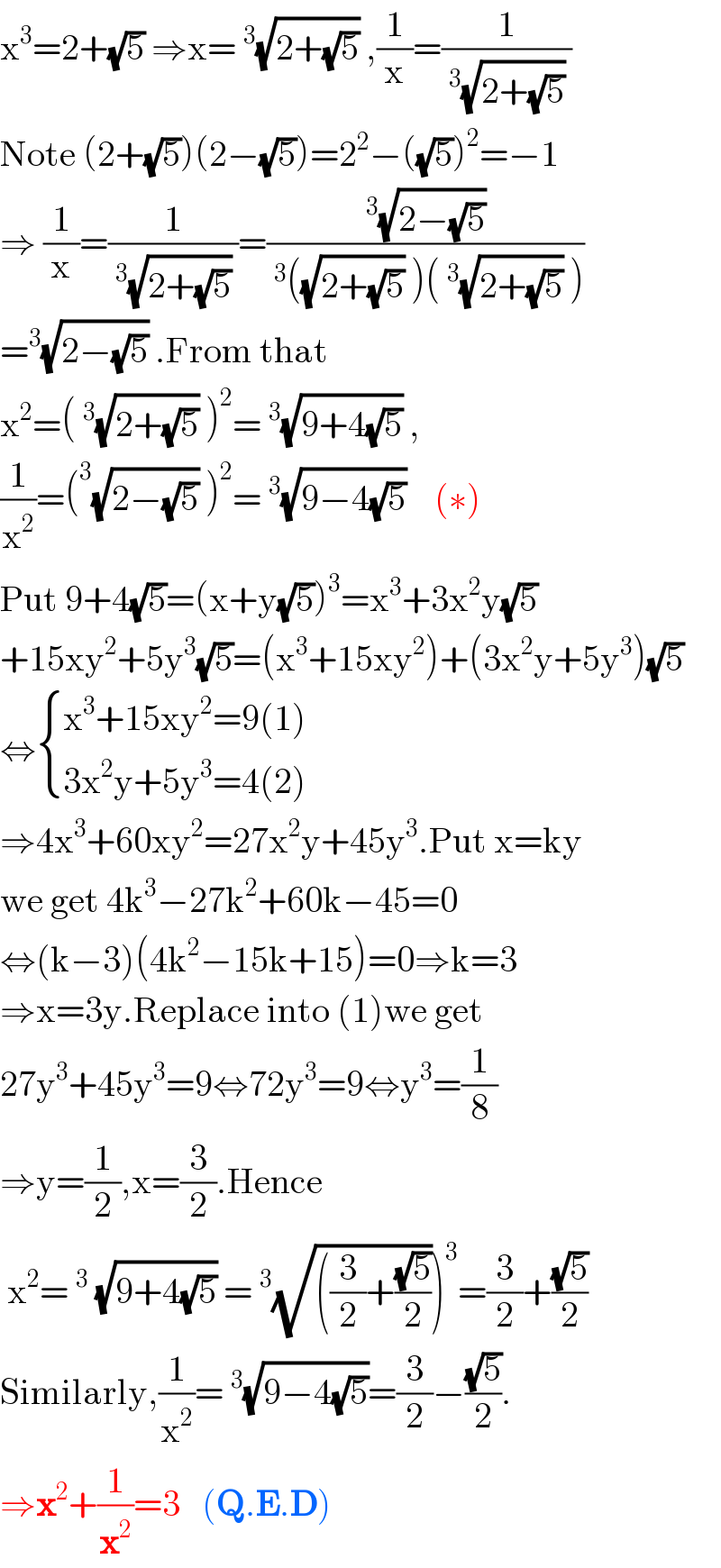
x^3 =2+(√5) ⇒x=^3 (√(2+(√5))) ,(1/x)=(1/(^3 (√(2+(√5))) )) Note (2+(√5))(2−(√5))=2^2 −((√5))^2 =−1 ⇒ (1/x)=(1/(^3 (√(2+(√5))) ))=((^3 (√(2−(√5))) )/(^3 ((√(2+(√5))) )(^3 (√(2+(√5))) ))) =^3 (√(2−(√5))) .From that x^2 =(^3 (√(2+(√5))) )^2 =^3 (√(9+4(√5))) , (1/x^2 )=(^3 (√(2−(√5))) )^2 =^3 (√(9−4(√5))) (∗) Put 9+4(√5)=(x+y(√5))^3 =x^3 +3x^2 y(√5) +15xy^2 +5y^3 (√5)=(x^3 +15xy^2 )+(3x^2 y+5y^3 )(√5) ⇔ { ((x^3 +15xy^2 =9(1))),((3x^2 y+5y^3 =4(2))) :} ⇒4x^3 +60xy^2 =27x^2 y+45y^3 .Put x=ky we get 4k^3 −27k^2 +60k−45=0 ⇔(k−3)(4k^2 −15k+15)=0⇒k=3 ⇒x=3y.Replace into (1)we get 27y^3 +45y^3 =9⇔72y^3 =9⇔y^3 =(1/8) ⇒y=(1/2),x=(3/2).Hence x^2 =^3 (√(9+4(√5))) =^3 (√(((3/2)+((√5)/2))))^3 =(3/2)+((√5)/2) Similarly,(1/x^2 )=^3 (√(9−4(√5)))=(3/2)−((√5)/2). ⇒x^2 +(1/x^2 )=3 (Q.E.D)
$$\mathrm{x}^{\mathrm{3}} =\mathrm{2}+\sqrt{\mathrm{5}}\:\Rightarrow\mathrm{x}=\:^{\mathrm{3}} \sqrt{\mathrm{2}+\sqrt{\mathrm{5}}}\:,\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{1}}{\:^{\mathrm{3}} \sqrt{\mathrm{2}+\sqrt{\mathrm{5}}}\:} \\ $$$$\mathrm{Note}\:\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)\left(\mathrm{2}−\sqrt{\mathrm{5}}\right)=\mathrm{2}^{\mathrm{2}} −\left(\sqrt{\mathrm{5}}\right)^{\mathrm{2}} =−\mathrm{1} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{1}}{\:^{\mathrm{3}} \sqrt{\mathrm{2}+\sqrt{\mathrm{5}}}\:}=\frac{\:^{\mathrm{3}} \sqrt{\mathrm{2}−\sqrt{\mathrm{5}}}\:}{\:^{\mathrm{3}} \left(\sqrt{\mathrm{2}+\sqrt{\mathrm{5}}}\:\right)\left(\:^{\mathrm{3}} \sqrt{\mathrm{2}+\sqrt{\mathrm{5}}}\:\right)} \\ $$$$=^{\mathrm{3}} \sqrt{\mathrm{2}−\sqrt{\mathrm{5}}}\:.\mathrm{From}\:\mathrm{that} \\ $$$$\mathrm{x}^{\mathrm{2}} =\left(\:^{\mathrm{3}} \sqrt{\mathrm{2}+\sqrt{\mathrm{5}}}\:\right)^{\mathrm{2}} =\:^{\mathrm{3}} \sqrt{\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}}}\:, \\ $$$$\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\left(^{\mathrm{3}} \sqrt{\mathrm{2}−\sqrt{\mathrm{5}}}\:\right)^{\mathrm{2}} =\:^{\mathrm{3}} \sqrt{\mathrm{9}−\mathrm{4}\sqrt{\mathrm{5}}}\:\:\:\:\left(\ast\right) \\ $$$$\mathrm{Put}\:\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}}=\left(\mathrm{x}+\mathrm{y}\sqrt{\mathrm{5}}\right)^{\mathrm{3}} =\mathrm{x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} \mathrm{y}\sqrt{\mathrm{5}} \\ $$$$+\mathrm{15xy}^{\mathrm{2}} +\mathrm{5y}^{\mathrm{3}} \sqrt{\mathrm{5}}=\left(\mathrm{x}^{\mathrm{3}} +\mathrm{15xy}^{\mathrm{2}} \right)+\left(\mathrm{3x}^{\mathrm{2}} \mathrm{y}+\mathrm{5y}^{\mathrm{3}} \right)\sqrt{\mathrm{5}} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{x}^{\mathrm{3}} +\mathrm{15xy}^{\mathrm{2}} =\mathrm{9}\left(\mathrm{1}\right)}\\{\mathrm{3x}^{\mathrm{2}} \mathrm{y}+\mathrm{5y}^{\mathrm{3}} =\mathrm{4}\left(\mathrm{2}\right)}\end{cases} \\ $$$$\Rightarrow\mathrm{4x}^{\mathrm{3}} +\mathrm{60xy}^{\mathrm{2}} =\mathrm{27x}^{\mathrm{2}} \mathrm{y}+\mathrm{45y}^{\mathrm{3}} .\mathrm{Put}\:\mathrm{x}=\mathrm{ky} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{4k}^{\mathrm{3}} −\mathrm{27k}^{\mathrm{2}} +\mathrm{60k}−\mathrm{45}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{k}−\mathrm{3}\right)\left(\mathrm{4k}^{\mathrm{2}} −\mathrm{15k}+\mathrm{15}\right)=\mathrm{0}\Rightarrow\mathrm{k}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{3y}.\mathrm{Replace}\:\mathrm{into}\:\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{get}\: \\ $$$$\mathrm{27y}^{\mathrm{3}} +\mathrm{45y}^{\mathrm{3}} =\mathrm{9}\Leftrightarrow\mathrm{72y}^{\mathrm{3}} =\mathrm{9}\Leftrightarrow\mathrm{y}^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{1}}{\mathrm{2}},\mathrm{x}=\frac{\mathrm{3}}{\mathrm{2}}.\mathrm{Hence}\: \\ $$$$\left.\:\mathrm{x}^{\mathrm{2}} =\:^{\mathrm{3}} \:\sqrt{\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}}}\:=\:^{\mathrm{3}} \sqrt{\left(\frac{\mathrm{3}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right.}\right)^{\mathrm{3}} =\frac{\mathrm{3}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{Similarly},\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\:^{\mathrm{3}} \sqrt{\mathrm{9}−\mathrm{4}\sqrt{\mathrm{5}}}=\frac{\mathrm{3}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}. \\ $$$$\Rightarrow\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }=\mathrm{3}\:\:\:\left(\boldsymbol{\mathrm{Q}}.\boldsymbol{\mathrm{E}}.\boldsymbol{\mathrm{D}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *