Question-109626

Question Number 109626 by qwerty111 last updated on 24/Aug/20

Commented by kaivan.ahmadi last updated on 24/Aug/20

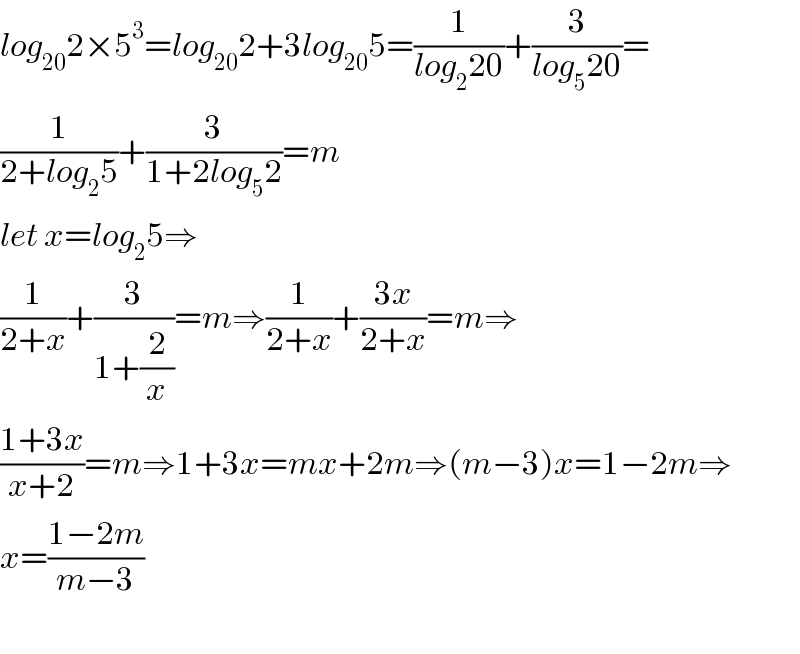
log_(20) 2×5^3 =log_(20) 2+3log_(20) 5=(1/(log_2 20))+(3/(log_5 20))= (1/(2+log_2 5))+(3/(1+2log_5 2))=m let x=log_2 5⇒ (1/(2+x))+(3/(1+(2/x)))=m⇒(1/(2+x))+((3x)/(2+x))=m⇒ ((1+3x)/(x+2))=m⇒1+3x=mx+2m⇒(m−3)x=1−2m⇒ x=((1−2m)/(m−3))

$${log}_{\mathrm{20}} \mathrm{2}×\mathrm{5}^{\mathrm{3}} ={log}_{\mathrm{20}} \mathrm{2}+\mathrm{3}{log}_{\mathrm{20}} \mathrm{5}=\frac{\mathrm{1}}{{log}_{\mathrm{2}} \mathrm{20}}+\frac{\mathrm{3}}{{log}_{\mathrm{5}} \mathrm{20}}= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}+{log}_{\mathrm{2}} \mathrm{5}}+\frac{\mathrm{3}}{\mathrm{1}+\mathrm{2}{log}_{\mathrm{5}} \mathrm{2}}={m} \\ $$$${let}\:{x}={log}_{\mathrm{2}} \mathrm{5}\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}+{x}}+\frac{\mathrm{3}}{\mathrm{1}+\frac{\mathrm{2}}{{x}}}={m}\Rightarrow\frac{\mathrm{1}}{\mathrm{2}+{x}}+\frac{\mathrm{3}{x}}{\mathrm{2}+{x}}={m}\Rightarrow \\ $$$$\frac{\mathrm{1}+\mathrm{3}{x}}{{x}+\mathrm{2}}={m}\Rightarrow\mathrm{1}+\mathrm{3}{x}={mx}+\mathrm{2}{m}\Rightarrow\left({m}−\mathrm{3}\right){x}=\mathrm{1}−\mathrm{2}{m}\Rightarrow \\ $$$${x}=\frac{\mathrm{1}−\mathrm{2}{m}}{{m}−\mathrm{3}} \\ $$$$ \\ $$

Answered by Rasheed.Sindhi last updated on 24/Aug/20

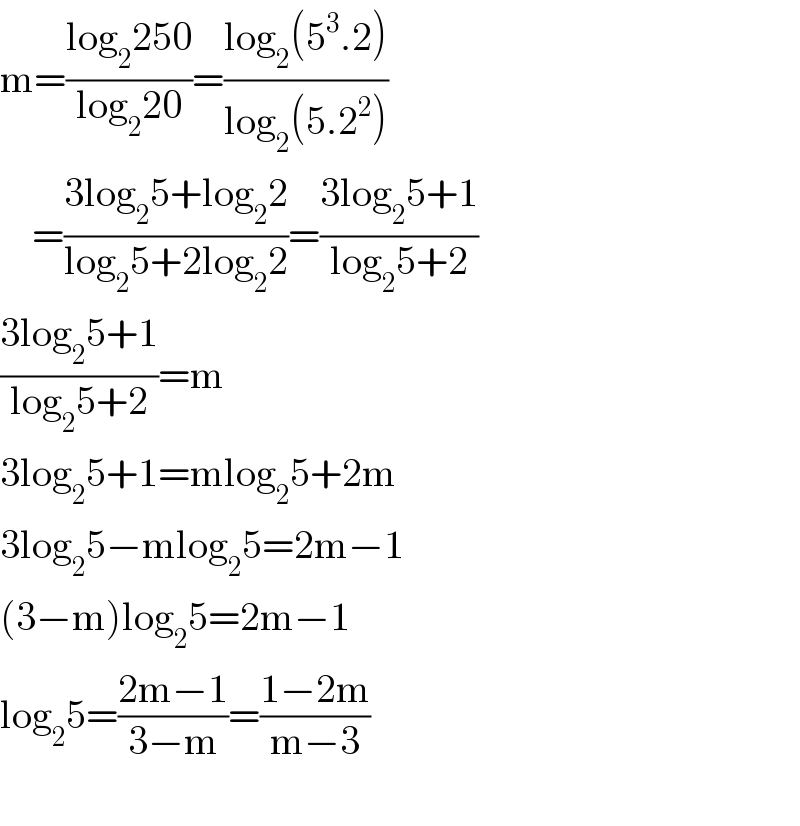
m=((log_2 250)/(log_2 20))=((log_2 (5^3 .2))/(log_2 (5.2^2 ))) =((3log_2 5+log_2 2)/(log_2 5+2log_2 2))=((3log_2 5+1)/(log_2 5+2)) ((3log_2 5+1)/(log_2 5+2))=m 3log_2 5+1=mlog_2 5+2m 3log_2 5−mlog_2 5=2m−1 (3−m)log_2 5=2m−1 log_2 5=((2m−1)/(3−m))=((1−2m)/(m−3))

$$\mathrm{m}=\frac{\mathrm{log}_{\mathrm{2}} \mathrm{250}}{\mathrm{log}_{\mathrm{2}} \mathrm{20}}=\frac{\mathrm{log}_{\mathrm{2}} \left(\mathrm{5}^{\mathrm{3}} .\mathrm{2}\right)}{\mathrm{log}_{\mathrm{2}} \left(\mathrm{5}.\mathrm{2}^{\mathrm{2}} \right)} \\ $$$$\:\:\:\:=\frac{\mathrm{3log}_{\mathrm{2}} \mathrm{5}+\mathrm{log}_{\mathrm{2}} \mathrm{2}}{\mathrm{log}_{\mathrm{2}} \mathrm{5}+\mathrm{2log}_{\mathrm{2}} \mathrm{2}}=\frac{\mathrm{3log}_{\mathrm{2}} \mathrm{5}+\mathrm{1}}{\mathrm{log}_{\mathrm{2}} \mathrm{5}+\mathrm{2}} \\ $$$$\frac{\mathrm{3log}_{\mathrm{2}} \mathrm{5}+\mathrm{1}}{\mathrm{log}_{\mathrm{2}} \mathrm{5}+\mathrm{2}}=\mathrm{m} \\ $$$$\mathrm{3log}_{\mathrm{2}} \mathrm{5}+\mathrm{1}=\mathrm{mlog}_{\mathrm{2}} \mathrm{5}+\mathrm{2m} \\ $$$$\mathrm{3log}_{\mathrm{2}} \mathrm{5}−\mathrm{mlog}_{\mathrm{2}} \mathrm{5}=\mathrm{2m}−\mathrm{1} \\ $$$$\left(\mathrm{3}−\mathrm{m}\right)\mathrm{log}_{\mathrm{2}} \mathrm{5}=\mathrm{2m}−\mathrm{1} \\ $$$$\mathrm{log}_{\mathrm{2}} \mathrm{5}=\frac{\mathrm{2m}−\mathrm{1}}{\mathrm{3}−\mathrm{m}}=\frac{\mathrm{1}−\mathrm{2m}}{\mathrm{m}−\mathrm{3}} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply