Question-109729

Question Number 109729 by lazygorilla last updated on 25/Aug/20

Answered by prakash jain last updated on 25/Aug/20

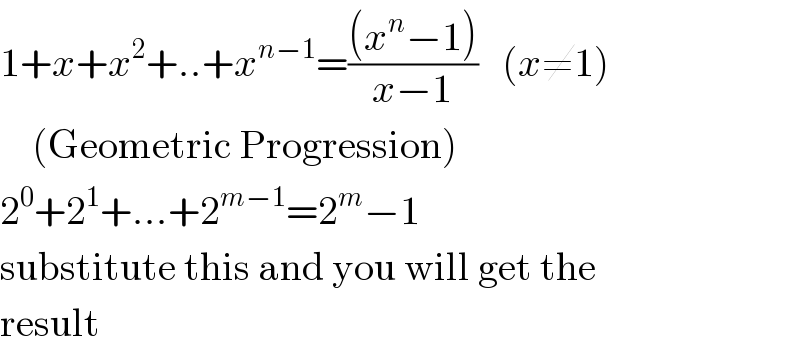
1+x+x^2 +..+x^(n−1) =(((x^n −1))/(x−1)) (x≠1) (Geometric Progression) 2^0 +2^1 +...+2^(m−1) =2^m −1 substitute this and you will get the result

$$\mathrm{1}+{x}+{x}^{\mathrm{2}} +..+{x}^{{n}−\mathrm{1}} =\frac{\left({x}^{{n}} −\mathrm{1}\right)}{{x}−\mathrm{1}}\:\:\:\left({x}\neq\mathrm{1}\right) \\ $$$$\:\:\:\:\left(\mathrm{Geometric}\:\mathrm{Progression}\right) \\ $$$$\mathrm{2}^{\mathrm{0}} +\mathrm{2}^{\mathrm{1}} +…+\mathrm{2}^{{m}−\mathrm{1}} =\mathrm{2}^{{m}} −\mathrm{1} \\ $$$$\mathrm{substitute}\:\mathrm{this}\:\mathrm{and}\:\mathrm{you}\:\mathrm{will}\:\mathrm{get}\:\mathrm{the} \\ $$$$\mathrm{result} \\ $$

Answered by bobhans last updated on 25/Aug/20

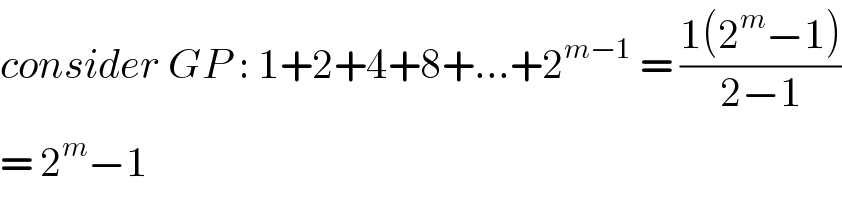
consider GP : 1+2+4+8+...+2^(m−1) = ((1(2^m −1))/(2−1)) = 2^m −1

$${consider}\:{GP}\::\:\mathrm{1}+\mathrm{2}+\mathrm{4}+\mathrm{8}+…+\mathrm{2}^{{m}−\mathrm{1}} \:=\:\frac{\mathrm{1}\left(\mathrm{2}^{{m}} −\mathrm{1}\right)}{\mathrm{2}−\mathrm{1}} \\ $$$$=\:\mathrm{2}^{{m}} −\mathrm{1}\: \\ $$

Answered by 1549442205PVT last updated on 25/Aug/20

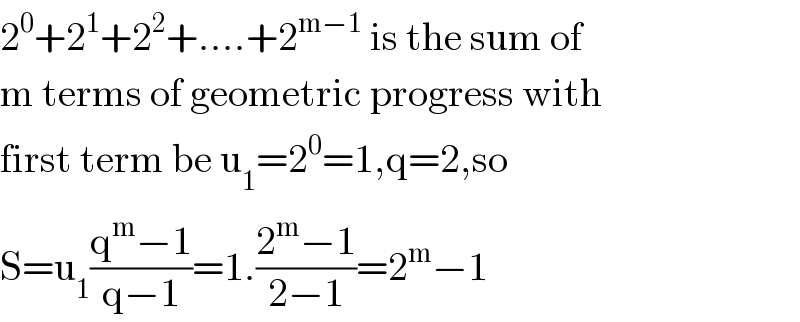
2^0 +2^1 +2^2 +....+2^(m−1) is the sum of m terms of geometric progress with first term be u_1 =2^0 =1,q=2,so S=u_1 ((q^m −1)/(q−1))=1.((2^m −1)/(2−1))=2^m −1

$$\mathrm{2}^{\mathrm{0}} +\mathrm{2}^{\mathrm{1}} +\mathrm{2}^{\mathrm{2}} +….+\mathrm{2}^{\mathrm{m}−\mathrm{1}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of} \\ $$$$\mathrm{m}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{geometric}\:\mathrm{progress}\:\mathrm{with} \\ $$$$\mathrm{first}\:\mathrm{term}\:\mathrm{be}\:\mathrm{u}_{\mathrm{1}} =\mathrm{2}^{\mathrm{0}} =\mathrm{1},\mathrm{q}=\mathrm{2},\mathrm{so} \\ $$$$\mathrm{S}=\mathrm{u}_{\mathrm{1}} \frac{\mathrm{q}^{\mathrm{m}} −\mathrm{1}}{\mathrm{q}−\mathrm{1}}=\mathrm{1}.\frac{\mathrm{2}^{\mathrm{m}} −\mathrm{1}}{\mathrm{2}−\mathrm{1}}=\mathrm{2}^{\mathrm{m}} −\mathrm{1} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply