Question Number 109834 by 675480065 last updated on 25/Aug/20

Commented by 675480065 last updated on 25/Aug/20

$$\mathrm{Greetings}. \\ $$$$\mathrm{please}\:\mathrm{i}\:\mathrm{need}\:\mathrm{help} \\ $$
Answered by mathmax by abdo last updated on 25/Aug/20

$$\left.\mathrm{1}\right)\mathrm{u}_{\mathrm{0}} =\mathrm{1}\:,\mathrm{u}_{\mathrm{1}} =\mathrm{3}\:\mathrm{and}\:\mathrm{u}_{\mathrm{n}+\mathrm{1}} =\mathrm{3u}_{\mathrm{n}} +\mathrm{4u}_{\mathrm{n}−\mathrm{1}} \:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}+\mathrm{2}} =\mathrm{3u}_{\mathrm{n}+\mathrm{1}} +\mathrm{4u}_{\mathrm{n}} \:\Rightarrow\mathrm{u}_{\mathrm{n}+\mathrm{2}} −\mathrm{3u}_{\mathrm{n}+\mathrm{1}} −\mathrm{4u}_{\mathrm{n}} =\mathrm{0}\:\rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{3x}\:−\mathrm{4}\:=\mathrm{0} \\ $$$$\Delta\:=\mathrm{9}+\mathrm{16}\:=\mathrm{25}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{3}+\mathrm{5}}{\mathrm{2}}\:=\mathrm{4}\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{5}}{\mathrm{2}}\:=−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} =\mathrm{a}\:\mathrm{4}^{\mathrm{n}} \:+\mathrm{b}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\:\mathrm{we}\:\mathrm{have}\:\mathrm{u}_{\mathrm{0}} =\mathrm{a}+\mathrm{b}\:=\mathrm{1}\:\mathrm{and}\:\mathrm{u}_{\mathrm{1}} =\mathrm{4a}−\mathrm{b}\:=\mathrm{3}\:\Rightarrow \\ $$$$\begin{cases}{\mathrm{a}+\mathrm{b}=\mathrm{1}\:\:\:\:\:\:\:_{\Rightarrow\:\:\:\:\:\:\:\:\begin{cases}{\mathrm{b}=\mathrm{1}−\mathrm{a}}\\{\mathrm{4a}−\mathrm{1}+\mathrm{a}\:=\mathrm{3}\:\Rightarrow}\end{cases}} }\\{\mathrm{4a}−\mathrm{b}\:=\mathrm{3}\:}\end{cases} \\ $$$$\begin{cases}{\mathrm{5a}\:=\mathrm{4}}\\{\mathrm{b}=\mathrm{1}−\mathrm{a}\:\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{cases}{\mathrm{a}\:=\frac{\mathrm{4}}{\mathrm{5}}\:\Rightarrow\:\:\:\:\:\begin{cases}{}\\{}\end{cases}}\\{\mathrm{b}\:=\frac{\mathrm{1}}{\mathrm{5}}}\end{cases}}\end{cases} \\ $$$$\Rightarrow\:\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{4}}{\mathrm{5}}.\mathrm{4}^{\mathrm{n}} \:+\frac{\mathrm{1}}{\mathrm{5}}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\Rightarrow\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{5}}\left\{\:\mathrm{4}^{\mathrm{n}+\mathrm{1}} \:+\left(−\mathrm{1}\right)^{\mathrm{n}} \right\} \\ $$$$\Rightarrow\:\mathrm{u}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{5}}\left\{\:\mathrm{4}^{\mathrm{3}} \:+\mathrm{1}\right\}\:=\frac{\mathrm{1}}{\mathrm{5}}\left\{\mathrm{65}\right\}\:=\frac{\mathrm{65}}{\mathrm{5}} \\ $$$$ \\ $$
Commented by 675480065 last updated on 26/Aug/20

$$\mathrm{thanks} \\ $$
Commented by abdomsup last updated on 26/Aug/20

$${you}\:{are}\:{welcome} \\ $$
Answered by Aziztisffola last updated on 25/Aug/20
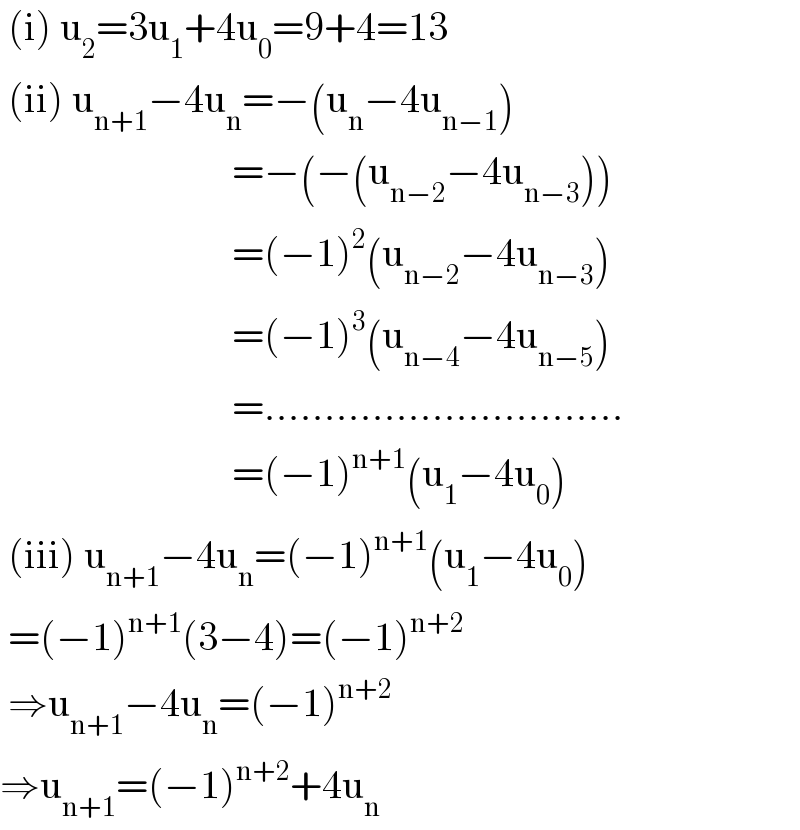
$$\:\left(\mathrm{i}\right)\:\mathrm{u}_{\mathrm{2}} =\mathrm{3u}_{\mathrm{1}} +\mathrm{4u}_{\mathrm{0}} =\mathrm{9}+\mathrm{4}=\mathrm{13} \\ $$$$\:\left(\mathrm{ii}\right)\:\mathrm{u}_{\mathrm{n}+\mathrm{1}} −\mathrm{4u}_{\mathrm{n}} =−\left(\mathrm{u}_{\mathrm{n}} −\mathrm{4u}_{\mathrm{n}−\mathrm{1}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\left(−\left(\mathrm{u}_{\mathrm{n}−\mathrm{2}} −\mathrm{4u}_{\mathrm{n}−\mathrm{3}} \right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{u}_{\mathrm{n}−\mathrm{2}} −\mathrm{4u}_{\mathrm{n}−\mathrm{3}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(−\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{u}_{\mathrm{n}−\mathrm{4}} −\mathrm{4u}_{\mathrm{n}−\mathrm{5}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=………………………… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} \left(\mathrm{u}_{\mathrm{1}} −\mathrm{4u}_{\mathrm{0}} \right) \\ $$$$\:\left(\mathrm{iii}\right)\:\mathrm{u}_{\mathrm{n}+\mathrm{1}} −\mathrm{4u}_{\mathrm{n}} =\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} \left(\mathrm{u}_{\mathrm{1}} −\mathrm{4u}_{\mathrm{0}} \right) \\ $$$$\:=\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} \left(\mathrm{3}−\mathrm{4}\right)=\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{2}} \\ $$$$\:\Rightarrow\mathrm{u}_{\mathrm{n}+\mathrm{1}} −\mathrm{4u}_{\mathrm{n}} =\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{2}} \\ $$$$\Rightarrow\mathrm{u}_{\mathrm{n}+\mathrm{1}} =\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{2}} +\mathrm{4u}_{\mathrm{n}} \\ $$
Answered by mathmax by abdo last updated on 25/Aug/20

$$\left.\mathrm{2}\right)\:\:\mathrm{i}\:\mathrm{think}\:\mathrm{tbe}\:\mathrm{relstion}\:\mathrm{is}\:\mathrm{u}_{\mathrm{n}+\mathrm{1}} −\mathrm{4u}_{\mathrm{n}} =\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{u}_{\mathrm{1}} −\mathrm{4u}_{\mathrm{0}} \right) \\ $$$$\mathrm{let}\:\mathrm{prove}\:\mathrm{it}\:\mathrm{by}\:\mathrm{recurrence}\: \\ $$$$\mathrm{n}\:=\mathrm{0}\:\Rightarrow\mathrm{u}_{\mathrm{1}} −\mathrm{4u}_{\mathrm{0}} =\left(−\mathrm{1}\right)^{\mathrm{o}} \left(\mathrm{u}_{\mathrm{1}} −\mathrm{4u}_{\mathrm{0}} \right)\:\mathrm{the}\:\mathrm{relstion}\:\mathrm{is}\:\mathrm{true}\: \\ $$$$\mathrm{let}\:\mathrm{suppose}\:\:\mathrm{u}_{\mathrm{n}+\mathrm{1}} −\mathrm{4u}_{\mathrm{n}} =\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{u}_{\mathrm{1}} −\mathrm{4u}_{\mathrm{0}} \right)\:\mathrm{and}\:\mathrm{show} \\ $$$$\mathrm{u}_{\mathrm{n}+\mathrm{2}} −\mathrm{4u}_{\mathrm{n}+\mathrm{1}} =\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} \left(\mathrm{u}_{\mathrm{1}} −\mathrm{4u}_{\mathrm{0}} \right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{u}_{\mathrm{n}+\mathrm{1}} =\mathrm{3u}_{\mathrm{n}} +\mathrm{4u}_{\mathrm{n}−\mathrm{1}} \:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}+\mathrm{2}} =\mathrm{3u}_{\mathrm{n}+\mathrm{1}} +\mathrm{4u}_{\mathrm{n}} \:\Rightarrow\mathrm{u}_{\mathrm{n}+\mathrm{2}} −\mathrm{4u}_{\mathrm{n}+\mathrm{1}} =−\mathrm{u}_{\mathrm{n}+\mathrm{1}} +\mathrm{4u}_{\mathrm{n}} \\ $$$$=−\left(\mathrm{u}_{\mathrm{n}+\mathrm{1}} −\mathrm{4u}_{\mathrm{n}} \right)\:=−\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{u}_{\mathrm{1}} −\mathrm{4u}_{\mathrm{0}} \right)\:=\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} \left(\mathrm{u}_{\mathrm{1}} −\mathrm{4u}_{\mathrm{0}} \right) \\ $$$$\mathrm{the}\:\mathrm{relation}\:\mathrm{is}\:\mathrm{true}\:\mathrm{st}\:\mathrm{term}\:\mathrm{n}+\mathrm{1} \\ $$$$ \\ $$
Commented by 675480065 last updated on 26/Aug/20
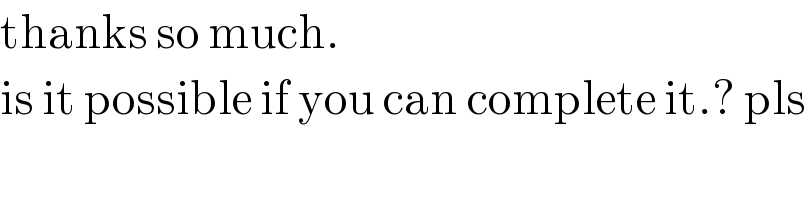
$$\mathrm{thanks}\:\mathrm{so}\:\mathrm{much}. \\ $$$$\mathrm{is}\:\mathrm{it}\:\mathrm{possible}\:\mathrm{if}\:\mathrm{you}\:\mathrm{can}\:\mathrm{complete}\:\mathrm{it}.?\:\mathrm{pls} \\ $$
