Question-109895

Question Number 109895 by qwerty111 last updated on 26/Aug/20

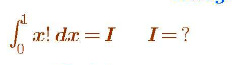
Commented by mathdave last updated on 26/Aug/20

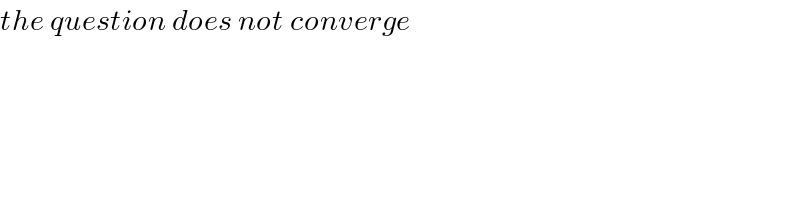
$${the}\:{question}\:{does}\:{not}\:{converge} \\ $$

Commented by Her_Majesty last updated on 26/Aug/20

sorry but Γ(x) is continuous, it had been the main reason for its “birth”. it is not defined only for x∈Z^−

$${sorry}\:{but}\:\Gamma\left({x}\right)\:{is}\:{continuous},\:{it}\:{had}\:{been}\:{the} \\ $$$${main}\:{reason}\:{for}\:{its}\:“{birth}''.\:{it}\:{is}\:{not}\:{defined} \\ $$$${only}\:{for}\:{x}\in\mathbb{Z}^{−} \\ $$

Commented by Her_Majesty last updated on 26/Aug/20

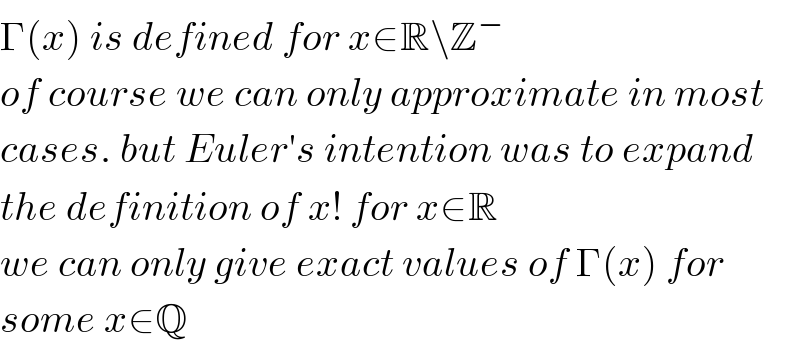
Γ(x) is defined for x∈R\Z^− of course we can only approximate in most cases. but Euler′s intention was to expand the definition of x! for x∈R we can only give exact values of Γ(x) for some x∈Q

$$\Gamma\left({x}\right)\:{is}\:{defined}\:{for}\:{x}\in\mathbb{R}\backslash\mathbb{Z}^{−} \\ $$$${of}\:{course}\:{we}\:{can}\:{only}\:{approximate}\:{in}\:{most} \\ $$$${cases}.\:{but}\:{Euler}'{s}\:{intention}\:{was}\:{to}\:{expand} \\ $$$${the}\:{definition}\:{of}\:{x}!\:{for}\:{x}\in\mathbb{R} \\ $$$${we}\:{can}\:{only}\:{give}\:{exact}\:{values}\:{of}\:\Gamma\left({x}\right)\:{for} \\ $$$${some}\:{x}\in\mathbb{Q} \\ $$

Answered by Her_Majesty last updated on 26/Aug/20

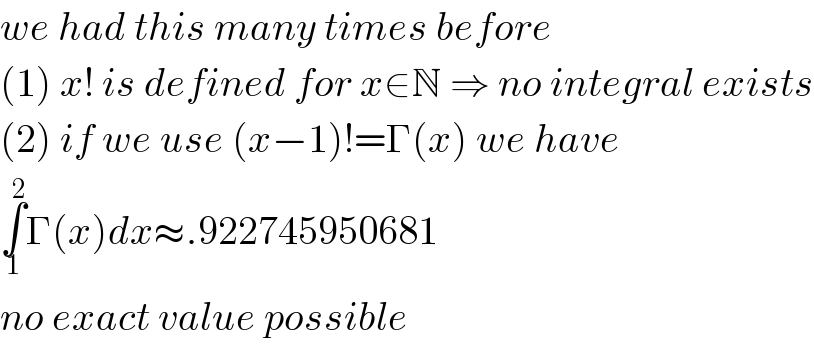
we had this many times before (1) x! is defined for x∈N ⇒ no integral exists (2) if we use (x−1)!=Γ(x) we have ∫_1 ^2 Γ(x)dx≈.922745950681 no exact value possible

$${we}\:{had}\:{this}\:{many}\:{times}\:{before} \\ $$$$\left(\mathrm{1}\right)\:{x}!\:{is}\:{defined}\:{for}\:{x}\in\mathbb{N}\:\Rightarrow\:{no}\:{integral}\:{exists} \\ $$$$\left(\mathrm{2}\right)\:{if}\:{we}\:{use}\:\left({x}−\mathrm{1}\right)!=\Gamma\left({x}\right)\:{we}\:{have} \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\Gamma\left({x}\right){dx}\approx.\mathrm{922745950681} \\ $$$${no}\:{exact}\:{value}\:{possible} \\ $$

Commented by 1549442205PVT last updated on 27/Aug/20

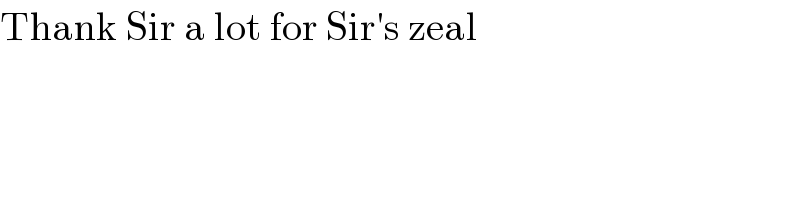
$$\mathrm{Thank}\:\mathrm{Sir}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{for}\:\mathrm{Sir}'\mathrm{s}\:\mathrm{zeal} \\ $$

Commented by 1549442205PVT last updated on 26/Aug/20

Thank Sir a lot.But i don′t know how to calculate Γ(1/(√2)),Γ(1/(√5)).If don′t calculate that values then means it isn′t defined on set of irrational numbers which if such as it is is interrupted anywhere,so can′t have its defined integration because on segment[0,1] it has an infinite number of interrupted points

$$\mathrm{Thank}\:\mathrm{Sir}\:\mathrm{a}\:\mathrm{lot}.\mathrm{But}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{know} \\ $$$$\mathrm{how}\:\mathrm{to}\:\mathrm{calculate}\:\Gamma\left(\mathrm{1}/\sqrt{\mathrm{2}}\right),\Gamma\left(\mathrm{1}/\sqrt{\mathrm{5}}\right).\mathrm{If} \\ $$$$\mathrm{don}'\mathrm{t}\:\mathrm{calculate}\:\mathrm{that}\:\mathrm{values}\:\mathrm{then} \\ $$$$\mathrm{means}\:\mathrm{it}\:\mathrm{isn}'\mathrm{t}\:\mathrm{defined}\:\mathrm{on}\:\mathrm{set}\:\mathrm{of} \\ $$$$\mathrm{irrational}\:\mathrm{numbers}\:\mathrm{which}\:\mathrm{if}\:\mathrm{such}\:\mathrm{as} \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{is}\:\mathrm{interrupted}\:\mathrm{anywhere},\mathrm{so}\: \\ $$$$\mathrm{can}'\mathrm{t}\:\mathrm{have}\:\mathrm{its}\:\mathrm{defined}\:\mathrm{integration} \\ $$$$\mathrm{because}\:\mathrm{on}\:\mathrm{segment}\left[\mathrm{0},\mathrm{1}\right]\:\mathrm{it}\:\mathrm{has}\:\mathrm{an}\: \\ $$$$\mathrm{infinite}\:\mathrm{number}\:\mathrm{of}\:\mathrm{interrupted}\:\mathrm{points} \\ $$

Commented by Her_Majesty last updated on 26/Aug/20

you are wrong; read this https://en.wikipedia.org/wiki/Gamma_function

Commented by Her_Majesty last updated on 26/Aug/20

Γ(1/(√2))≈1.28694088 Γ(1/(√5))≈1.98046902

$$\Gamma\left(\mathrm{1}/\sqrt{\mathrm{2}}\right)\approx\mathrm{1}.\mathrm{28694088} \\ $$$$\Gamma\left(\mathrm{1}/\sqrt{\mathrm{5}}\right)\approx\mathrm{1}.\mathrm{98046902} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply