Question-109905

Question Number 109905 by ajfour last updated on 26/Aug/20

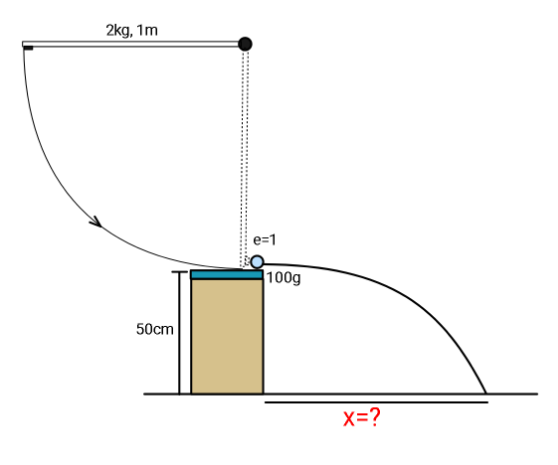
Answered by mr W last updated on 26/Aug/20

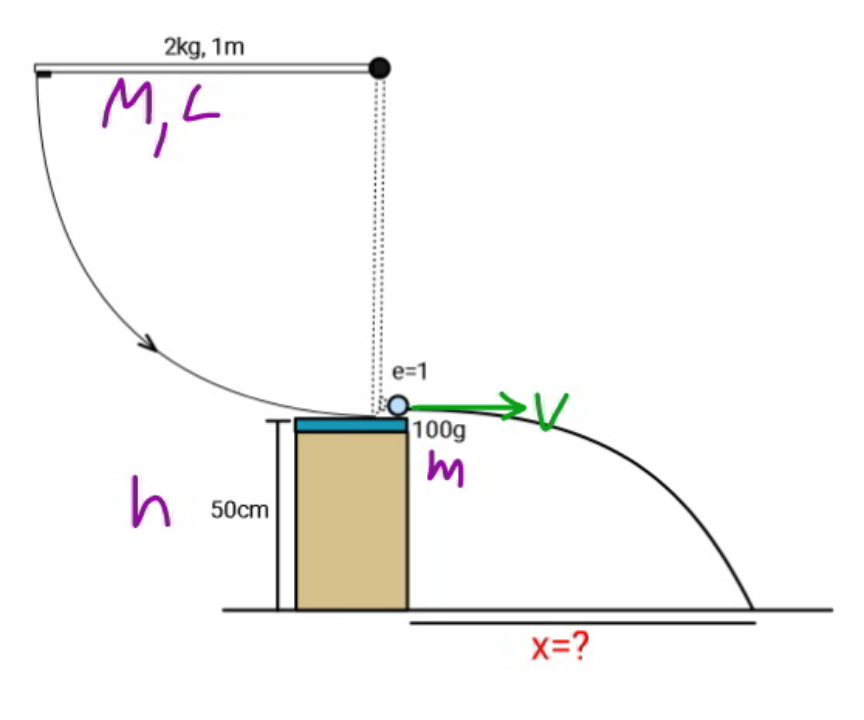
Commented by mr W last updated on 26/Aug/20

Mg×(L/2)=(1/2)Iω^2 =(1/2)×((ML^2 )/3)ω_i ^2 ω_i =(√((3g)/L)) eω_i L=v−ω_f L ⇒ω_f =(v/L)−ω_i =(v/L)−(√((3g)/L)) ((ML^2 )/3)ω_i =((ML^2 )/3)ω_f +mvL ω_i =ω_f +mv×(3/(ML)) (√((3g)/L))=(v/L)−(√((3g)/L))+mv×(3/(ML)) ⇒v=((2(√(3gL)))/(1+((3m)/M))) x=vt=v(√((2h)/g))=((2(√(6Lh)))/(1+((3m)/M))) x=((2(√(6×1×0.5)))/(1+((3×0.1)/2)))=((40(√3))/(23))=3.01 m

$${Mg}×\frac{{L}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}{I}\omega^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{{ML}^{\mathrm{2}} }{\mathrm{3}}\omega_{{i}} ^{\mathrm{2}} \\ $$$$\omega_{{i}} =\sqrt{\frac{\mathrm{3}{g}}{{L}}} \\ $$$${e}\omega_{{i}} {L}={v}−\omega_{{f}} {L} \\ $$$$\Rightarrow\omega_{{f}} =\frac{{v}}{{L}}−\omega_{{i}} =\frac{{v}}{{L}}−\sqrt{\frac{\mathrm{3}{g}}{{L}}} \\ $$$$\frac{{ML}^{\mathrm{2}} }{\mathrm{3}}\omega_{{i}} =\frac{{ML}^{\mathrm{2}} }{\mathrm{3}}\omega_{{f}} +{mvL} \\ $$$$\omega_{{i}} =\omega_{{f}} +{mv}×\frac{\mathrm{3}}{{ML}} \\ $$$$\sqrt{\frac{\mathrm{3}{g}}{{L}}}=\frac{{v}}{{L}}−\sqrt{\frac{\mathrm{3}{g}}{{L}}}+{mv}×\frac{\mathrm{3}}{{ML}} \\ $$$$\Rightarrow{v}=\frac{\mathrm{2}\sqrt{\mathrm{3}{gL}}}{\mathrm{1}+\frac{\mathrm{3}{m}}{{M}}} \\ $$$${x}={vt}={v}\sqrt{\frac{\mathrm{2}{h}}{{g}}}=\frac{\mathrm{2}\sqrt{\mathrm{6}{Lh}}}{\mathrm{1}+\frac{\mathrm{3}{m}}{{M}}} \\ $$$${x}=\frac{\mathrm{2}\sqrt{\mathrm{6}×\mathrm{1}×\mathrm{0}.\mathrm{5}}}{\mathrm{1}+\frac{\mathrm{3}×\mathrm{0}.\mathrm{1}}{\mathrm{2}}}=\frac{\mathrm{40}\sqrt{\mathrm{3}}}{\mathrm{23}}=\mathrm{3}.\mathrm{01}\:{m} \\ $$

Commented by ajfour last updated on 27/Aug/20

$${Thank}\:{you}\:{Sir},\:{very}\:{nice}\:{solution}. \\ $$

Facebook Tweet Pin

Question-109905

Leave a Reply Cancel reply