Question Number 109948 by mnjuly1970 last updated on 26/Aug/20
Answered by 1549442205PVT last updated on 26/Aug/20

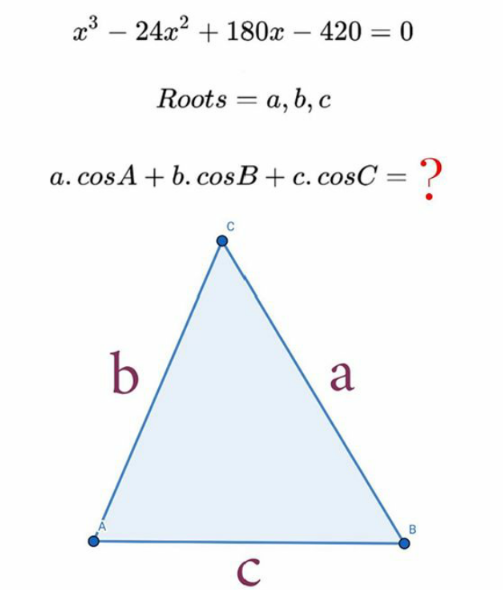
$$\mathrm{acosA}=\mathrm{a}.\frac{\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }{\mathrm{2bc}}=\frac{\mathrm{a}^{\mathrm{2}} \left(\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)}{\mathrm{2abc}}. \\ $$$$\mathrm{Similarly},\mathrm{we}\:\mathrm{have}\:\mathrm{the}\:\mathrm{other}\:\mathrm{equalities} \\ $$$$\mathrm{for}\:\mathrm{b},\mathrm{c}\:\mathrm{Hence} \\ $$$$\mathrm{acosA}+\mathrm{bcosB}+\mathrm{c}.\mathrm{cosC}=\underset{\mathrm{cyc}} {\Sigma}\frac{\mathrm{a}^{\mathrm{2}} \left(\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)}{\mathrm{2abc}} \\ $$$$=\:\frac{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \mathrm{a}^{\mathrm{2}} −\mathrm{0}.\mathrm{5}\left(\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} +\mathrm{c}^{\mathrm{4}} \right)}{\mathrm{abc}}\:\:\:\left(\ast\right) \\ $$$$\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{are}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{x}^{\mathrm{3}} −\mathrm{24x}^{\mathrm{2}} +\mathrm{180x}−\mathrm{420}\:\mathrm{by}\:\mathrm{Viete}'\mathrm{s}\:\mathrm{theorem} \\ $$$$\mathrm{we}\:\mathrm{have\begin{cases}{\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{24}}\\{\mathrm{ab}+\mathrm{bc}+\mathrm{ca}=\mathrm{180}}\\{\mathrm{abc}=\mathrm{420}}\end{cases}} \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} =\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{ab}+\mathrm{bc}+\mathrm{ca}\right) \\ $$$$=\mathrm{24}^{\mathrm{2}} −\mathrm{2}.\mathrm{180}=\mathrm{576}−\mathrm{360}=\mathrm{216}\:\:\: \\ $$$$\left(\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \mathrm{a}^{\mathrm{2}} \right)=\left(\mathrm{ab}+\mathrm{bc}+\mathrm{ca}\right)^{\mathrm{2}} −\mathrm{2abc}\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right) \\ $$$$=\mathrm{180}^{\mathrm{2}} −\mathrm{2}.\mathrm{420}.\mathrm{24}=\mathrm{32400}−\mathrm{20160}=\mathrm{12240}\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} +\mathrm{c}^{\mathrm{4}} \right)=\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \mathrm{a}^{\mathrm{2}} \right) \\ $$$$=\mathrm{216}^{\mathrm{2}} −\mathrm{2}.\mathrm{12240}=\mathrm{22176}\left(\mathrm{2}\right) \\ $$$$\mathrm{Replace}\:\left(\mathrm{1}\right)\left(\mathrm{2}\right)\mathrm{and}\:\mathrm{abc}\:=\mathrm{420}\:\:\mathrm{into}\:\left(\ast\right)\: \\ $$$$\mathrm{we}\:\mathrm{get}\:\frac{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \mathrm{a}^{\mathrm{2}} −\left(\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} +\mathrm{c}^{\mathrm{4}} \right)}{\mathrm{abc}}\:\: \\ $$$$=\frac{\mathrm{12240}−\mathrm{0}.\mathrm{5}×\mathrm{22176}}{\mathrm{420}}=\frac{\mathrm{96}}{\mathrm{35}} \\ $$$$\mathrm{Thus},\mathrm{acosA}+\mathrm{bcosB}+\mathrm{c}.\mathrm{cosC}=\frac{\mathrm{96}}{\mathrm{35}} \\ $$
Commented by mnjuly1970 last updated on 27/Aug/20
$${excellent}…{thank}\:{you}\:\:{sir}.. \\ $$
