Question Number 110049 by mathdave last updated on 26/Aug/20
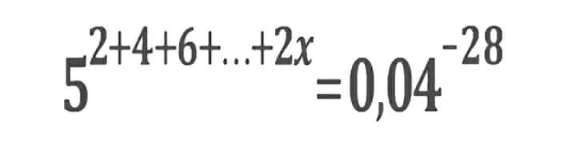
Answered by floor(10²Eta[1]) last updated on 27/Aug/20
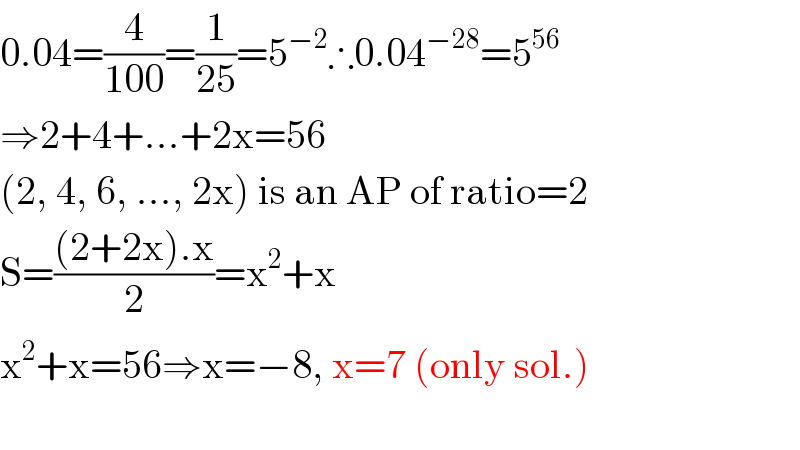
$$\mathrm{0}.\mathrm{04}=\frac{\mathrm{4}}{\mathrm{100}}=\frac{\mathrm{1}}{\mathrm{25}}=\mathrm{5}^{−\mathrm{2}} \therefore\mathrm{0}.\mathrm{04}^{−\mathrm{28}} =\mathrm{5}^{\mathrm{56}} \\ $$$$\Rightarrow\mathrm{2}+\mathrm{4}+…+\mathrm{2x}=\mathrm{56} \\ $$$$\left(\mathrm{2},\:\mathrm{4},\:\mathrm{6},\:…,\:\mathrm{2x}\right)\:\mathrm{is}\:\mathrm{an}\:\mathrm{AP}\:\mathrm{of}\:\mathrm{ratio}=\mathrm{2} \\ $$$$\mathrm{S}=\frac{\left(\mathrm{2}+\mathrm{2x}\right).\mathrm{x}}{\mathrm{2}}=\mathrm{x}^{\mathrm{2}} +\mathrm{x} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{x}=\mathrm{56}\Rightarrow\mathrm{x}=−\mathrm{8},\:\mathrm{x}=\mathrm{7}\:\left(\mathrm{only}\:\mathrm{sol}.\right) \\ $$$$ \\ $$
Answered by john santu last updated on 26/Aug/20
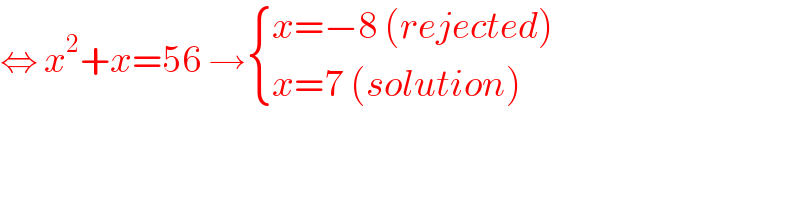
$$\Leftrightarrow\:{x}^{\mathrm{2}} +{x}=\mathrm{56}\:\rightarrow\begin{cases}{{x}=−\mathrm{8}\:\left({rejected}\right)}\\{{x}=\mathrm{7}\:\left({solution}\right)}\end{cases} \\ $$
Commented by john santu last updated on 27/Aug/20
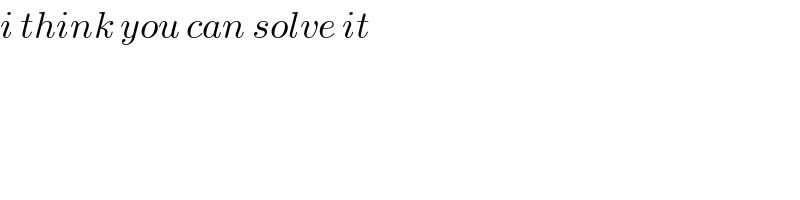
$${i}\:{think}\:{you}\:{can}\:{solve}\:{it}\: \\ $$
Commented by mathdave last updated on 27/Aug/20
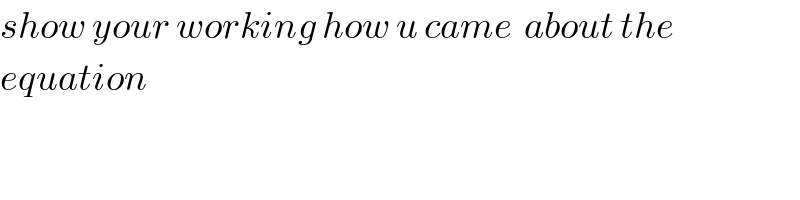
$${show}\:{your}\:{working}\:{how}\:{u}\:{came}\:\:{about}\:{the}\: \\ $$$${equation}\: \\ $$
Commented by mathdave last updated on 27/Aug/20
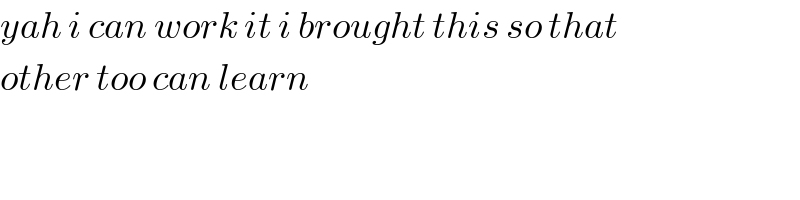
$${yah}\:{i}\:{can}\:{work}\:{it}\:{i}\:{brought}\:{this}\:{so}\:{that} \\ $$$${other}\:{too}\:{can}\:{learn} \\ $$
Answered by 1549442205PVT last updated on 27/Aug/20
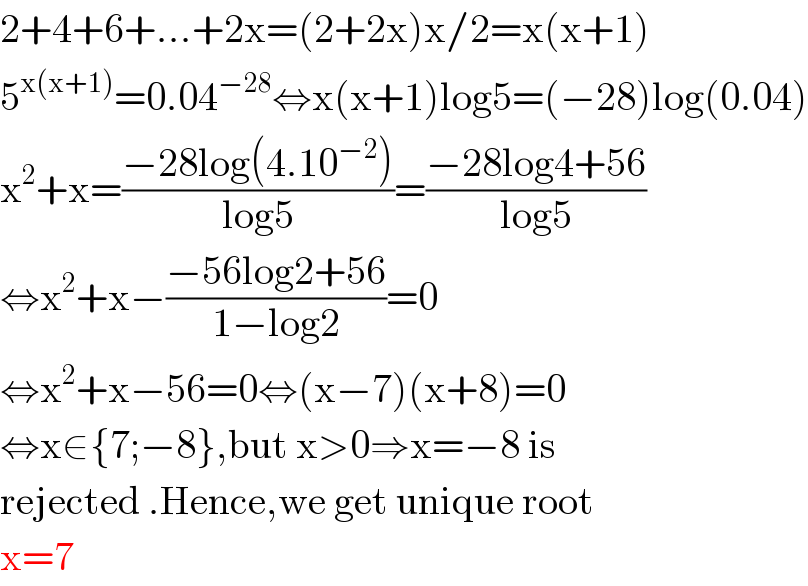
$$\mathrm{2}+\mathrm{4}+\mathrm{6}+…+\mathrm{2x}=\left(\mathrm{2}+\mathrm{2x}\right)\mathrm{x}/\mathrm{2}=\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right) \\ $$$$\mathrm{5}^{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)} =\mathrm{0}.\mathrm{04}^{−\mathrm{28}} \Leftrightarrow\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\mathrm{log5}=\left(−\mathrm{28}\right)\mathrm{log}\left(\mathrm{0}.\mathrm{04}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{x}=\frac{−\mathrm{28log}\left(\mathrm{4}.\mathrm{10}^{−\mathrm{2}} \right)}{\mathrm{log5}}=\frac{−\mathrm{28log4}+\mathrm{56}}{\mathrm{log5}} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\frac{−\mathrm{56log2}+\mathrm{56}}{\mathrm{1}−\mathrm{log2}}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{56}=\mathrm{0}\Leftrightarrow\left(\mathrm{x}−\mathrm{7}\right)\left(\mathrm{x}+\mathrm{8}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}\in\left\{\mathrm{7};−\mathrm{8}\right\},\mathrm{but}\:\mathrm{x}>\mathrm{0}\Rightarrow\mathrm{x}=−\mathrm{8}\:\mathrm{is} \\ $$$$\mathrm{rejected}\:.\mathrm{Hence},\mathrm{we}\:\mathrm{get}\:\mathrm{unique}\:\mathrm{root} \\ $$$$\mathrm{x}=\mathrm{7} \\ $$
Answered by Rasheed.Sindhi last updated on 27/Aug/20
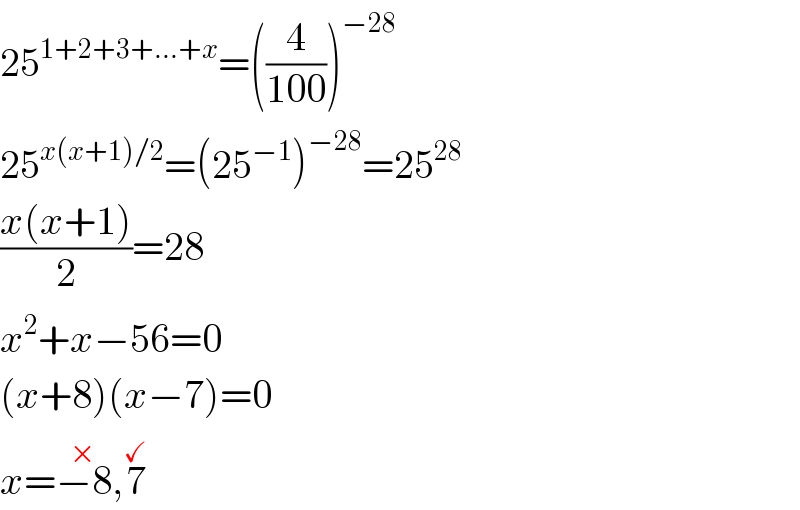
$$\mathrm{25}^{\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{x}} =\left(\frac{\mathrm{4}}{\mathrm{100}}\right)^{−\mathrm{28}} \\ $$$$\mathrm{25}^{{x}\left({x}+\mathrm{1}\right)/\mathrm{2}} =\left(\mathrm{25}^{−\mathrm{1}} \right)^{−\mathrm{28}} =\mathrm{25}^{\mathrm{28}} \\ $$$$\frac{{x}\left({x}+\mathrm{1}\right)}{\mathrm{2}}=\mathrm{28} \\ $$$${x}^{\mathrm{2}} +{x}−\mathrm{56}=\mathrm{0} \\ $$$$\left({x}+\mathrm{8}\right)\left({x}−\mathrm{7}\right)=\mathrm{0} \\ $$$${x}=\overset{×} {−\mathrm{8}},\overset{\checkmark} {\mathrm{7}} \\ $$
