Menu Close

Question-110092

Tinku Tara 0 Comments
Pin




Question Number 110092 by bemath last updated on 27/Aug/20
Answered by 1549442205PVT last updated on 27/Aug/20
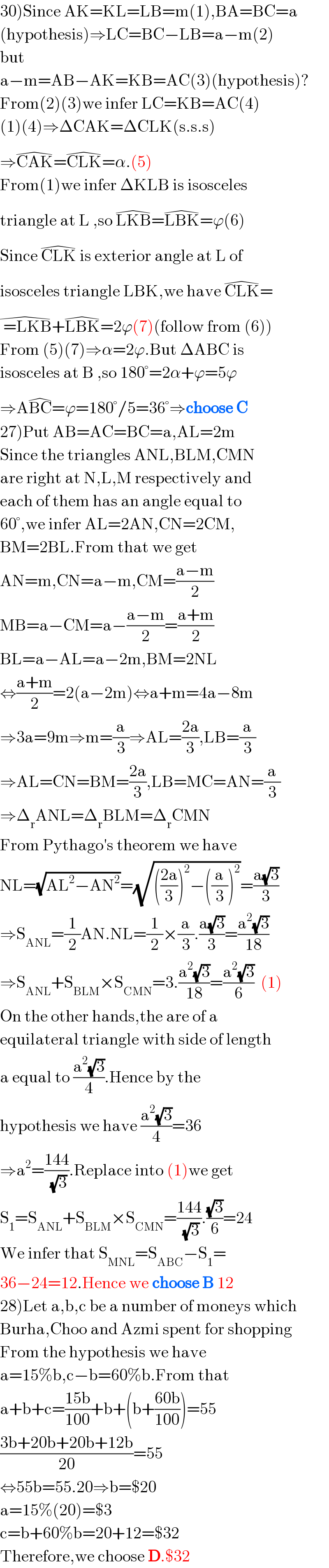
30)Since AK=KL=LB=m(1),BA=BC=a (hypothesis)⇒LC=BC−LB=a−m(2) but a−m=AB−AK=KB=AC(3)(hypothesis)? From(2)(3)we infer LC=KB=AC(4) (1)(4)⇒ΔCAK=ΔCLK(s.s.s) ⇒CAK^(�) =CLK^(�) =α.(5) From(1)we infer ΔKLB is isosceles triangle at L ,so LKB^(�) =LBK^(�) =ϕ(6) Since CLK^(�) is exterior angle at L of isosceles triangle LBK,we have CLK^(�) = =LKB^(�) +LBK^(�) =2ϕ(7)(follow from (6)) From (5)(7)⇒α=2ϕ.But ΔABC is isosceles at B ,so 180°=2α+ϕ=5ϕ ⇒ABC^(�) =ϕ=180°/5=36°⇒choose C 27)Put AB=AC=BC=a,AL=2m Since the triangles ANL,BLM,CMN are right at N,L,M respectively and each of them has an angle equal to 60°,we infer AL=2AN,CN=2CM, BM=2BL.From that we get AN=m,CN=a−m,CM=((a−m)/2) MB=a−CM=a−((a−m)/2)=((a+m)/2) BL=a−AL=a−2m,BM=2NL ⇔((a+m)/2)=2(a−2m)⇔a+m=4a−8m ⇒3a=9m⇒m=(a/3)⇒AL=((2a)/3),LB=(a/3) ⇒AL=CN=BM=((2a)/3),LB=MC=AN=(a/3) ⇒Δ_r ANL=Δ_r BLM=Δ_r CMN From Pythago′s theorem we have NL=(√(AL^2 −AN^2 ))=(√((((2a)/3))^2 −((a/3))^2 ))=((a(√3))/3) ⇒S_(ANL) =(1/2)AN.NL=(1/2)×(a/3).((a(√3))/3)=((a^2 (√3))/(18)) ⇒S_(ANL) +S_(BLM) ×S_(CMN) =3.((a^2 (√3))/(18))=((a^2 (√3))/6) (1) On the other hands,the are of a equilateral triangle with side of length a equal to ((a^2 (√3))/4).Hence by the hypothesis we have ((a^2 (√3))/4)=36 ⇒a^2 =((144)/( (√3))).Replace into (1)we get S_1 =S_(ANL) +S_(BLM) ×S_(CMN) =((144)/( (√3))).((√3)/6)=24 We infer that S_(MNL) =S_(ABC) −S_1 = 36−24=12.Hence we choose B 12 28)Let a,b,c be a number of moneys which Burha,Choo and Azmi spent for shopping From the hypothesis we have a=15%b,c−b=60%b.From that a+b+c=((15b)/(100))+b+(b+((60b)/(100)))=55 ((3b+20b+20b+12b)/(20))=55 ⇔55b=55.20⇒b=$20 a=15%(20)=$3 c=b+60%b=20+12=$32 Therefore,we choose D.$32
$$\left.\mathrm{30}\right)\mathrm{Since}\:\mathrm{AK}=\mathrm{KL}=\mathrm{LB}=\mathrm{m}\left(\mathrm{1}\right),\mathrm{BA}=\mathrm{BC}=\mathrm{a} \\ $$$$\left(\mathrm{hypothesis}\right)\Rightarrow\mathrm{LC}=\mathrm{BC}−\mathrm{LB}=\mathrm{a}−\mathrm{m}\left(\mathrm{2}\right) \\ $$$$\mathrm{but} \\ $$$$\mathrm{a}−\mathrm{m}=\mathrm{AB}−\mathrm{AK}=\mathrm{KB}=\mathrm{AC}\left(\mathrm{3}\right)\left(\mathrm{hypothesis}\right)? \\ $$$$\mathrm{From}\left(\mathrm{2}\right)\left(\mathrm{3}\right)\mathrm{we}\:\mathrm{infer}\:\mathrm{LC}=\mathrm{KB}=\mathrm{AC}\left(\mathrm{4}\right) \\ $$$$\left(\mathrm{1}\right)\left(\mathrm{4}\right)\Rightarrow\Delta\mathrm{CAK}=\Delta\mathrm{CLK}\left(\mathrm{s}.\mathrm{s}.\mathrm{s}\right) \\ $$$$\Rightarrow\widehat {\mathrm{CAK}}=\widehat {\mathrm{CLK}}=\alpha.\left(\mathrm{5}\right) \\ $$$$\mathrm{From}\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{infer}\:\Delta\mathrm{KLB}\:\mathrm{is}\:\mathrm{isosceles} \\ $$$$\mathrm{triangle}\:\mathrm{at}\:\mathrm{L}\:,\mathrm{so}\:\widehat {\mathrm{LKB}}=\widehat {\mathrm{LBK}}=\varphi\left(\mathrm{6}\right) \\ $$$$\mathrm{Since}\:\widehat {\mathrm{CLK}}\:\mathrm{is}\:\mathrm{exterior}\:\mathrm{angle}\:\mathrm{at}\:\mathrm{L}\:\mathrm{of} \\ $$$$\mathrm{isosceles}\:\mathrm{triangle}\:\mathrm{LBK},\mathrm{we}\:\mathrm{have}\:\widehat {\mathrm{CLK}}=\: \\ $$$$\widehat {\:=\mathrm{LKB}}+\widehat {\mathrm{LBK}}=\mathrm{2}\varphi\left(\mathrm{7}\right)\left(\mathrm{follow}\:\mathrm{from}\:\left(\mathrm{6}\right)\right) \\ $$$$\mathrm{From}\:\left(\mathrm{5}\right)\left(\mathrm{7}\right)\Rightarrow\alpha=\mathrm{2}\varphi.\mathrm{But}\:\Delta\mathrm{ABC}\:\mathrm{is} \\ $$$$\mathrm{isosceles}\:\mathrm{at}\:\mathrm{B}\:,\mathrm{so}\:\mathrm{180}°=\mathrm{2}\alpha+\varphi=\mathrm{5}\varphi \\ $$$$\Rightarrow\mathrm{A}\widehat {\mathrm{BC}}=\varphi=\mathrm{180}°/\mathrm{5}=\mathrm{36}°\Rightarrow\boldsymbol{\mathrm{choose}}\:\boldsymbol{\mathrm{C}} \\ $$$$\left.\mathrm{27}\right)\mathrm{Put}\:\mathrm{AB}=\mathrm{AC}=\mathrm{BC}=\mathrm{a},\mathrm{AL}=\mathrm{2m} \\ $$$$\mathrm{Since}\:\mathrm{the}\:\mathrm{triangles}\:\mathrm{ANL},\mathrm{BLM},\mathrm{CMN} \\ $$$$\mathrm{are}\:\mathrm{right}\:\mathrm{at}\:\mathrm{N},\mathrm{L},\mathrm{M}\:\mathrm{respectively}\:\mathrm{and} \\ $$$$\mathrm{each}\:\mathrm{of}\:\mathrm{them}\:\mathrm{has}\:\mathrm{an}\:\mathrm{angle}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\mathrm{60}°,\mathrm{we}\:\mathrm{infer}\:\mathrm{AL}=\mathrm{2AN},\mathrm{CN}=\mathrm{2CM}, \\ $$$$\mathrm{BM}=\mathrm{2BL}.\mathrm{From}\:\mathrm{that}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{AN}=\mathrm{m},\mathrm{CN}=\mathrm{a}−\mathrm{m},\mathrm{CM}=\frac{\mathrm{a}−\mathrm{m}}{\mathrm{2}} \\ $$$$\mathrm{MB}=\mathrm{a}−\mathrm{CM}=\mathrm{a}−\frac{\mathrm{a}−\mathrm{m}}{\mathrm{2}}=\frac{\mathrm{a}+\mathrm{m}}{\mathrm{2}}\:\:\: \\ $$$$\mathrm{BL}=\mathrm{a}−\mathrm{AL}=\mathrm{a}−\mathrm{2m},\mathrm{BM}=\mathrm{2NL} \\ $$$$\Leftrightarrow\frac{\mathrm{a}+\mathrm{m}}{\mathrm{2}}=\mathrm{2}\left(\mathrm{a}−\mathrm{2m}\right)\Leftrightarrow\mathrm{a}+\mathrm{m}=\mathrm{4a}−\mathrm{8m} \\ $$$$\Rightarrow\mathrm{3a}=\mathrm{9m}\Rightarrow\mathrm{m}=\frac{\mathrm{a}}{\mathrm{3}}\Rightarrow\mathrm{AL}=\frac{\mathrm{2a}}{\mathrm{3}},\mathrm{LB}=\frac{\mathrm{a}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{AL}=\mathrm{CN}=\mathrm{BM}=\frac{\mathrm{2a}}{\mathrm{3}},\mathrm{LB}=\mathrm{MC}=\mathrm{AN}=\frac{\mathrm{a}}{\mathrm{3}} \\ $$$$\Rightarrow\Delta_{\mathrm{r}} \mathrm{ANL}=\Delta_{\mathrm{r}} \mathrm{BLM}=\Delta_{\mathrm{r}} \mathrm{CMN} \\ $$$$\mathrm{From}\:\mathrm{Pythago}'\mathrm{s}\:\mathrm{theorem}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{NL}=\sqrt{\mathrm{AL}^{\mathrm{2}} −\mathrm{AN}^{\mathrm{2}} }=\sqrt{\left(\frac{\mathrm{2a}}{\mathrm{3}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{a}}{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\mathrm{a}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{S}_{\mathrm{ANL}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{AN}.\mathrm{NL}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{a}}{\mathrm{3}}.\frac{\mathrm{a}\sqrt{\mathrm{3}}}{\mathrm{3}}=\frac{\mathrm{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{18}} \\ $$$$\Rightarrow\mathrm{S}_{\mathrm{ANL}} +\mathrm{S}_{\mathrm{BLM}} ×\mathrm{S}_{\mathrm{CMN}} =\mathrm{3}.\frac{\mathrm{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{18}}=\frac{\mathrm{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{6}}\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{On}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hands},\mathrm{the}\:\mathrm{are}\:\mathrm{of}\:\mathrm{a} \\ $$$$\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{with}\:\mathrm{side}\:\mathrm{of}\:\mathrm{length} \\ $$$$\mathrm{a}\:\mathrm{equal}\:\mathrm{to}\:\frac{\mathrm{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}.\mathrm{Hence}\:\mathrm{by}\:\mathrm{the} \\ $$$$\mathrm{hypothesis}\:\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}=\mathrm{36} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} =\frac{\mathrm{144}}{\:\sqrt{\mathrm{3}}}.\mathrm{Replace}\:\mathrm{into}\:\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{S}_{\mathrm{1}} =\mathrm{S}_{\mathrm{ANL}} +\mathrm{S}_{\mathrm{BLM}} ×\mathrm{S}_{\mathrm{CMN}} =\frac{\mathrm{144}}{\:\sqrt{\mathrm{3}}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}=\mathrm{24} \\ $$$$\mathrm{We}\:\mathrm{infer}\:\mathrm{that}\:\mathrm{S}_{\mathrm{MNL}} =\mathrm{S}_{\mathrm{ABC}} −\mathrm{S}_{\mathrm{1}} = \\ $$$$\mathrm{36}−\mathrm{24}=\mathrm{12}.\mathrm{Hence}\:\mathrm{we}\:\boldsymbol{\mathrm{choose}}\:\boldsymbol{\mathrm{B}}\:\mathrm{12} \\ $$$$\left.\mathrm{28}\right)\mathrm{Let}\:\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{be}\:\mathrm{a}\:\mathrm{number}\:\mathrm{of}\:\mathrm{moneys}\:\mathrm{which} \\ $$$$\mathrm{Burha},\mathrm{Choo}\:\mathrm{and}\:\mathrm{Azmi}\:\mathrm{spent}\:\mathrm{for}\:\mathrm{shopping} \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{a}=\mathrm{15\%b},\mathrm{c}−\mathrm{b}=\mathrm{60\%b}.\mathrm{From}\:\mathrm{that} \\ $$$$\mathrm{a}+\mathrm{b}+\mathrm{c}=\frac{\mathrm{15b}}{\mathrm{100}}+\mathrm{b}+\left(\mathrm{b}+\frac{\mathrm{60b}}{\mathrm{100}}\right)=\mathrm{55} \\ $$$$\frac{\mathrm{3b}+\mathrm{20b}+\mathrm{20b}+\mathrm{12b}}{\mathrm{20}}=\mathrm{55} \\ $$$$\Leftrightarrow\mathrm{55b}=\mathrm{55}.\mathrm{20}\Rightarrow\mathrm{b}=\$\mathrm{20} \\ $$$$\mathrm{a}=\mathrm{15\%}\left(\mathrm{20}\right)=\$\mathrm{3} \\ $$$$\mathrm{c}=\mathrm{b}+\mathrm{60\%b}=\mathrm{20}+\mathrm{12}=\$\mathrm{32} \\ $$$$\mathrm{Therefore},\mathrm{we}\:\mathrm{choose}\:\boldsymbol{\mathrm{D}}.\$\mathrm{32}\: \\ $$
Commented by bemath last updated on 27/Aug/20

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *