Menu Close

Question-110143

Tinku Tara 0 Comments
Pin




Question Number 110143 by I want to learn more last updated on 27/Aug/20
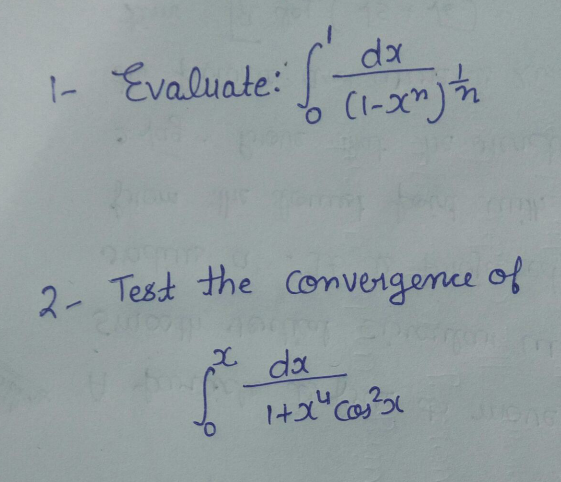
Answered by mathdave last updated on 27/Aug/20
solution to question 1 let I=∫_0 ^1 (dx/((1−x^n )^(1/n) )) let y=x^n , x=y^(1/n) and dx=(1/n)y^((1/n)−1) I=∫_0 ^1 (1/((1−y)))×(1/n)y^((1/n)−1) =(1/n)∫_0 ^1 (y^((1/n)−1) /((1−y)^(1/n) ))dy I=(1/n)∫_0 ^1 y^((1/n)−1) (1−y)^(−(1/n)) =(1/n)∫_0 ^1 y^((1/n)−1) (1−y)^(1−(1/n)) but this has illustrate beta function I=(1/n)β((1/n),1−(1/n))=(1/n)•((Γ((1/n)).Γ(1−(1/n)))/(Γ((1/n)+1−(1/n)))) I=(1/n)•Γ((1/n)).Γ(1−(1/n)) but recall zeta eular idntity which state Γ(x).Γ(1−x)=(π/(sin(πx))) I=(1/n)•Γ((1/n)).Γ(1−(1/n))=(1/n)•(π/(sin((π/n)))) ∵∫_0 ^1 (dx/((1−x^n )^(1/n) ))=(π/n)cosec((π/n)) by mathdave(27/08/2020)
$${solution}\:{to}\:{question}\:\mathrm{1} \\ $$$${let}\:\:{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\left(\mathrm{1}−{x}^{{n}} \right)^{\frac{\mathrm{1}}{{n}}} } \\ $$$${let}\:{y}={x}^{{n}} \:\:,\:{x}={y}^{\frac{\mathrm{1}}{{n}}} \:\:\:{and}\:\:\:{dx}=\frac{\mathrm{1}}{{n}}{y}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{1}−{y}\right)}×\frac{\mathrm{1}}{{n}}{y}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} =\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{y}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} }{\left(\mathrm{1}−{y}\right)^{\frac{\mathrm{1}}{{n}}} }{dy} \\ $$$${I}=\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {y}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \left(\mathrm{1}−{y}\right)^{−\frac{\mathrm{1}}{{n}}} =\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {y}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \left(\mathrm{1}−{y}\right)^{\mathrm{1}−\frac{\mathrm{1}}{{n}}} \\ $$$${but}\:{this}\:{has}\:{illustrate}\:{beta}\:{function} \\ $$$${I}=\frac{\mathrm{1}}{{n}}\beta\left(\frac{\mathrm{1}}{{n}},\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)=\frac{\mathrm{1}}{{n}}\bullet\frac{\Gamma\left(\frac{\mathrm{1}}{{n}}\right).\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)}{\Gamma\left(\frac{\mathrm{1}}{{n}}+\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)} \\ $$$${I}=\frac{\mathrm{1}}{{n}}\bullet\Gamma\left(\frac{\mathrm{1}}{{n}}\right).\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right) \\ $$$${but}\:{recall}\:\:{zeta}\:{eular}\:{idntity}\:{which}\:{state} \\ $$$$\Gamma\left({x}\right).\Gamma\left(\mathrm{1}−{x}\right)=\frac{\pi}{\mathrm{sin}\left(\pi{x}\right)} \\ $$$${I}=\frac{\mathrm{1}}{{n}}\bullet\Gamma\left(\frac{\mathrm{1}}{{n}}\right).\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)=\frac{\mathrm{1}}{{n}}\bullet\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{{n}}\right)} \\ $$$$\because\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\left(\mathrm{1}−{x}^{{n}} \right)^{\frac{\mathrm{1}}{{n}}} }=\frac{\pi}{{n}}\mathrm{cosec}\left(\frac{\pi}{{n}}\right) \\ $$$${by}\:{mathdave}\left(\mathrm{27}/\mathrm{08}/\mathrm{2020}\right) \\ $$
Commented by I want to learn more last updated on 27/Aug/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by mathmax by abdo last updated on 28/Aug/20
A_n =∫_0 ^1 (dx/((1−x^n )^(1/n) )) changement 1−x^n =t give x^n =1−t ⇒ x =(1−t)^(1/n) ⇒ A_n =−∫_0 ^1 t^(−(1/n)) .(1/n)(−1)(1−t)^((1/n)−1) dt =(1/n) ∫_0 ^1 t^(1−(1/n)−1) (1−t)^((1/n)−1) dt =(1/n)B((1/n),1−(1/n)) =(1/n).((Γ((1/n)).Γ(1−(1/n)))/(Γ(1))) =(1/n)Γ((1/n)).Γ(1−(1/n)) we know Γ(x).Γ(1−x) =(π/(sin(πx))) if 0<x<1 (compliment formula) Γ((1/n)).Γ(1−(1/n)) =(π/(sin((π/n)))) ⇒★ A_n =(π/(nsin((π/n))))★
$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{n}} \right)^{\frac{\mathrm{1}}{\mathrm{n}}} }\:\:\mathrm{changement}\:\mathrm{1}−\mathrm{x}^{\mathrm{n}} \:=\mathrm{t}\:\mathrm{give}\:\mathrm{x}^{\mathrm{n}} \:=\mathrm{1}−\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{x}\:=\left(\mathrm{1}−\mathrm{t}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \:\Rightarrow\:\mathrm{A}_{\mathrm{n}} =−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{t}^{−\frac{\mathrm{1}}{\mathrm{n}}} .\frac{\mathrm{1}}{\mathrm{n}}\left(−\mathrm{1}\right)\left(\mathrm{1}−\mathrm{t}\right)^{\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\mathrm{t}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} \:\left(\mathrm{1}−\mathrm{t}\right)^{\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{n}}\mathrm{B}\left(\frac{\mathrm{1}}{\mathrm{n}},\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}}.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{n}}\right).\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}}\right)}{\Gamma\left(\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\mathrm{n}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{n}}\right).\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}}\right) \\ $$$$\mathrm{we}\:\mathrm{know}\:\Gamma\left(\mathrm{x}\right).\Gamma\left(\mathrm{1}−\mathrm{x}\right)\:=\frac{\pi}{\mathrm{sin}\left(\pi\mathrm{x}\right)}\:\:\:\:\:\mathrm{if}\:\mathrm{0}<\mathrm{x}<\mathrm{1}\:\left(\mathrm{compliment}\:\mathrm{formula}\right) \\ $$$$\Gamma\left(\frac{\mathrm{1}}{\mathrm{n}}\right).\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}}\right)\:=\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{n}}\right)}\:\Rightarrow\bigstar\:\mathrm{A}_{\mathrm{n}} =\frac{\pi}{\mathrm{nsin}\left(\frac{\pi}{\mathrm{n}}\right)}\bigstar \\ $$
Commented by I want to learn more last updated on 28/Aug/20
Thanks sir.
$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *