Question Number 110204 by Algoritm last updated on 27/Aug/20
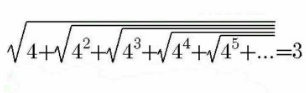
Commented by Algoritm last updated on 27/Aug/20

$$\blacklozenge\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}}\:! \\ $$
Commented by prakash jain last updated on 28/Aug/20
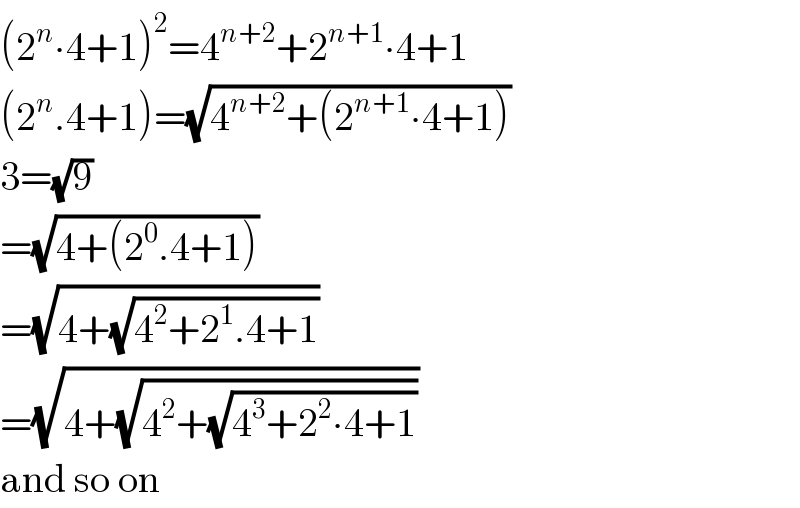
$$\left(\mathrm{2}^{{n}} \centerdot\mathrm{4}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}^{{n}+\mathrm{2}} +\mathrm{2}^{{n}+\mathrm{1}} \centerdot\mathrm{4}+\mathrm{1} \\ $$$$\left(\mathrm{2}^{{n}} .\mathrm{4}+\mathrm{1}\right)=\sqrt{\mathrm{4}^{{n}+\mathrm{2}} +\left(\mathrm{2}^{{n}+\mathrm{1}} \centerdot\mathrm{4}+\mathrm{1}\right)} \\ $$$$\mathrm{3}=\sqrt{\mathrm{9}} \\ $$$$=\sqrt{\mathrm{4}+\left(\mathrm{2}^{\mathrm{0}} .\mathrm{4}+\mathrm{1}\right)} \\ $$$$=\sqrt{\mathrm{4}+\sqrt{\mathrm{4}^{\mathrm{2}} +\mathrm{2}^{\mathrm{1}} .\mathrm{4}+\mathrm{1}}} \\ $$$$=\sqrt{\mathrm{4}+\sqrt{\mathrm{4}^{\mathrm{2}} +\sqrt{\mathrm{4}^{\mathrm{3}} +\mathrm{2}^{\mathrm{2}} \centerdot\mathrm{4}+\mathrm{1}}}} \\ $$$$\mathrm{and}\:\mathrm{so}\:\mathrm{on} \\ $$
Commented by Algoritm last updated on 27/Aug/20
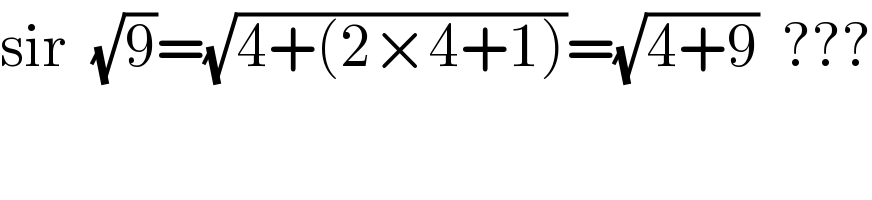
$$\mathrm{sir}\:\:\sqrt{\mathrm{9}}=\sqrt{\mathrm{4}+\left(\mathrm{2}×\mathrm{4}+\mathrm{1}\right)}=\sqrt{\mathrm{4}+\mathrm{9}}\:\:??? \\ $$
Commented by prakash jain last updated on 28/Aug/20
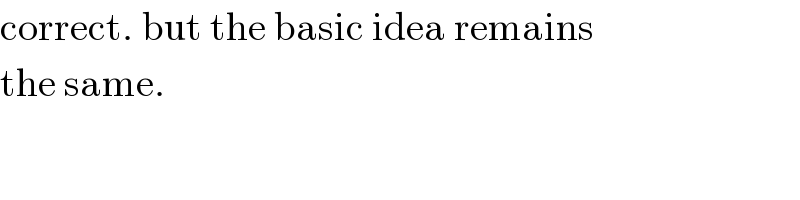
$$\mathrm{correct}.\:\mathrm{but}\:\mathrm{the}\:\mathrm{basic}\:\mathrm{idea}\:\mathrm{remains} \\ $$$$\mathrm{the}\:\mathrm{same}. \\ $$
Answered by Dwaipayan Shikari last updated on 27/Aug/20
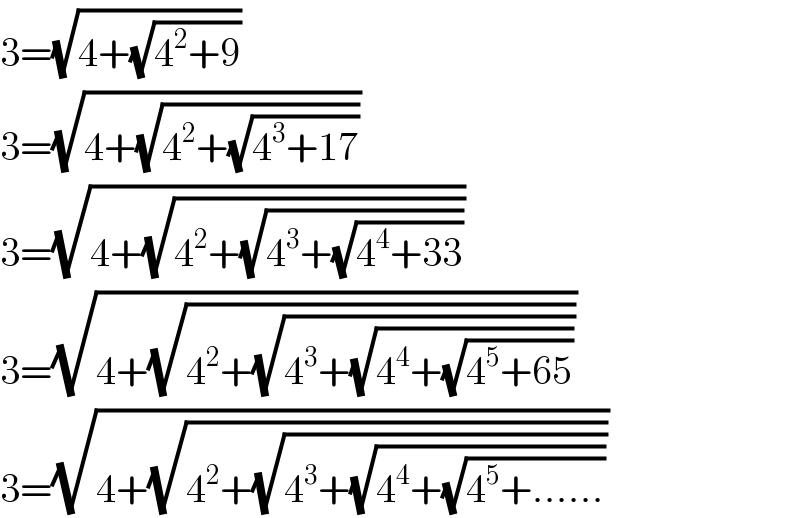
$$\mathrm{3}=\sqrt{\mathrm{4}+\sqrt{\mathrm{4}^{\mathrm{2}} +\mathrm{9}}} \\ $$$$\mathrm{3}=\sqrt{\mathrm{4}+\sqrt{\mathrm{4}^{\mathrm{2}} +\sqrt{\mathrm{4}^{\mathrm{3}} +\mathrm{17}}}} \\ $$$$\mathrm{3}=\sqrt{\mathrm{4}+\sqrt{\mathrm{4}^{\mathrm{2}} +\sqrt{\mathrm{4}^{\mathrm{3}} +\sqrt{\mathrm{4}^{\mathrm{4}} +\mathrm{33}}}}} \\ $$$$\mathrm{3}=\sqrt{\mathrm{4}+\sqrt{\mathrm{4}^{\mathrm{2}} +\sqrt{\mathrm{4}^{\mathrm{3}} +\sqrt{\mathrm{4}^{\mathrm{4}} +\sqrt{\mathrm{4}^{\mathrm{5}} +\mathrm{65}}}}}} \\ $$$$\mathrm{3}=\sqrt{\mathrm{4}+\sqrt{\mathrm{4}^{\mathrm{2}} +\sqrt{\mathrm{4}^{\mathrm{3}} +\sqrt{\mathrm{4}^{\mathrm{4}} +\sqrt{\mathrm{4}^{\mathrm{5}} +……}}}}} \\ $$
