Question Number 110215 by 150505R last updated on 27/Aug/20
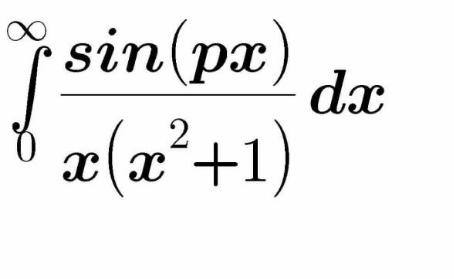
Commented by 150505R last updated on 27/Aug/20

$${please}\:{solve}… \\ $$
Answered by mathmax by abdo last updated on 27/Aug/20
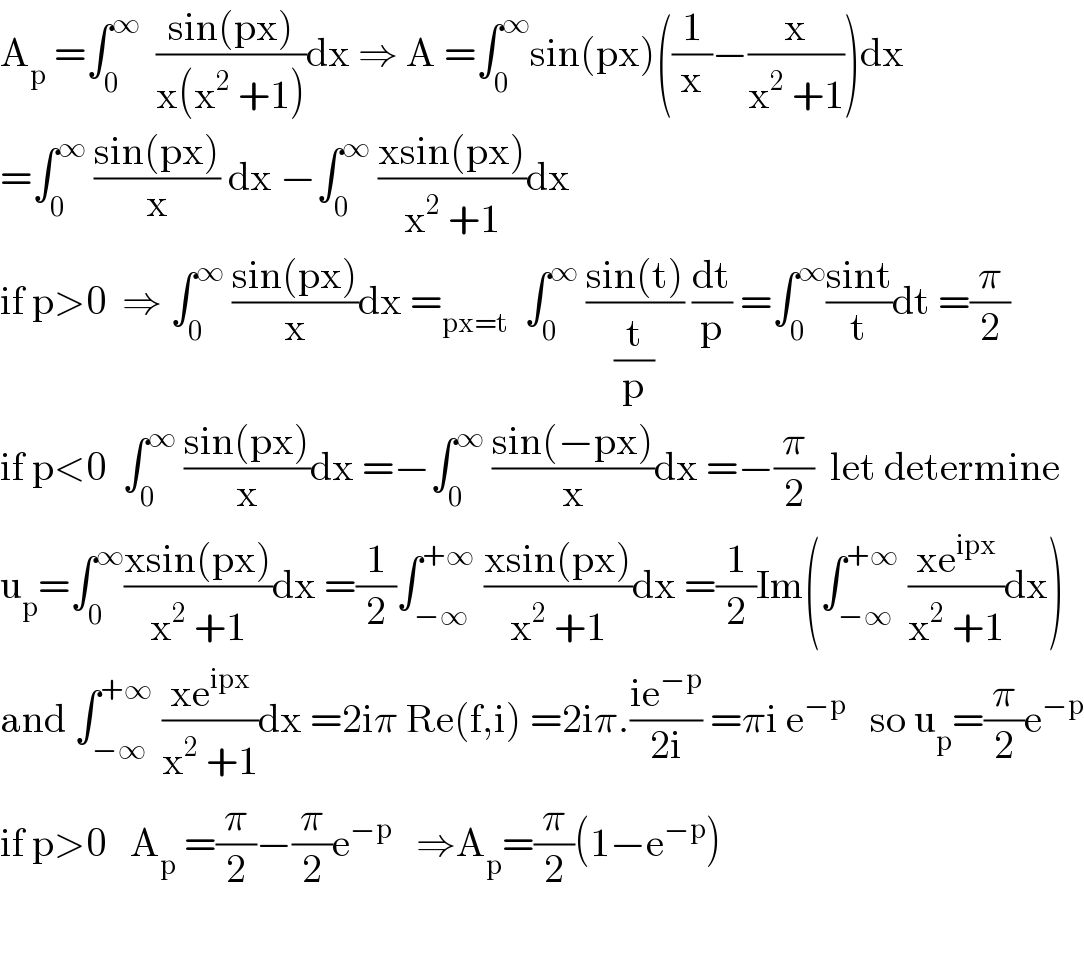
$$\mathrm{A}_{\mathrm{p}} \:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{sin}\left(\mathrm{px}\right)}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dx}\:\Rightarrow\:\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \mathrm{sin}\left(\mathrm{px}\right)\left(\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{px}\right)}{\mathrm{x}}\:\mathrm{dx}\:−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{xsin}\left(\mathrm{px}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx} \\ $$$$\mathrm{if}\:\mathrm{p}>\mathrm{0}\:\:\Rightarrow\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{px}\right)}{\mathrm{x}}\mathrm{dx}\:=_{\mathrm{px}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{t}\right)}{\frac{\mathrm{t}}{\mathrm{p}}}\:\frac{\mathrm{dt}}{\mathrm{p}}\:=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sint}}{\mathrm{t}}\mathrm{dt}\:=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{if}\:\mathrm{p}<\mathrm{0}\:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{px}\right)}{\mathrm{x}}\mathrm{dx}\:=−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(−\mathrm{px}\right)}{\mathrm{x}}\mathrm{dx}\:=−\frac{\pi}{\mathrm{2}}\:\:\mathrm{let}\:\mathrm{determine} \\ $$$$\mathrm{u}_{\mathrm{p}} =\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{xsin}\left(\mathrm{px}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{xsin}\left(\mathrm{px}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Im}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{xe}^{\mathrm{ipx}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\right) \\ $$$$\mathrm{and}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{xe}^{\mathrm{ipx}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\mathrm{2i}\pi\:\mathrm{Re}\left(\mathrm{f},\mathrm{i}\right)\:=\mathrm{2i}\pi.\frac{\mathrm{ie}^{−\mathrm{p}} }{\mathrm{2i}}\:=\pi\mathrm{i}\:\mathrm{e}^{−\mathrm{p}} \:\:\:\mathrm{so}\:\mathrm{u}_{\mathrm{p}} =\frac{\pi}{\mathrm{2}}\mathrm{e}^{−\mathrm{p}} \\ $$$$\mathrm{if}\:\mathrm{p}>\mathrm{0}\:\:\:\mathrm{A}_{\mathrm{p}} \:=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{2}}\mathrm{e}^{−\mathrm{p}} \:\:\:\Rightarrow\mathrm{A}_{\mathrm{p}} =\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\mathrm{e}^{−\mathrm{p}} \right) \\ $$$$ \\ $$
