Menu Close

Question-110287

Tinku Tara 0 Comments
Pin




Question Number 110287 by mathdave last updated on 28/Aug/20
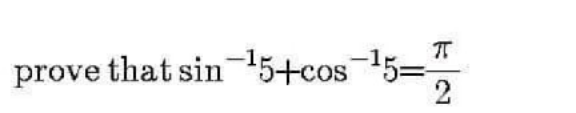
Commented by bemath last updated on 28/Aug/20
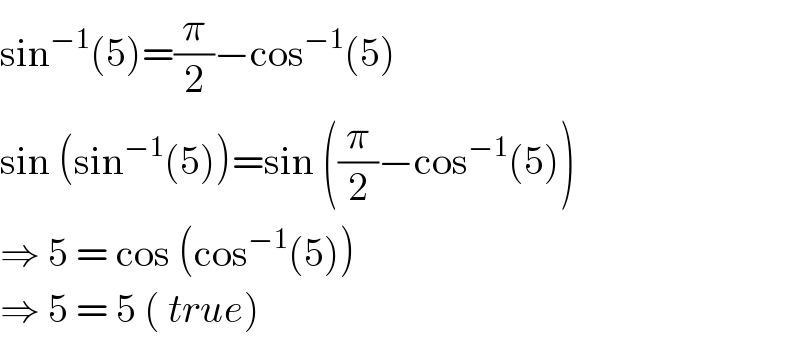
sin^(−1) (5)=(π/2)−cos^(−1) (5) sin (sin^(−1) (5))=sin ((π/2)−cos^(−1) (5)) ⇒ 5 = cos (cos^(−1) (5)) ⇒ 5 = 5 ( true)
$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{5}\right)=\frac{\pi}{\mathrm{2}}−\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{5}\right) \\ $$$$\mathrm{sin}\:\left(\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{5}\right)\right)=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{5}\right)\right) \\ $$$$\Rightarrow\:\mathrm{5}\:=\:\mathrm{cos}\:\left(\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{5}\right)\right) \\ $$$$\Rightarrow\:\mathrm{5}\:=\:\mathrm{5}\:\left(\:{true}\right) \\ $$
Commented by udaythool last updated on 28/Aug/20
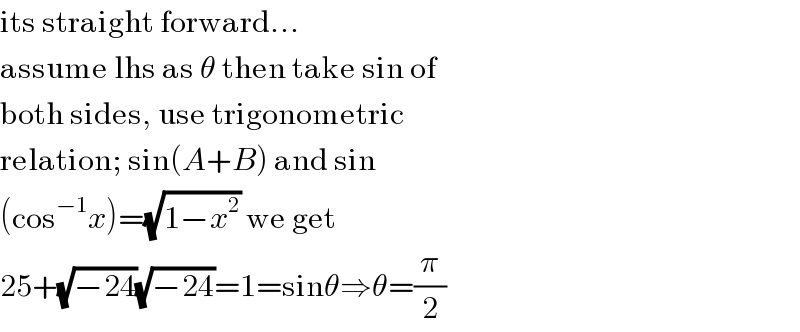
its straight forward... assume lhs as θ then take sin of both sides, use trigonometric relation; sin(A+B) and sin (cos^(−1) x)=(√(1−x^2 )) we get 25+(√(−24))(√(−24))=1=sinθ⇒θ=(π/2)
$$\mathrm{its}\:\mathrm{straight}\:\mathrm{forward}… \\ $$$$\mathrm{assume}\:\mathrm{lhs}\:\mathrm{as}\:\theta\:\mathrm{then}\:\mathrm{take}\:\mathrm{sin}\:\mathrm{of} \\ $$$$\mathrm{both}\:\mathrm{sides},\:\mathrm{use}\:\mathrm{trigonometric} \\ $$$$\mathrm{relation};\:\mathrm{sin}\left({A}+{B}\right)\:\mathrm{and}\:\mathrm{sin} \\ $$$$\left(\mathrm{cos}^{−\mathrm{1}} {x}\right)=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{25}+\sqrt{−\mathrm{24}}\sqrt{−\mathrm{24}}=\mathrm{1}=\mathrm{sin}\theta\Rightarrow\theta=\frac{\pi}{\mathrm{2}} \\ $$
Answered by $@y@m last updated on 28/Aug/20
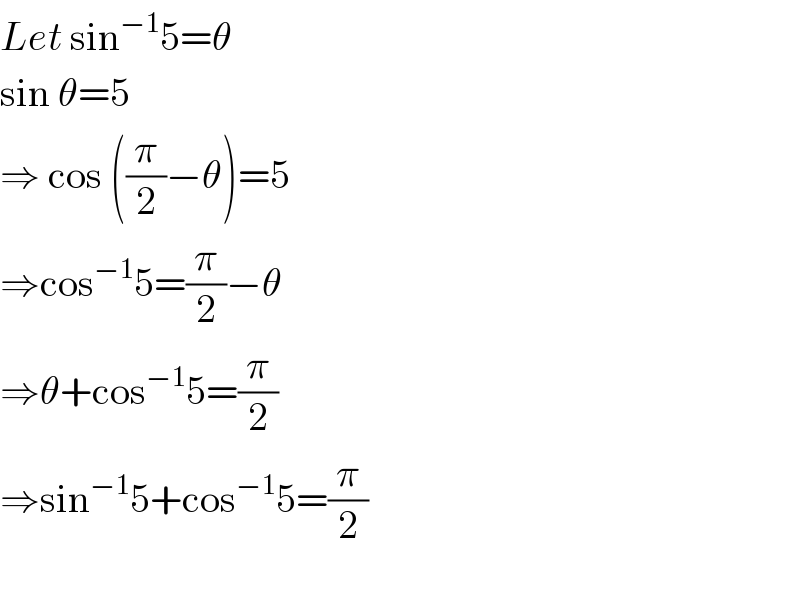
Let sin^(−1) 5=θ sin θ=5 ⇒ cos ((π/2)−θ)=5 ⇒cos^(−1) 5=(π/2)−θ ⇒θ+cos^(−1) 5=(π/2) ⇒sin^(−1) 5+cos^(−1) 5=(π/2)
$${Let}\:\mathrm{sin}^{−\mathrm{1}} \mathrm{5}=\theta \\ $$$$\mathrm{sin}\:\theta=\mathrm{5} \\ $$$$\Rightarrow\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\theta\right)=\mathrm{5} \\ $$$$\Rightarrow\mathrm{cos}^{−\mathrm{1}} \mathrm{5}=\frac{\pi}{\mathrm{2}}−\theta \\ $$$$\Rightarrow\theta+\mathrm{cos}^{−\mathrm{1}} \mathrm{5}=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}^{−\mathrm{1}} \mathrm{5}+\mathrm{cos}^{−\mathrm{1}} \mathrm{5}=\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$
Commented by $@y@m last updated on 28/Aug/20
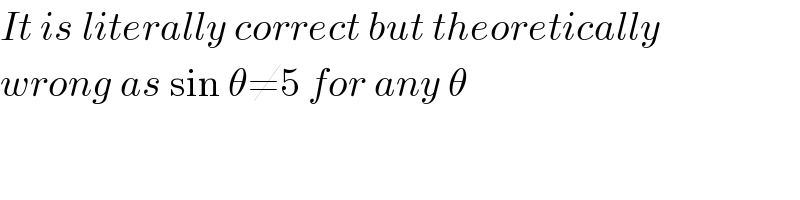
It is literally correct but theoretically wrong as sin θ≠5 for any θ
$${It}\:{is}\:{literally}\:{correct}\:{but}\:{theoretically} \\ $$$${wrong}\:{as}\:\mathrm{sin}\:\theta\neq\mathrm{5}\:{for}\:{any}\:\theta \\ $$
Answered by Her_Majesty last updated on 28/Aug/20
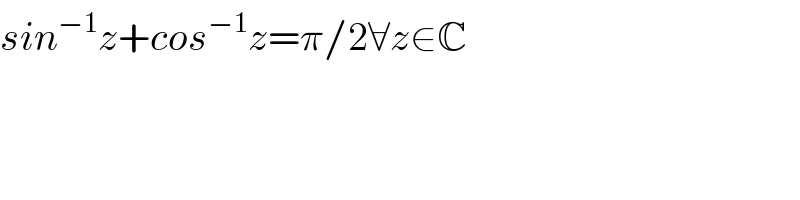
sin^(−1) z+cos^(−1) z=π/2∀z∈C
$${sin}^{−\mathrm{1}} {z}+{cos}^{−\mathrm{1}} {z}=\pi/\mathrm{2}\forall{z}\in\mathbb{C} \\ $$
Commented by $@y@m last updated on 28/Aug/20
Commented by Her_Majesty last updated on 28/Aug/20
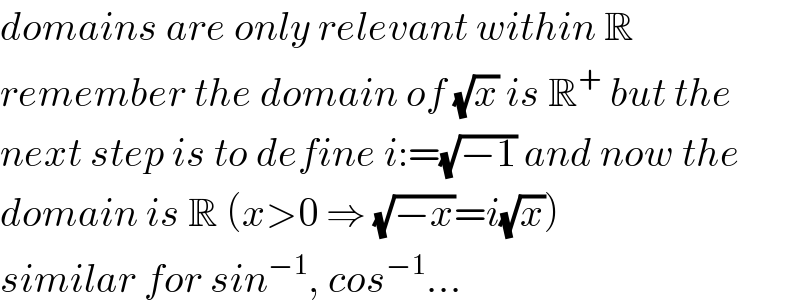
domains are only relevant within R remember the domain of (√x) is R^+ but the next step is to define i:=(√(−1)) and now the domain is R (x>0 ⇒ (√(−x))=i(√x)) similar for sin^(−1) , cos^(−1) ...
$${domains}\:{are}\:{only}\:{relevant}\:{within}\:\mathbb{R} \\ $$$${remember}\:{the}\:{domain}\:{of}\:\sqrt{{x}}\:{is}\:\mathbb{R}^{+} \:{but}\:{the} \\ $$$${next}\:{step}\:{is}\:{to}\:{define}\:{i}:=\sqrt{−\mathrm{1}}\:{and}\:{now}\:{the} \\ $$$${domain}\:{is}\:\mathbb{R}\:\left({x}>\mathrm{0}\:\Rightarrow\:\sqrt{−{x}}={i}\sqrt{{x}}\right) \\ $$$${similar}\:{for}\:{sin}^{−\mathrm{1}} ,\:{cos}^{−\mathrm{1}} … \\ $$
Commented by $@y@m last updated on 29/Aug/20
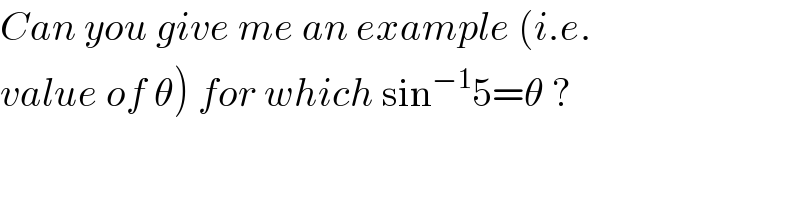
Can you give me an example (i.e. value of θ) for which sin^(−1) 5=θ ?
$${Can}\:{you}\:{give}\:{me}\:{an}\:{example}\:\left({i}.{e}.\right. \\ $$$$\left.{value}\:{of}\:\theta\right)\:{for}\:{which}\:\mathrm{sin}^{−\mathrm{1}} \mathrm{5}=\theta\:? \\ $$
Commented by Her_Majesty last updated on 29/Aug/20
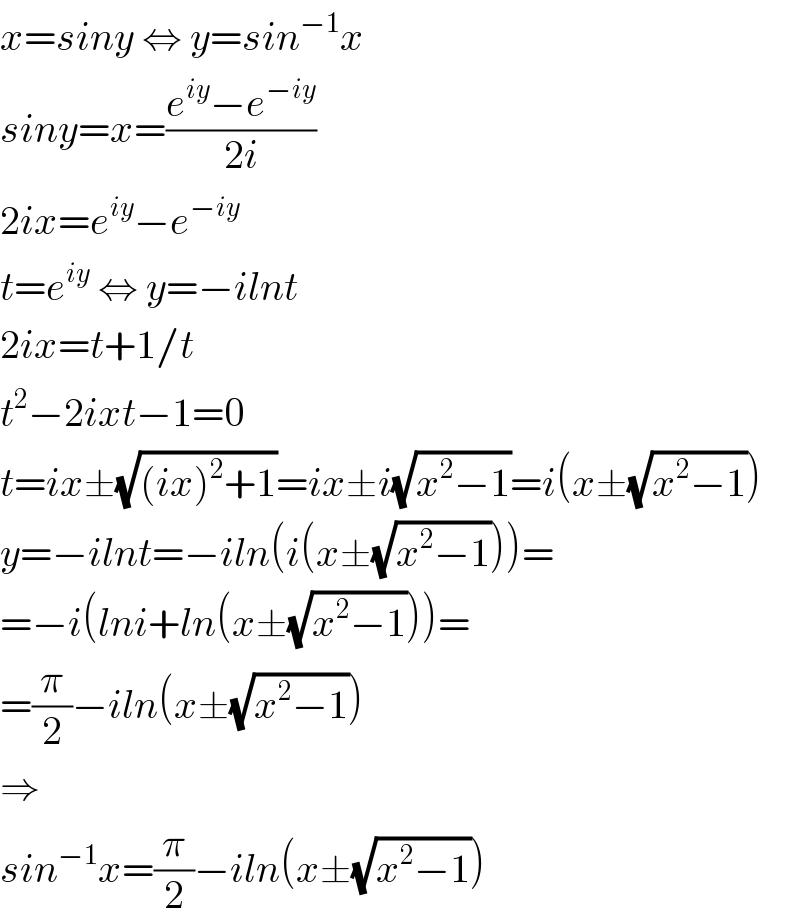
x=siny ⇔ y=sin^(−1) x siny=x=((e^(iy) −e^(−iy) )/(2i)) 2ix=e^(iy) −e^(−iy) t=e^(iy) ⇔ y=−ilnt 2ix=t+1/t t^2 −2ixt−1=0 t=ix±(√((ix)^2 +1))=ix±i(√(x^2 −1))=i(x±(√(x^2 −1))) y=−ilnt=−iln(i(x±(√(x^2 −1))))= =−i(lni+ln(x±(√(x^2 −1))))= =(π/2)−iln(x±(√(x^2 −1))) ⇒ sin^(−1) x=(π/2)−iln(x±(√(x^2 −1)))
$${x}={siny}\:\Leftrightarrow\:{y}={sin}^{−\mathrm{1}} {x} \\ $$$${siny}={x}=\frac{{e}^{{iy}} −{e}^{−{iy}} }{\mathrm{2}{i}} \\ $$$$\mathrm{2}{ix}={e}^{{iy}} −{e}^{−{iy}} \\ $$$${t}={e}^{{iy}} \:\Leftrightarrow\:{y}=−{ilnt} \\ $$$$\mathrm{2}{ix}={t}+\mathrm{1}/{t} \\ $$$${t}^{\mathrm{2}} −\mathrm{2}{ixt}−\mathrm{1}=\mathrm{0} \\ $$$${t}={ix}\pm\sqrt{\left({ix}\right)^{\mathrm{2}} +\mathrm{1}}={ix}\pm{i}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}={i}\left({x}\pm\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$${y}=−{ilnt}=−{iln}\left({i}\left({x}\pm\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)\right)= \\ $$$$=−{i}\left({lni}+{ln}\left({x}\pm\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)\right)= \\ $$$$=\frac{\pi}{\mathrm{2}}−{iln}\left({x}\pm\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$\Rightarrow \\ $$$${sin}^{−\mathrm{1}} {x}=\frac{\pi}{\mathrm{2}}−{iln}\left({x}\pm\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$
Commented by Her_Majesty last updated on 29/Aug/20
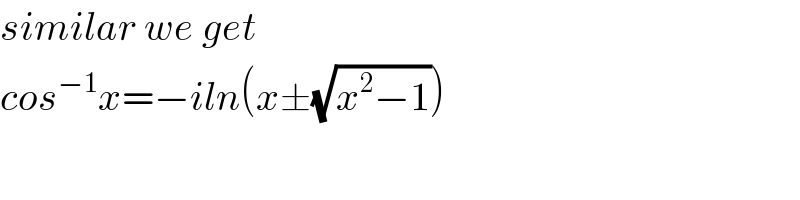
similar we get cos^(−1) x=−iln(x±(√(x^2 −1)))
$${similar}\:{we}\:{get} \\ $$$${cos}^{−\mathrm{1}} {x}=−{iln}\left({x}\pm\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$
Answered by 1549442205PVT last updated on 29/Aug/20
Put ϕ=sin^(−1) 5,cos^(−1) 5=θ we have sinϕ=5,cosθ=5⇒sinϕ=cosθ ⇔sinϕ=sin((π/2)−θ)⇒ϕ=(π/2)−θ+2kπ ⇔ϕ+θ=(π/2)+2kπ But bythe definition of the function sin^(−1) (x) , cos^(−1) (x)we have ((−π)/2)≤ϕ≤(π/2), and 0≤θ≤π Hence ((−π)/2)≤ϕ+θ≤((3π)/2),so −(π/2)≤ϕ+θ=(π/2)+2kπ≤((3π)/2)⇒k=0 ⇒𝛟+𝛉=(𝛑/2)⇒sin^(−1) 5+cos^(−1) 5=(𝛑/2)(Q.E.D)
$$\mathrm{Put}\:\varphi=\mathrm{sin}^{−\mathrm{1}} \mathrm{5},\mathrm{cos}^{−\mathrm{1}} \mathrm{5}=\theta\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{sin}\varphi=\mathrm{5},\mathrm{cos}\theta=\mathrm{5}\Rightarrow\mathrm{sin}\varphi=\mathrm{cos}\theta \\ $$$$\Leftrightarrow\mathrm{sin}\varphi=\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}−\theta\right)\Rightarrow\varphi=\frac{\pi}{\mathrm{2}}−\theta+\mathrm{2k}\pi \\ $$$$\Leftrightarrow\varphi+\theta=\frac{\pi}{\mathrm{2}}+\mathrm{2k}\pi \\ $$$$\mathrm{But}\:\mathrm{bythe}\:\mathrm{definition}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function} \\ $$$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}\right)\:,\:\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{x}\right)\mathrm{we}\:\mathrm{have}\:\frac{−\pi}{\mathrm{2}}\leqslant\varphi\leqslant\frac{\pi}{\mathrm{2}}, \\ $$$$\mathrm{and}\:\mathrm{0}\leqslant\theta\leqslant\pi\:\mathrm{Hence}\:\frac{−\pi}{\mathrm{2}}\leqslant\varphi+\theta\leqslant\frac{\mathrm{3}\pi}{\mathrm{2}},\mathrm{so} \\ $$$$−\frac{\pi}{\mathrm{2}}\leqslant\varphi+\theta=\frac{\pi}{\mathrm{2}}+\mathrm{2k}\pi\leqslant\frac{\mathrm{3}\pi}{\mathrm{2}}\Rightarrow\mathrm{k}=\mathrm{0} \\ $$$$\Rightarrow\boldsymbol{\varphi}+\boldsymbol{\theta}=\frac{\boldsymbol{\pi}}{\mathrm{2}}\Rightarrow\boldsymbol{\mathrm{sin}}^{−\mathrm{1}} \mathrm{5}+\boldsymbol{\mathrm{cos}}^{−\mathrm{1}} \mathrm{5}=\frac{\boldsymbol{\pi}}{\mathrm{2}}\left(\boldsymbol{\mathrm{Q}}.\boldsymbol{\mathrm{E}}.\boldsymbol{\mathrm{D}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *