Menu Close

Question-110365

Tinku Tara 0 Comments
Pin




Question Number 110365 by mathdave last updated on 28/Aug/20
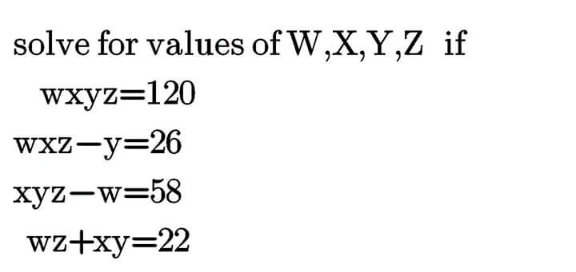
Answered by Rasheed.Sindhi last updated on 29/Aug/20
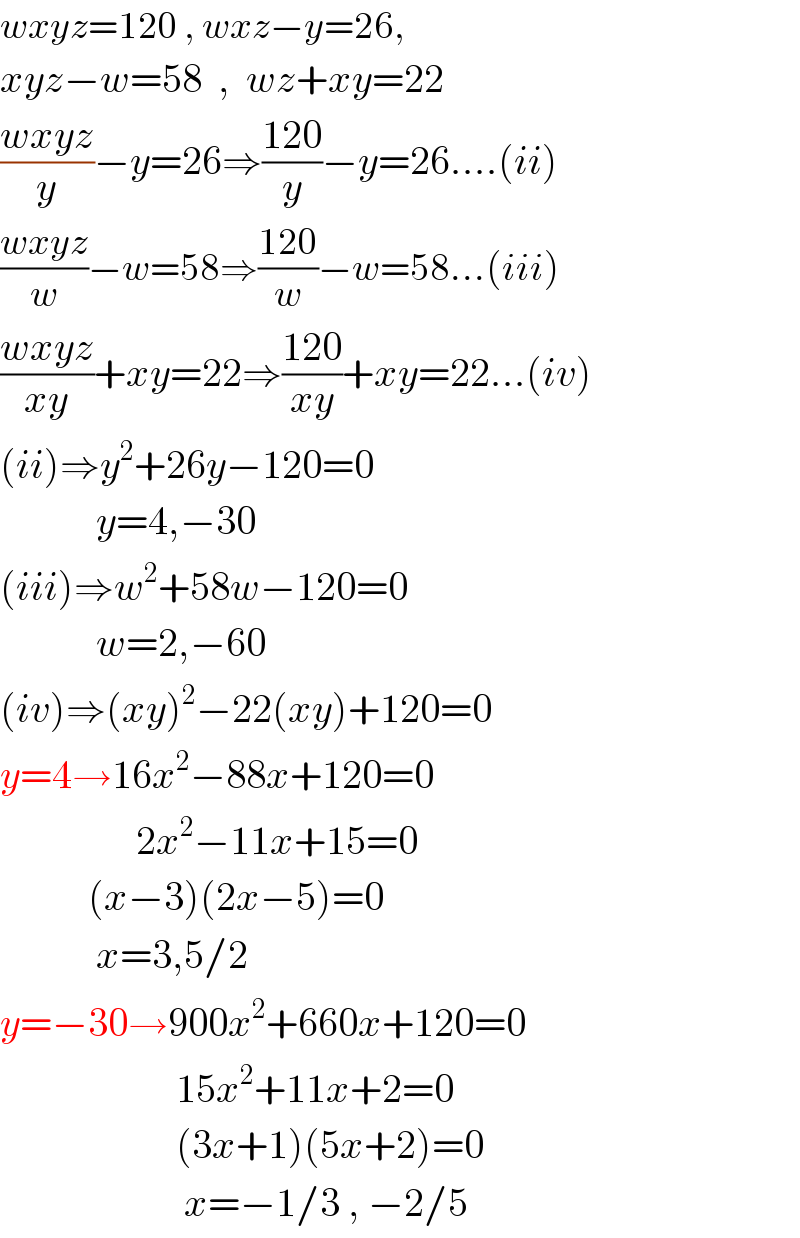
wxyz=120 , wxz−y=26, xyz−w=58 , wz+xy=22 ((wxyz)/y)−y=26⇒((120)/y)−y=26....(ii) ((wxyz)/w)−w=58⇒((120)/w)−w=58...(iii) ((wxyz)/(xy))+xy=22⇒((120)/(xy))+xy=22...(iv) (ii)⇒y^2 +26y−120=0 y=4,−30 (iii)⇒w^2 +58w−120=0 w=2,−60 (iv)⇒(xy)^2 −22(xy)+120=0 y=4→16x^2 −88x+120=0 2x^2 −11x+15=0 (x−3)(2x−5)=0 x=3,5/2 y=−30→900x^2 +660x+120=0 15x^2 +11x+2=0 (3x+1)(5x+2)=0 x=−1/3 , −2/5
$${wxyz}=\mathrm{120}\:,\:{wxz}−{y}=\mathrm{26}, \\ $$$${xyz}−{w}=\mathrm{58}\:\:,\:\:{wz}+{xy}=\mathrm{22} \\ $$$$\frac{{wxyz}}{{y}}−{y}=\mathrm{26}\Rightarrow\frac{\mathrm{120}}{{y}}−{y}=\mathrm{26}….\left({ii}\right) \\ $$$$\frac{{wxyz}}{{w}}−{w}=\mathrm{58}\Rightarrow\frac{\mathrm{120}}{{w}}−{w}=\mathrm{58}…\left({iii}\right) \\ $$$$\frac{{wxyz}}{{xy}}+{xy}=\mathrm{22}\Rightarrow\frac{\mathrm{120}}{{xy}}+{xy}=\mathrm{22}…\left({iv}\right) \\ $$$$\left({ii}\right)\Rightarrow{y}^{\mathrm{2}} +\mathrm{26}{y}−\mathrm{120}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{y}=\mathrm{4},−\mathrm{30} \\ $$$$\left({iii}\right)\Rightarrow{w}^{\mathrm{2}} +\mathrm{58}{w}−\mathrm{120}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{w}=\mathrm{2},−\mathrm{60} \\ $$$$\left({iv}\right)\Rightarrow\left({xy}\right)^{\mathrm{2}} −\mathrm{22}\left({xy}\right)+\mathrm{120}=\mathrm{0} \\ $$$${y}=\mathrm{4}\rightarrow\mathrm{16}{x}^{\mathrm{2}} −\mathrm{88}{x}+\mathrm{120}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{x}^{\mathrm{2}} −\mathrm{11}{x}+\mathrm{15}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left({x}−\mathrm{3}\right)\left(\mathrm{2}{x}−\mathrm{5}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{x}=\mathrm{3},\mathrm{5}/\mathrm{2} \\ $$$${y}=−\mathrm{30}\rightarrow\mathrm{900}{x}^{\mathrm{2}} +\mathrm{660}{x}+\mathrm{120}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{15}{x}^{\mathrm{2}} +\mathrm{11}{x}+\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{3}{x}+\mathrm{1}\right)\left(\mathrm{5}{x}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}=−\mathrm{1}/\mathrm{3}\:,\:−\mathrm{2}/\mathrm{5} \\ $$
Answered by kkc last updated on 28/Aug/20
W=2 X=3 Y=4 z=5
$${W}=\mathrm{2}\:{X}=\mathrm{3}\:{Y}=\mathrm{4}\:{z}=\mathrm{5} \\ $$
Answered by 1549442205PVT last updated on 29/Aug/20
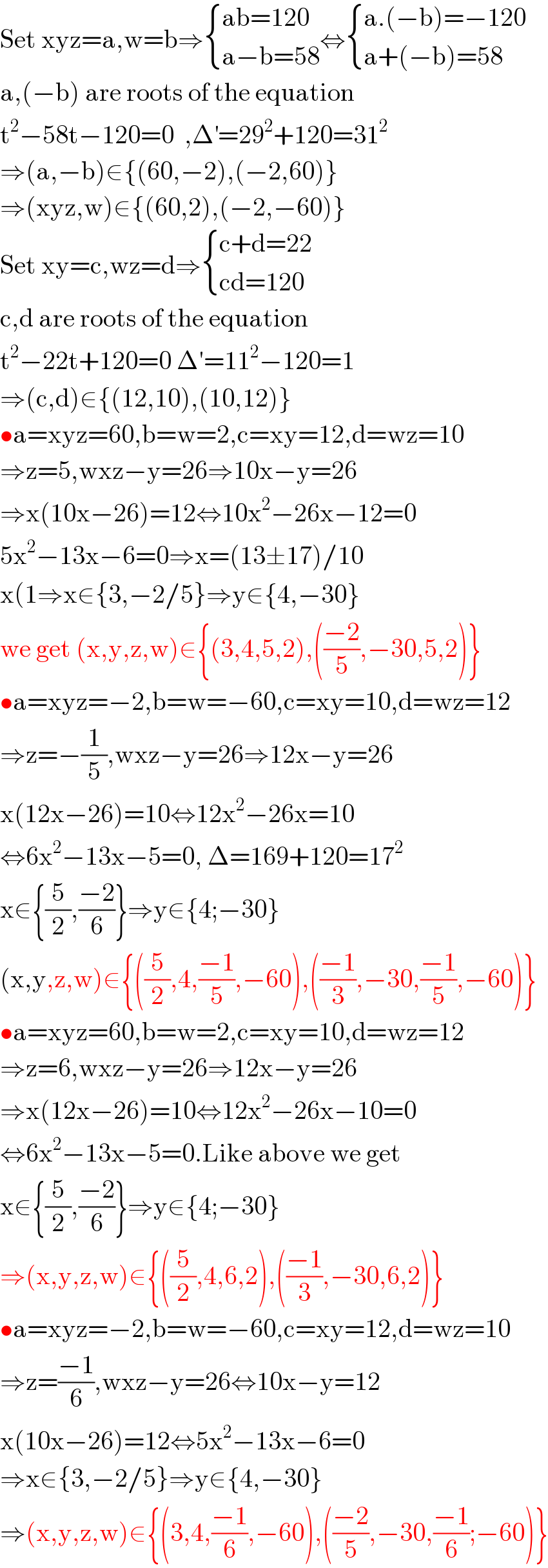
Set xyz=a,w=b⇒ { ((ab=120)),((a−b=58)) :}⇔ { ((a.(−b)=−120)),((a+(−b)=58)) :} a,(−b) are roots of the equation t^2 −58t−120=0 ,Δ^′ =29^2 +120=31^2 ⇒(a,−b)∈{(60,−2),(−2,60)} ⇒(xyz,w)∈{(60,2),(−2,−60)} Set xy=c,wz=d⇒ { ((c+d=22)),((cd=120)) :} c,d are roots of the equation t^2 −22t+120=0 Δ′=11^2 −120=1 ⇒(c,d)∈{(12,10),(10,12)} •a=xyz=60,b=w=2,c=xy=12,d=wz=10 ⇒z=5,wxz−y=26⇒10x−y=26 ⇒x(10x−26)=12⇔10x^2 −26x−12=0 5x^2 −13x−6=0⇒x=(13±17)/10 x(1⇒x∈{3,−2/5}⇒y∈{4,−30} we get (x,y,z,w)∈{(3,4,5,2),(((−2)/5),−30,5,2)} •a=xyz=−2,b=w=−60,c=xy=10,d=wz=12 ⇒z=−(1/5),wxz−y=26⇒12x−y=26 x(12x−26)=10⇔12x^2 −26x=10 ⇔6x^2 −13x−5=0, Δ=169+120=17^2 x∈{(5/2),((−2)/6)}⇒y∈{4;−30} (x,y,z,w)∈{((5/2),4,((−1)/5),−60),(((−1)/3),−30,((−1)/5),−60)} •a=xyz=60,b=w=2,c=xy=10,d=wz=12 ⇒z=6,wxz−y=26⇒12x−y=26 ⇒x(12x−26)=10⇔12x^2 −26x−10=0 ⇔6x^2 −13x−5=0.Like above we get x∈{(5/2),((−2)/6)}⇒y∈{4;−30} ⇒(x,y,z,w)∈{((5/2),4,6,2),(((−1)/3),−30,6,2)} •a=xyz=−2,b=w=−60,c=xy=12,d=wz=10 ⇒z=((−1)/6),wxz−y=26⇔10x−y=12 x(10x−26)=12⇔5x^2 −13x−6=0 ⇒x∈{3,−2/5}⇒y∈{4,−30} ⇒(x,y,z,w)∈{(3,4,((−1)/6),−60),(((−2)/5),−30,((−1)/6);−60)}
$$\mathrm{Set}\:\mathrm{xyz}=\mathrm{a},\mathrm{w}=\mathrm{b}\Rightarrow\begin{cases}{\mathrm{ab}=\mathrm{120}}\\{\mathrm{a}−\mathrm{b}=\mathrm{58}}\end{cases}\Leftrightarrow\begin{cases}{\mathrm{a}.\left(−\mathrm{b}\right)=−\mathrm{120}}\\{\mathrm{a}+\left(−\mathrm{b}\right)=\mathrm{58}}\end{cases} \\ $$$$\mathrm{a},\left(−\mathrm{b}\right)\:\mathrm{are}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{t}^{\mathrm{2}} −\mathrm{58t}−\mathrm{120}=\mathrm{0}\:\:,\Delta^{'} =\mathrm{29}^{\mathrm{2}} +\mathrm{120}=\mathrm{31}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{a},−\mathrm{b}\right)\in\left\{\left(\mathrm{60},−\mathrm{2}\right),\left(−\mathrm{2},\mathrm{60}\right)\right\} \\ $$$$\Rightarrow\left(\mathrm{xyz},\mathrm{w}\right)\in\left\{\left(\mathrm{60},\mathrm{2}\right),\left(−\mathrm{2},−\mathrm{60}\right)\right\} \\ $$$$\mathrm{Set}\:\mathrm{xy}=\mathrm{c},\mathrm{wz}=\mathrm{d}\Rightarrow\begin{cases}{\mathrm{c}+\mathrm{d}=\mathrm{22}}\\{\mathrm{cd}=\mathrm{120}}\end{cases} \\ $$$$\mathrm{c},\mathrm{d}\:\mathrm{are}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{t}^{\mathrm{2}} −\mathrm{22t}+\mathrm{120}=\mathrm{0}\:\Delta'=\mathrm{11}^{\mathrm{2}} −\mathrm{120}=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{c},\mathrm{d}\right)\in\left\{\left(\mathrm{12},\mathrm{10}\right),\left(\mathrm{10},\mathrm{12}\right)\right\} \\ $$$$\bullet\mathrm{a}=\mathrm{xyz}=\mathrm{60},\mathrm{b}=\mathrm{w}=\mathrm{2},\mathrm{c}=\mathrm{xy}=\mathrm{12},\mathrm{d}=\mathrm{wz}=\mathrm{10} \\ $$$$\Rightarrow\mathrm{z}=\mathrm{5},\mathrm{wxz}−\mathrm{y}=\mathrm{26}\Rightarrow\mathrm{10x}−\mathrm{y}=\mathrm{26} \\ $$$$\Rightarrow\mathrm{x}\left(\mathrm{10x}−\mathrm{26}\right)=\mathrm{12}\Leftrightarrow\mathrm{10x}^{\mathrm{2}} −\mathrm{26x}−\mathrm{12}=\mathrm{0} \\ $$$$\mathrm{5x}^{\mathrm{2}} −\mathrm{13x}−\mathrm{6}=\mathrm{0}\Rightarrow\mathrm{x}=\left(\mathrm{13}\pm\mathrm{17}\right)/\mathrm{10} \\ $$$$\mathrm{x}\left(\mathrm{1}\Rightarrow\mathrm{x}\in\left\{\mathrm{3},−\mathrm{2}/\mathrm{5}\right\}\Rightarrow\mathrm{y}\in\left\{\mathrm{4},−\mathrm{30}\right\}\right. \\ $$$$\mathrm{we}\:\mathrm{get}\:\left(\mathrm{x},\mathrm{y},\mathrm{z},\mathrm{w}\right)\in\left\{\left(\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{2}\right),\left(\frac{−\mathrm{2}}{\mathrm{5}},−\mathrm{30},\mathrm{5},\mathrm{2}\right)\right\} \\ $$$$\bullet\mathrm{a}=\mathrm{xyz}=−\mathrm{2},\mathrm{b}=\mathrm{w}=−\mathrm{60},\mathrm{c}=\mathrm{xy}=\mathrm{10},\mathrm{d}=\mathrm{wz}=\mathrm{12} \\ $$$$\Rightarrow\mathrm{z}=−\frac{\mathrm{1}}{\mathrm{5}},\mathrm{wxz}−\mathrm{y}=\mathrm{26}\Rightarrow\mathrm{12x}−\mathrm{y}=\mathrm{26} \\ $$$$\mathrm{x}\left(\mathrm{12x}−\mathrm{26}\right)=\mathrm{10}\Leftrightarrow\mathrm{12x}^{\mathrm{2}} −\mathrm{26x}=\mathrm{10} \\ $$$$\Leftrightarrow\mathrm{6x}^{\mathrm{2}} −\mathrm{13x}−\mathrm{5}=\mathrm{0},\:\Delta=\mathrm{169}+\mathrm{120}=\mathrm{17}^{\mathrm{2}} \\ $$$$\mathrm{x}\in\left\{\frac{\mathrm{5}}{\mathrm{2}},\frac{−\mathrm{2}}{\mathrm{6}}\right\}\Rightarrow\mathrm{y}\in\left\{\mathrm{4};−\mathrm{30}\right\} \\ $$$$\left(\mathrm{x},\mathrm{y},\mathrm{z},\mathrm{w}\right)\in\left\{\left(\frac{\mathrm{5}}{\mathrm{2}},\mathrm{4},\frac{−\mathrm{1}}{\mathrm{5}},−\mathrm{60}\right),\left(\frac{−\mathrm{1}}{\mathrm{3}},−\mathrm{30},\frac{−\mathrm{1}}{\mathrm{5}},−\mathrm{60}\right)\right\} \\ $$$$\bullet\mathrm{a}=\mathrm{xyz}=\mathrm{60},\mathrm{b}=\mathrm{w}=\mathrm{2},\mathrm{c}=\mathrm{xy}=\mathrm{10},\mathrm{d}=\mathrm{wz}=\mathrm{12} \\ $$$$\Rightarrow\mathrm{z}=\mathrm{6},\mathrm{wxz}−\mathrm{y}=\mathrm{26}\Rightarrow\mathrm{12x}−\mathrm{y}=\mathrm{26} \\ $$$$\Rightarrow\mathrm{x}\left(\mathrm{12x}−\mathrm{26}\right)=\mathrm{10}\Leftrightarrow\mathrm{12x}^{\mathrm{2}} −\mathrm{26x}−\mathrm{10}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{6x}^{\mathrm{2}} −\mathrm{13x}−\mathrm{5}=\mathrm{0}.\mathrm{Like}\:\mathrm{above}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{x}\in\left\{\frac{\mathrm{5}}{\mathrm{2}},\frac{−\mathrm{2}}{\mathrm{6}}\right\}\Rightarrow\mathrm{y}\in\left\{\mathrm{4};−\mathrm{30}\right\} \\ $$$$\Rightarrow\left(\mathrm{x},\mathrm{y},\mathrm{z},\mathrm{w}\right)\in\left\{\left(\frac{\mathrm{5}}{\mathrm{2}},\mathrm{4},\mathrm{6},\mathrm{2}\right),\left(\frac{−\mathrm{1}}{\mathrm{3}},−\mathrm{30},\mathrm{6},\mathrm{2}\right)\right\} \\ $$$$\bullet\mathrm{a}=\mathrm{xyz}=−\mathrm{2},\mathrm{b}=\mathrm{w}=−\mathrm{60},\mathrm{c}=\mathrm{xy}=\mathrm{12},\mathrm{d}=\mathrm{wz}=\mathrm{10} \\ $$$$\Rightarrow\mathrm{z}=\frac{−\mathrm{1}}{\mathrm{6}},\mathrm{wxz}−\mathrm{y}=\mathrm{26}\Leftrightarrow\mathrm{10x}−\mathrm{y}=\mathrm{12} \\ $$$$\mathrm{x}\left(\mathrm{10x}−\mathrm{26}\right)=\mathrm{12}\Leftrightarrow\mathrm{5x}^{\mathrm{2}} −\mathrm{13x}−\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}\in\left\{\mathrm{3},−\mathrm{2}/\mathrm{5}\right\}\Rightarrow\mathrm{y}\in\left\{\mathrm{4},−\mathrm{30}\right\} \\ $$$$\Rightarrow\left(\mathrm{x},\mathrm{y},\mathrm{z},\mathrm{w}\right)\in\left\{\left(\mathrm{3},\mathrm{4},\frac{−\mathrm{1}}{\mathrm{6}},−\mathrm{60}\right),\left(\frac{−\mathrm{2}}{\mathrm{5}},−\mathrm{30},\frac{−\mathrm{1}}{\mathrm{6}};−\mathrm{60}\right)\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *