Question Number 110467 by ajfour last updated on 29/Aug/20

Commented by ajfour last updated on 29/Aug/20

$${Find}\:{maximum}\:{F}\:{such}\:{that}\:{the} \\ $$$${cylinder}\:{resting}\:{against}\:{the}\:{ground} \\ $$$${and}\:{wall},\:{neither}\:{turns}\:{nor}\:{it}\:{moves}. \\ $$
Answered by mr W last updated on 29/Aug/20

Commented by mr W last updated on 29/Aug/20
![f_1 =μN_1 N_2 =f_1 =μN_1 f_2 =μN_2 =μ^2 N_1 F−Mg+N_1 +f_2 =0 F−Mg+(1+μ^2 )N_1 =0 ...(i) FR=(f_1 +f_2 )R F=μ(1+μ)N_1 ...(ii) F[1+((1+μ^2 )/(μ(1+μ)))]=Mg ⇒F=((μ(1+μ))/(2μ^2 +μ+1))Mg](https://www.tinkutara.com/question/Q110476.png)
$${f}_{\mathrm{1}} =\mu{N}_{\mathrm{1}} \\ $$$${N}_{\mathrm{2}} ={f}_{\mathrm{1}} =\mu{N}_{\mathrm{1}} \\ $$$${f}_{\mathrm{2}} =\mu{N}_{\mathrm{2}} =\mu^{\mathrm{2}} {N}_{\mathrm{1}} \\ $$$${F}−{Mg}+{N}_{\mathrm{1}} +{f}_{\mathrm{2}} =\mathrm{0} \\ $$$${F}−{Mg}+\left(\mathrm{1}+\mu^{\mathrm{2}} \right){N}_{\mathrm{1}} =\mathrm{0}\:\:\:…\left({i}\right) \\ $$$${FR}=\left({f}_{\mathrm{1}} +{f}_{\mathrm{2}} \right){R} \\ $$$${F}=\mu\left(\mathrm{1}+\mu\right){N}_{\mathrm{1}} \:\:\:…\left({ii}\right) \\ $$$${F}\left[\mathrm{1}+\frac{\mathrm{1}+\mu^{\mathrm{2}} }{\mu\left(\mathrm{1}+\mu\right)}\right]={Mg} \\ $$$$\Rightarrow{F}=\frac{\mu\left(\mathrm{1}+\mu\right)}{\mathrm{2}\mu^{\mathrm{2}} +\mu+\mathrm{1}}{Mg} \\ $$
Commented by ajfour last updated on 29/Aug/20
$${Correct}\:{and}\:{Nice}\:{Sir},\:{thanks}! \\ $$
Answered by mr W last updated on 29/Aug/20

Commented by mr W last updated on 29/Aug/20
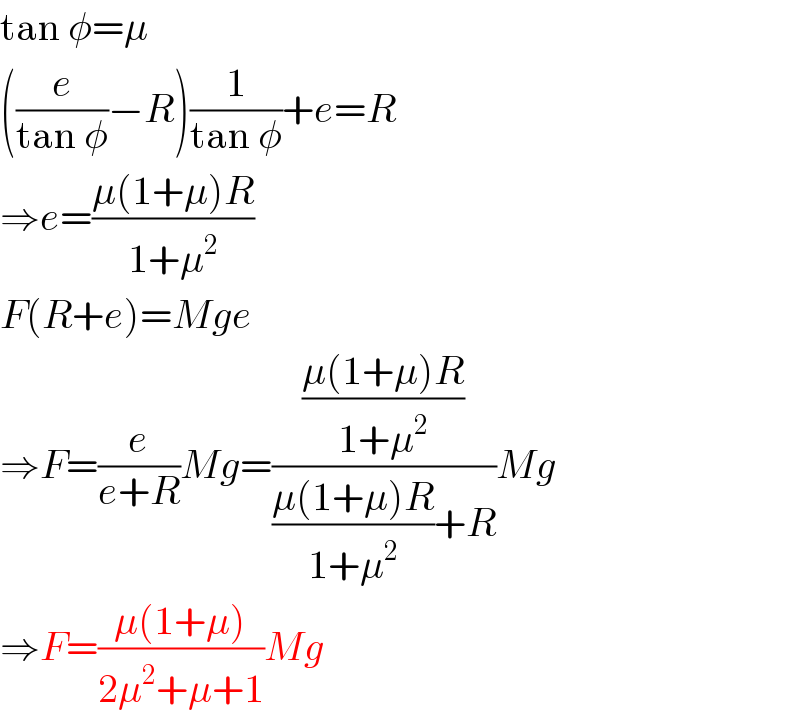
$$\mathrm{tan}\:\phi=\mu \\ $$$$\left(\frac{{e}}{\mathrm{tan}\:\phi}−{R}\right)\frac{\mathrm{1}}{\mathrm{tan}\:\phi}+{e}={R} \\ $$$$\Rightarrow{e}=\frac{\mu\left(\mathrm{1}+\mu\right){R}}{\mathrm{1}+\mu^{\mathrm{2}} } \\ $$$${F}\left({R}+{e}\right)={Mge} \\ $$$$\Rightarrow{F}=\frac{{e}}{{e}+{R}}{Mg}=\frac{\frac{\mu\left(\mathrm{1}+\mu\right){R}}{\mathrm{1}+\mu^{\mathrm{2}} }}{\frac{\mu\left(\mathrm{1}+\mu\right){R}}{\mathrm{1}+\mu^{\mathrm{2}} }+{R}}{Mg} \\ $$$$\Rightarrow{F}=\frac{\mu\left(\mathrm{1}+\mu\right)}{\mathrm{2}\mu^{\mathrm{2}} +\mu+\mathrm{1}}{Mg} \\ $$
Commented by ajfour last updated on 29/Aug/20

$$\mathcal{A}{wesome}!\:{Sir}. \\ $$
