Question Number 110503 by mohammad17 last updated on 29/Aug/20

Commented by Rio Michael last updated on 29/Aug/20
$${sorry}\:{sir}.\:{your}\:{answer}\:{wrong}.\:{check}\:{againt} \\ $$$$\mathrm{thank}\:\mathrm{you}. \\ $$$$\mathrm{thats}\:\mathrm{great}. \\ $$
Commented by bobhans last updated on 29/Aug/20
![(5a)method (1) Area= ∫_0 ^4 y^2 dy = [(1/3)y^3 ]_0 ^4 = ((64)/3) method (2) Area = ∫_0 ^(16) (4−(√x)) dx = [ 4x−(2/3)x(√x) ]_0 ^(16) = [ 64−((32.4)/3) ] = 64(1−(2/3)) = ((64)/3)](https://www.tinkutara.com/question/Q110512.png)
$$\left(\mathrm{5}{a}\right){method}\:\left(\mathrm{1}\right)\:{Area}=\:\underset{\mathrm{0}} {\overset{\mathrm{4}} {\int}}{y}^{\mathrm{2}} \:{dy}\:=\:\left[\frac{\mathrm{1}}{\mathrm{3}}{y}^{\mathrm{3}} \:\right]_{\mathrm{0}} ^{\mathrm{4}} =\:\frac{\mathrm{64}}{\mathrm{3}} \\ $$$${method}\:\left(\mathrm{2}\right)\:{Area}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{16}} {\int}}\left(\mathrm{4}−\sqrt{{x}}\right)\:{dx} \\ $$$$\:\:\:\:\:=\:\left[\:\mathrm{4}{x}−\frac{\mathrm{2}}{\mathrm{3}}{x}\sqrt{{x}}\:\right]_{\mathrm{0}} ^{\mathrm{16}} \\ $$$$\:\:\:\:\:=\:\left[\:\mathrm{64}−\frac{\mathrm{32}.\mathrm{4}}{\mathrm{3}}\:\right]\:=\:\mathrm{64}\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}\right)\:=\:\frac{\mathrm{64}}{\mathrm{3}} \\ $$
Commented by bobhans last updated on 29/Aug/20
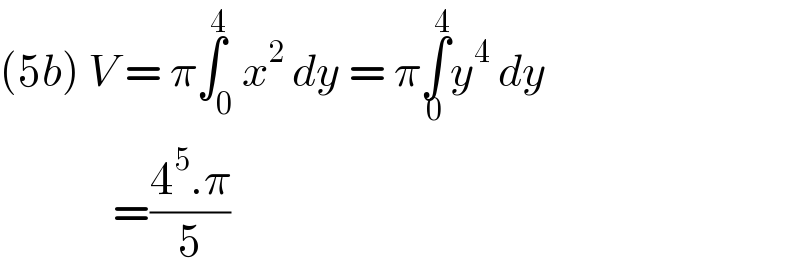
$$\left(\mathrm{5}{b}\right)\:{V}\:=\:\pi\overset{\mathrm{4}} {\int}_{\mathrm{0}} {x}^{\mathrm{2}} \:{dy}\:=\:\pi\underset{\mathrm{0}} {\overset{\mathrm{4}} {\int}}{y}^{\mathrm{4}} \:{dy}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{4}^{\mathrm{5}} .\pi}{\mathrm{5}} \\ $$
Commented by mohammad17 last updated on 29/Aug/20

$${sir}\:{are}\:{you}\:{sure}? \\ $$
Commented by mohammad17 last updated on 29/Aug/20

$${how}\:{x}^{\mathrm{2}} \\ $$
Commented by bemath last updated on 29/Aug/20

Commented by bemath last updated on 29/Aug/20
$$\mathrm{sir}.\:\mathrm{look}\:\mathrm{at}\:\mathrm{graph}.\:\mathrm{mr}\:\mathrm{bobhans}\:\mathrm{right} \\ $$
Answered by Rio Michael last updated on 29/Aug/20
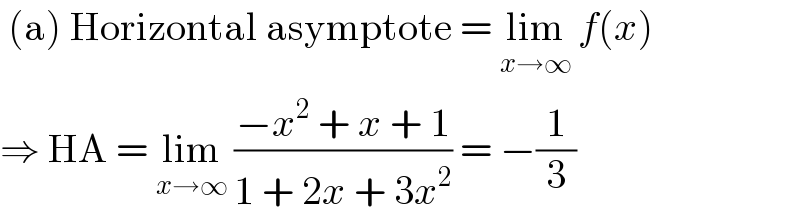
$$\:\left(\mathrm{a}\right)\:\mathrm{Horizontal}\:\mathrm{asymptote}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{f}\left({x}\right) \\ $$$$\Rightarrow\:\mathrm{HA}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{−{x}^{\mathrm{2}} \:+\:{x}\:+\:\mathrm{1}}{\mathrm{1}\:+\:\mathrm{2}{x}\:+\:\mathrm{3}{x}^{\mathrm{2}} }\:=\:−\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by mohammad17 last updated on 29/Aug/20

$${thank}\:{you}\:{sir} \\ $$
Answered by Rio Michael last updated on 29/Aug/20
![x: −1 −0.5 0 0.5 1 y : 3 2.25 2 2.25 3 where y = 2 + x^2 and we define h = 0.5 by the tripezoidal rule ∫_a ^b y dx = (h/2) [ y_0 + y_4 + 2(y_1 + y_2 + y_3 )] ⇒ ∫_(−1) ^( 1) (2+ x^2 ) dx ≈ ((0.5)/2) [ 3 + 3 + 2(2.25 + 2 + 2.25)] = 4.75 Checking: ∫_(−1) ^1 (2 + x^2 ) dx = [2x + (x^3 /3)]_(−1) ^1 = 2.33 −(−2.33) = 4.66](https://www.tinkutara.com/question/Q110511.png)
$$\:\:{x}:\:\:\:\:\:−\mathrm{1}\:\:\:\:\:−\mathrm{0}.\mathrm{5}\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{0}.\mathrm{5}\:\:\:\:\:\:\mathrm{1} \\ $$$$\:{y}\::\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}.\mathrm{25}\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{2}.\mathrm{25}\:\:\:\:\:\mathrm{3} \\ $$$$\:\mathrm{where}\:{y}\:=\:\mathrm{2}\:+\:{x}^{\mathrm{2}} \:\:\mathrm{and}\:\mathrm{we}\:\mathrm{define}\:{h}\:=\:\mathrm{0}.\mathrm{5} \\ $$$$\mathrm{by}\:\mathrm{the}\:\mathrm{tripezoidal}\:\mathrm{rule} \\ $$$$\int_{{a}} ^{{b}} {y}\:{dx}\:=\:\frac{{h}}{\mathrm{2}}\:\left[\:{y}_{\mathrm{0}} \:+\:{y}_{\mathrm{4}} \:+\:\mathrm{2}\left({y}_{\mathrm{1}} \:+\:{y}_{\mathrm{2}} \:+\:{y}_{\mathrm{3}} \right)\right] \\ $$$$\Rightarrow\:\int_{−\mathrm{1}} ^{\:\mathrm{1}} \left(\mathrm{2}+\:{x}^{\mathrm{2}} \right)\:{dx}\:\approx\:\frac{\mathrm{0}.\mathrm{5}}{\mathrm{2}}\:\left[\:\mathrm{3}\:+\:\mathrm{3}\:+\:\mathrm{2}\left(\mathrm{2}.\mathrm{25}\:+\:\mathrm{2}\:+\:\mathrm{2}.\mathrm{25}\right)\right]\:=\:\mathrm{4}.\mathrm{75} \\ $$$$\:\mathrm{Checking}:\:\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:\left(\mathrm{2}\:+\:{x}^{\mathrm{2}} \right)\:{dx}\:=\:\left[\mathrm{2}{x}\:+\:\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right]_{−\mathrm{1}} ^{\mathrm{1}} \:=\:\mathrm{2}.\mathrm{33}\:−\left(−\mathrm{2}.\mathrm{33}\right)\:=\:\mathrm{4}.\mathrm{66} \\ $$
Answered by Rio Michael last updated on 29/Aug/20
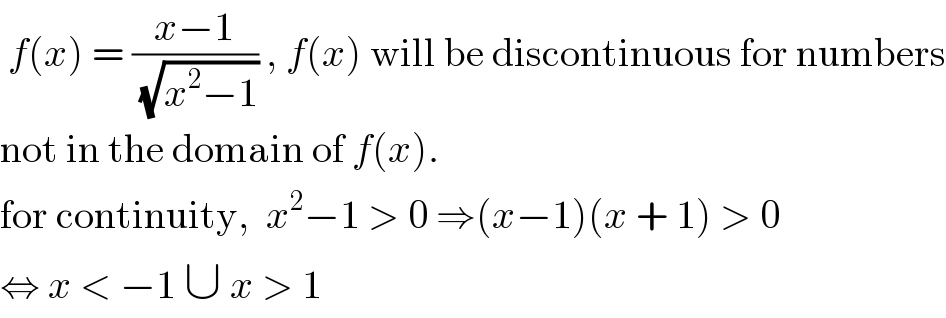
$$\:{f}\left({x}\right)\:=\:\frac{{x}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:,\:{f}\left({x}\right)\:\mathrm{will}\:\mathrm{be}\:\mathrm{discontinuous}\:\mathrm{for}\:\mathrm{numbers} \\ $$$$\mathrm{not}\:\mathrm{in}\:\mathrm{the}\:\mathrm{domain}\:\mathrm{of}\:{f}\left({x}\right). \\ $$$$\mathrm{for}\:\mathrm{continuity},\:\:{x}^{\mathrm{2}} −\mathrm{1}\:>\:\mathrm{0}\:\Rightarrow\left({x}−\mathrm{1}\right)\left({x}\:+\:\mathrm{1}\right)\:>\:\mathrm{0} \\ $$$$\Leftrightarrow\:{x}\:<\:−\mathrm{1}\:\cup\:{x}\:>\:\mathrm{1}\: \\ $$
Answered by Aziztisffola last updated on 29/Aug/20
![(a) y=−(1/(3 )) (lim_(x→∞) f(x)=−(1/3)) (b) D_f =]−∞;−1[∪]1;+∞[ (c) Riemann sum use △x=(2/5)](https://www.tinkutara.com/question/Q110544.png)
$$\:\left(\mathrm{a}\right)\:\mathrm{y}=−\frac{\mathrm{1}}{\mathrm{3}\:}\:\:\left(\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{f}\left(\mathrm{x}\right)=−\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\left.\:\left(\mathrm{b}\right)\:\mathrm{D}_{\mathrm{f}} =\right]−\infty;−\mathrm{1}\left[\cup\right]\mathrm{1};+\infty\left[\right. \\ $$$$\:\left(\mathrm{c}\right)\:\mathrm{Riemann}\:\mathrm{sum}\:\mathrm{use}\:\bigtriangleup\mathrm{x}=\frac{\mathrm{2}}{\mathrm{5}} \\ $$
