Question Number 110545 by peter frank last updated on 29/Aug/20
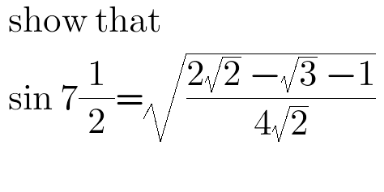
Commented by Dwaipayan Shikari last updated on 29/Aug/20

$$\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}−\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}} \\ $$
Commented by Dwaipayan Shikari last updated on 29/Aug/20

$$\frac{{e}^{\frac{\pi{i}}{\mathrm{24}}} −{e}^{\frac{−\pi{i}}{\mathrm{24}}} }{\mathrm{2}{i}} \\ $$
Answered by Dwaipayan Shikari last updated on 29/Aug/20
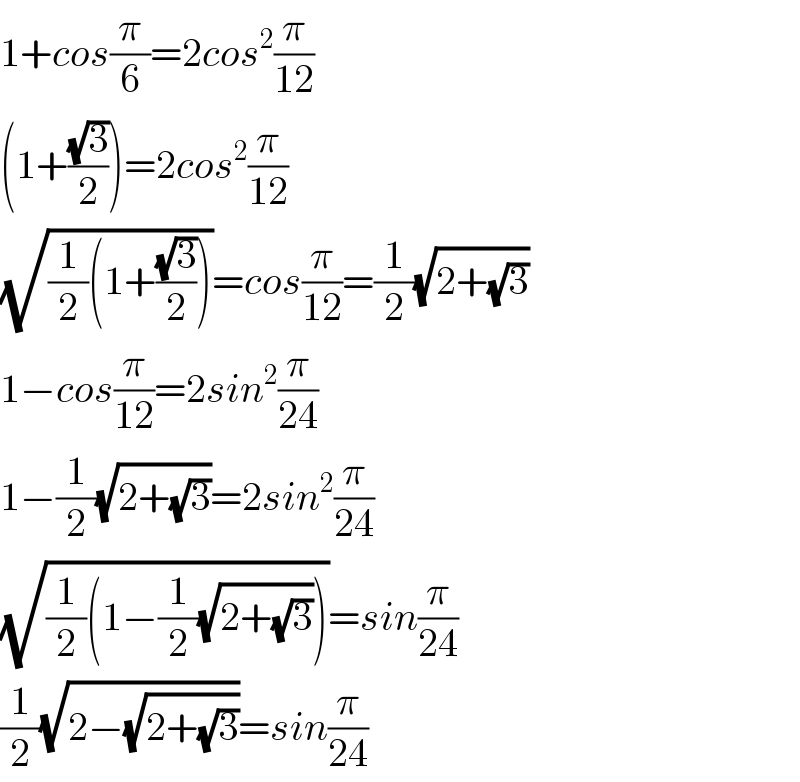
$$\mathrm{1}+{cos}\frac{\pi}{\mathrm{6}}=\mathrm{2}{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{12}} \\ $$$$\left(\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\mathrm{2}{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{12}} \\ $$$$\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}={cos}\frac{\pi}{\mathrm{12}}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$$\mathrm{1}−{cos}\frac{\pi}{\mathrm{12}}=\mathrm{2}{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{24}} \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}=\mathrm{2}{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{24}} \\ $$$$\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right)}={sin}\frac{\pi}{\mathrm{24}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}−\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}}={sin}\frac{\pi}{\mathrm{24}} \\ $$
Commented by peter frank last updated on 29/Aug/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
