Question Number 110549 by shahria14 last updated on 29/Aug/20
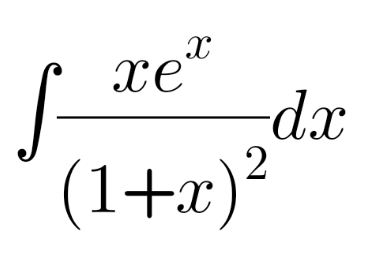
Commented by peter frank last updated on 29/Aug/20
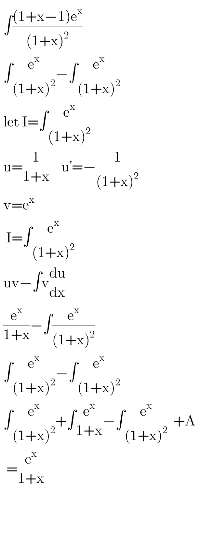
Answered by peter frank last updated on 29/Aug/20

$$\mathrm{an}\overset{} {\mathrm{s}}\:=\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{x}} \\ $$
Answered by Dwaipayan Shikari last updated on 29/Aug/20
$$\int\frac{{xe}^{{x}} +{e}^{{x}} }{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }−\frac{{e}^{{x}} }{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{dx} \\ $$$$\int{e}^{{x}} \left(\frac{\mathrm{1}}{\mathrm{1}+{x}}−\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }\right){dx}=\frac{{e}^{{x}} }{\mathrm{1}+{x}}+{C} \\ $$
