Question Number 110614 by mathdave last updated on 29/Aug/20

Answered by Dwaipayan Shikari last updated on 29/Aug/20
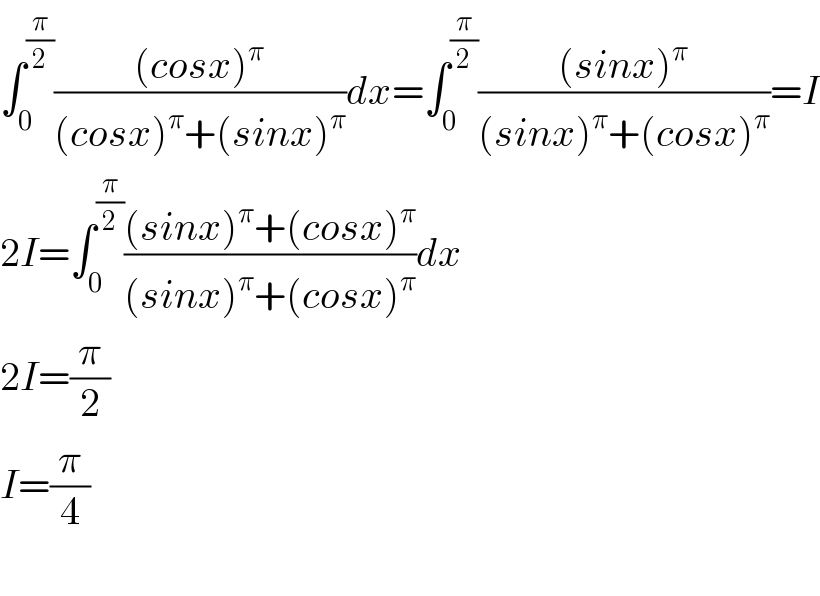
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left({cosx}\right)^{\pi} }{\left({cosx}\right)^{\pi} +\left({sinx}\right)^{\pi} }{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left({sinx}\right)^{\pi} }{\left({sinx}\right)^{\pi} +\left({cosx}\right)^{\pi} }={I} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left({sinx}\right)^{\pi} +\left({cosx}\right)^{\pi} }{\left({sinx}\right)^{\pi} +\left({cosx}\right)^{\pi} }{dx} \\ $$$$\mathrm{2}{I}=\frac{\pi}{\mathrm{2}} \\ $$$${I}=\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 29/Aug/20

$${perfect}\:… \\ $$
