Question Number 110620 by peter frank last updated on 29/Aug/20

Answered by Dwaipayan Shikari last updated on 29/Aug/20
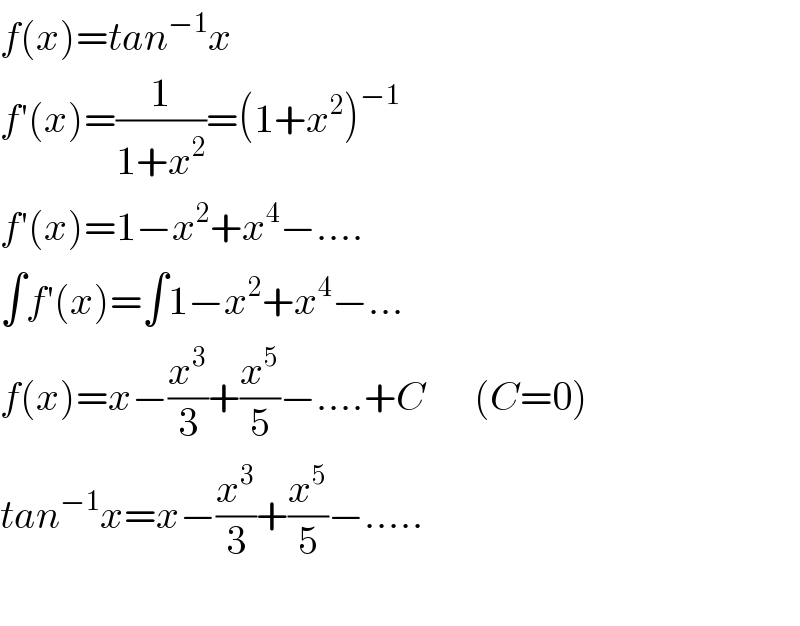
$${f}\left({x}\right)={tan}^{−\mathrm{1}} {x} \\ $$$${f}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }=\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{−\mathrm{1}} \\ $$$${f}'\left({x}\right)=\mathrm{1}−{x}^{\mathrm{2}} +{x}^{\mathrm{4}} −…. \\ $$$$\int{f}'\left({x}\right)=\int\mathrm{1}−{x}^{\mathrm{2}} +{x}^{\mathrm{4}} −… \\ $$$${f}\left({x}\right)={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}−….+{C}\:\:\:\:\:\:\left({C}=\mathrm{0}\right) \\ $$$${tan}^{−\mathrm{1}} {x}={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}−….. \\ $$$$ \\ $$
Commented by peter frank last updated on 30/Aug/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
