Question Number 110848 by ajfour last updated on 31/Aug/20
Commented by ajfour last updated on 31/Aug/20
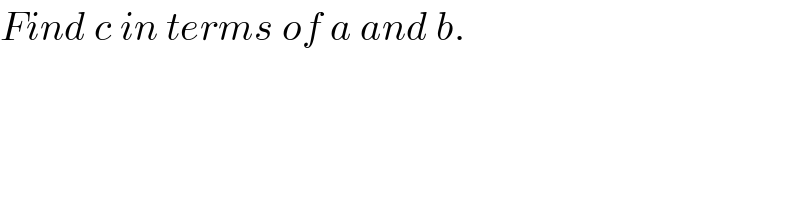
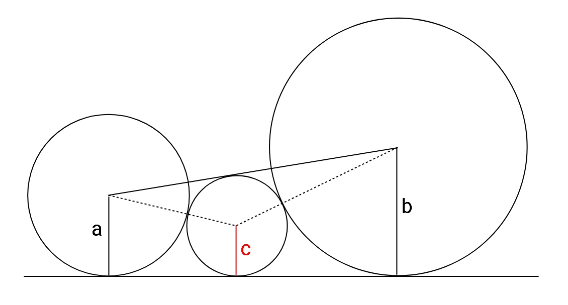
$${Find}\:{c}\:{in}\:{terms}\:{of}\:{a}\:{and}\:{b}. \\ $$
Commented by bemath last updated on 31/Aug/20
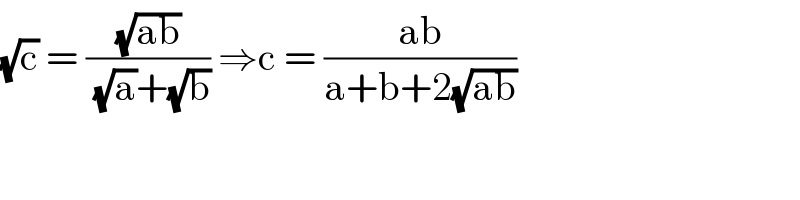
$$\sqrt{\mathrm{c}}\:=\:\frac{\sqrt{\mathrm{ab}}}{\:\sqrt{\mathrm{a}}+\sqrt{\mathrm{b}}}\:\Rightarrow\mathrm{c}\:=\:\frac{\mathrm{ab}}{\mathrm{a}+\mathrm{b}+\mathrm{2}\sqrt{\mathrm{ab}}} \\ $$
Commented by mr W last updated on 31/Aug/20
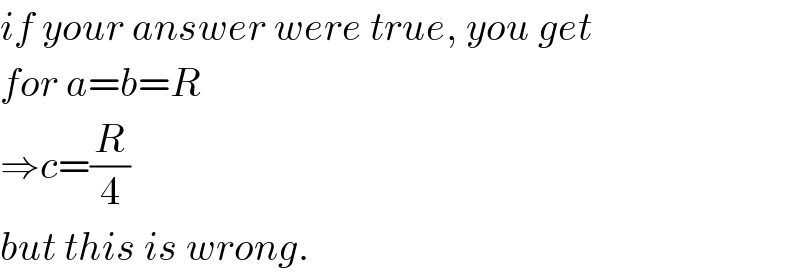
$${if}\:{your}\:{answer}\:{were}\:{true},\:{you}\:{get} \\ $$$${for}\:{a}={b}={R} \\ $$$$\Rightarrow{c}=\frac{{R}}{\mathrm{4}} \\ $$$${but}\:{this}\:{is}\:{wrong}. \\ $$
Answered by mr W last updated on 31/Aug/20
![[(√((a+c)^2 −(a−c)^2 ))+(√((b+c)^2 −(b−c)^2 ))]^2 +(b−a)^2 =[(√((a+c)^2 −c^2 ))+(√((b+c)^2 −c^2 ))]^2 [2(√(ac))+2(√(bc))]^2 +(b−a)^2 =[(√(a(a+2c)))+(√(b(b+2c)))]^2 (a+b+4(√(ab)))c−ab=(√(ab(a+2c)(b+2c))) (a+b+4(√(ab)))^2 c^2 +a^2 b^2 −2ab(a+b+4(√(ab)))c=ab[ab+2(a+b)c+4c^2 ] [a^2 +b^2 +14ab+8(a+b)(√(ab))]c=4ab(a+b+2(√(ab))) ⇒c=((4ab(a+b+2(√(ab))))/(a^2 +b^2 +14ab+8(a+b)(√(ab)))) ⇒c=((4ab)/(a+b+6(√(ab)))) if b=a: ⇒c=(a/2) ⇒ok](https://www.tinkutara.com/question/Q110850.png)
$$\left[\sqrt{\left({a}+{c}\right)^{\mathrm{2}} −\left({a}−{c}\right)^{\mathrm{2}} }+\sqrt{\left({b}+{c}\right)^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} }\right]^{\mathrm{2}} +\left({b}−{a}\right)^{\mathrm{2}} =\left[\sqrt{\left({a}+{c}\right)^{\mathrm{2}} −{c}^{\mathrm{2}} }+\sqrt{\left({b}+{c}\right)^{\mathrm{2}} −{c}^{\mathrm{2}} }\right]^{\mathrm{2}} \\ $$$$\left[\mathrm{2}\sqrt{{ac}}+\mathrm{2}\sqrt{{bc}}\right]^{\mathrm{2}} +\left({b}−{a}\right)^{\mathrm{2}} =\left[\sqrt{{a}\left({a}+\mathrm{2}{c}\right)}+\sqrt{{b}\left({b}+\mathrm{2}{c}\right)}\right]^{\mathrm{2}} \\ $$$$\left({a}+{b}+\mathrm{4}\sqrt{{ab}}\right){c}−{ab}=\sqrt{{ab}\left({a}+\mathrm{2}{c}\right)\left({b}+\mathrm{2}{c}\right)} \\ $$$$\left({a}+{b}+\mathrm{4}\sqrt{{ab}}\right)^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{2}{ab}\left({a}+{b}+\mathrm{4}\sqrt{{ab}}\right){c}={ab}\left[{ab}+\mathrm{2}\left({a}+{b}\right){c}+\mathrm{4}{c}^{\mathrm{2}} \right] \\ $$$$\left[{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{14}{ab}+\mathrm{8}\left({a}+{b}\right)\sqrt{{ab}}\right]{c}=\mathrm{4}{ab}\left({a}+{b}+\mathrm{2}\sqrt{{ab}}\right) \\ $$$$\Rightarrow{c}=\frac{\mathrm{4}{ab}\left({a}+{b}+\mathrm{2}\sqrt{{ab}}\right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{14}{ab}+\mathrm{8}\left({a}+{b}\right)\sqrt{{ab}}} \\ $$$$\Rightarrow{c}=\frac{\mathrm{4}{ab}}{{a}+{b}+\mathrm{6}\sqrt{{ab}}} \\ $$$${if}\:{b}={a}: \\ $$$$\Rightarrow{c}=\frac{{a}}{\mathrm{2}}\:\Rightarrow{ok} \\ $$
Commented by ajfour last updated on 31/Aug/20
$${followed}\:{sir}!\:\:\mathrm{2}\:{good}!\:{thanks}. \\ $$
Answered by mnjuly1970 last updated on 31/Aug/20

$${common}\:{tangant},\:{circles}\:\mathrm{1}\:{and}\:\mathrm{2}\:\:\::=\mathrm{2}\sqrt{{ca}} \\ $$$$ \\ $$$${common}\:{tangant},{circles}\:\mathrm{2}\:{and}\:\mathrm{3}\:\:\:\::=\mathrm{2}\sqrt{{cb}}\: \\ $$$$ \\ $$$${common}\:{tangant},{circles}\:\mathrm{1}\:{and}\:\mathrm{3}\:\::\:=\:\mathrm{2}\sqrt{{ab}} \\ $$$$ \\ $$$$\mathrm{2}\sqrt{{ab}}\:=\mathrm{2}\sqrt{{ac}}\:+\mathrm{2}\sqrt{{bc}\:}\:\Rightarrow\frac{\sqrt{{ab}}}{\:\sqrt{{abc}}}=\frac{\sqrt{{ac}}}{\:\sqrt{{abc}}}\:+\frac{\sqrt{{bc}}}{\:\sqrt{{abc}}} \\ $$$$\:\:\:\therefore\:\frac{\mathrm{1}}{\:\sqrt{{c}}}=\frac{\mathrm{1}}{\:\sqrt{{a}}}+\frac{\mathrm{1}}{\:\sqrt{{b}}}\:\:….\left({q}.{e}.{d}\right) \\ $$$$\:\:\:\:\:\:\:\:\:….\mathscr{M}.\mathscr{N}.{july}\:\mathrm{1970}\:# \\ $$$$ \\ $$
Answered by ajfour last updated on 31/Aug/20

$${let}\:{center}\:{of}\:{middle}\:{circle}\:\:{C}\left(\mathrm{0},{c}\right) \\ $$$${left}\:{circle}\:\:{A}\left(−\mathrm{2}\sqrt{{ac}},\:{a}\right) \\ $$$${right}\:{circle}\:\:{B}\left(\mathrm{2}\sqrt{{bc}},\:{b}\right) \\ $$$${eq}.\:{of}\:{AB}:\:\:\:{y}−{a}=\frac{\left(\sqrt{{b}}−\sqrt{{a}}\right)}{\mathrm{2}\sqrt{{c}}}\left({x}+\mathrm{2}\sqrt{{ac}}\right) \\ $$$${its}\:\bot{distance}\:{from}\:{C}\:{is}\:{c}. \\ $$$$\Rightarrow\:\:\:{c}=\frac{\left(\sqrt{{b}}−\sqrt{{a}}\right)\sqrt{{a}}+{a}−{c}}{\:\sqrt{\mathrm{1}+\frac{\left(\sqrt{{b}}−\sqrt{{a}}\right)^{\mathrm{2}} }{\mathrm{4}{c}}}} \\ $$$$\:\:\:{c}\sqrt{\mathrm{1}+\frac{\left(\sqrt{{b}}−\sqrt{{a}}\right)^{\mathrm{2}} }{\mathrm{4}{c}}}=\sqrt{{ab}}−{c} \\ $$$$\Rightarrow\:\:\:{c}^{\mathrm{2}} +\frac{\left({b}+{a}−\mathrm{2}\sqrt{{ab}}\right){c}}{\mathrm{4}}={ab}+{c}^{\mathrm{2}} −\mathrm{2}{c}\sqrt{{ab}} \\ $$$$\Rightarrow\:\:{c}=\frac{{ab}}{\mathrm{2}\sqrt{{ab}}+\frac{{b}+{a}−\mathrm{2}\sqrt{{ab}}}{\mathrm{4}}} \\ $$$$\:\:\:\:\:{c}=\frac{\mathrm{4}{ab}}{{a}+{b}+\mathrm{6}\sqrt{{ab}}}\:. \\ $$
