Question Number 110861 by apriani last updated on 31/Aug/20

Answered by bemath last updated on 31/Aug/20
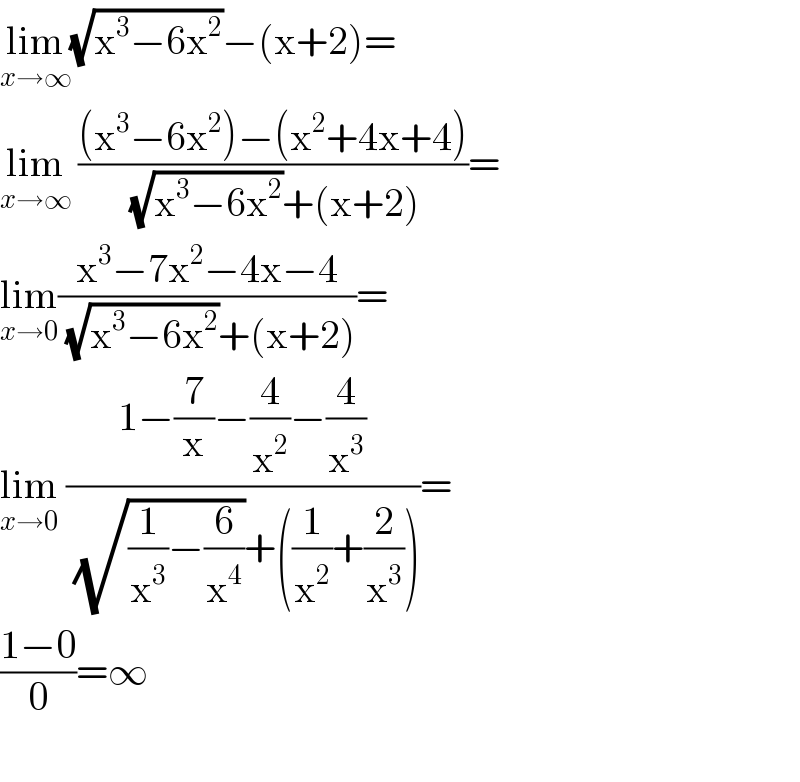
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt{\mathrm{x}^{\mathrm{3}} −\mathrm{6x}^{\mathrm{2}} }−\left(\mathrm{x}+\mathrm{2}\right)= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left(\mathrm{x}^{\mathrm{3}} −\mathrm{6x}^{\mathrm{2}} \right)−\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{4}\right)}{\:\sqrt{\mathrm{x}^{\mathrm{3}} −\mathrm{6x}^{\mathrm{2}} }+\left(\mathrm{x}+\mathrm{2}\right)}= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{7x}^{\mathrm{2}} −\mathrm{4x}−\mathrm{4}}{\:\sqrt{\mathrm{x}^{\mathrm{3}} −\mathrm{6x}^{\mathrm{2}} }+\left(\mathrm{x}+\mathrm{2}\right)}= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\frac{\mathrm{7}}{\mathrm{x}}−\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{3}} }}{\:\sqrt{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }−\frac{\mathrm{6}}{\mathrm{x}^{\mathrm{4}} }}+\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{3}} }\right)}= \\ $$$$\frac{\mathrm{1}−\mathrm{0}}{\mathrm{0}}=\infty \\ $$$$ \\ $$
Answered by Aziztisffola last updated on 31/Aug/20
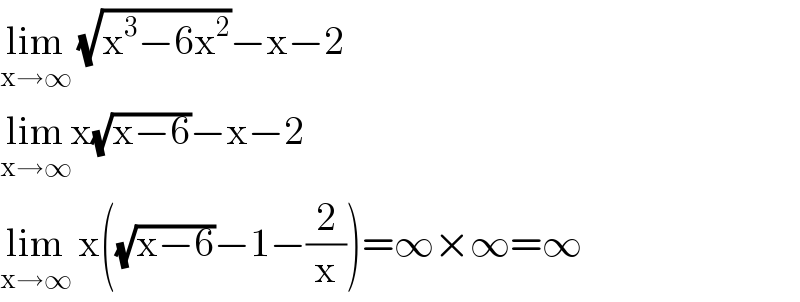
$$\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{x}^{\mathrm{3}} −\mathrm{6x}^{\mathrm{2}} }−\mathrm{x}−\mathrm{2} \\ $$$$\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}x}\sqrt{\mathrm{x}−\mathrm{6}}−\mathrm{x}−\mathrm{2} \\ $$$$\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{x}\left(\sqrt{\mathrm{x}−\mathrm{6}}−\mathrm{1}−\frac{\mathrm{2}}{\mathrm{x}}\right)=\infty×\infty=\infty \\ $$
