Question Number 110869 by Study last updated on 31/Aug/20

Answered by mathdave last updated on 31/Aug/20
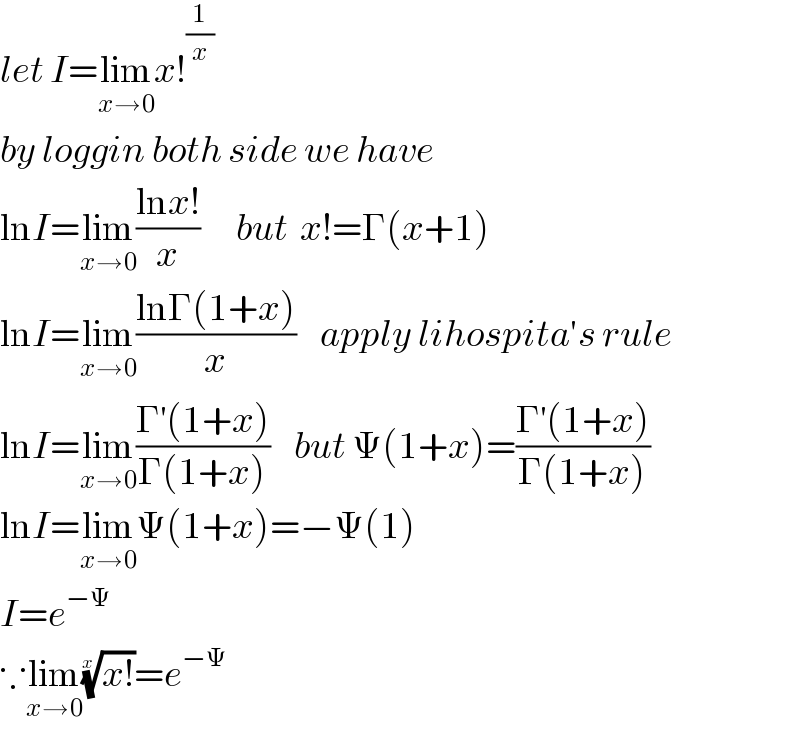
$${let}\:{I}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{x}!^{\frac{\mathrm{1}}{{x}}} \\ $$$${by}\:{loggin}\:{both}\:{side}\:{we}\:{have} \\ $$$$\mathrm{ln}{I}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}{x}!}{{x}}\:\:\:\:\:\:{but}\:\:{x}!=\Gamma\left({x}+\mathrm{1}\right) \\ $$$$\mathrm{ln}{I}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\Gamma\left(\mathrm{1}+{x}\right)}{{x}}\:\:\:\:{apply}\:{lihospita}'{s}\:{rule} \\ $$$$\mathrm{ln}{I}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\Gamma^{'} \left(\mathrm{1}+{x}\right)}{\Gamma\left(\mathrm{1}+{x}\right)}\:\:\:\:{but}\:\Psi\left(\mathrm{1}+{x}\right)=\frac{\Gamma^{'} \left(\mathrm{1}+{x}\right)}{\Gamma\left(\mathrm{1}+{x}\right)} \\ $$$$\mathrm{ln}{I}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\Psi\left(\mathrm{1}+{x}\right)=−\Psi\left(\mathrm{1}\right) \\ $$$${I}={e}^{−\Psi} \\ $$$$\because\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\sqrt[{{x}}]{{x}!}={e}^{−\Psi} \:\:\:\: \\ $$
