Question Number 110920 by Dwaipayan Shikari last updated on 31/Aug/20

Commented by Dwaipayan Shikari last updated on 31/Aug/20
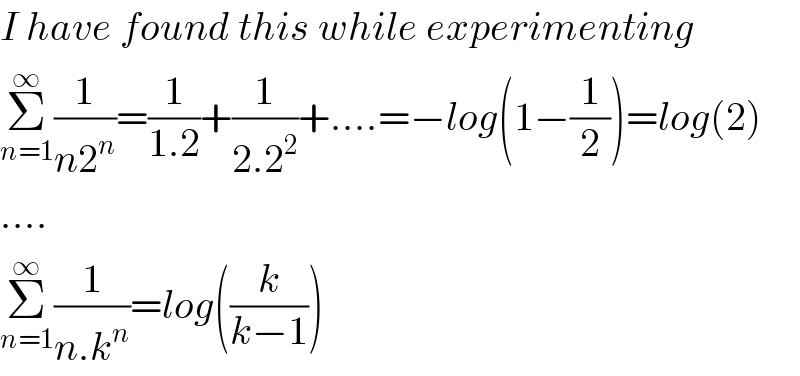
$${I}\:{have}\:{found}\:{this}\:{while}\:{experimenting} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\mathrm{2}^{{n}} }=\frac{\mathrm{1}}{\mathrm{1}.\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}.\mathrm{2}^{\mathrm{2}} }+….=−{log}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)={log}\left(\mathrm{2}\right) \\ $$$$…. \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}.{k}^{{n}} }={log}\left(\frac{{k}}{{k}−\mathrm{1}}\right) \\ $$
Answered by mathmax by abdo last updated on 01/Sep/20

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\:\:\mathrm{with}\:\:\mid\mathrm{x}\mid<\mathrm{1}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=−\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\:+\mathrm{c}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{c}=\mathrm{f}\left(\mathrm{0}\right)\:=\mathrm{0}\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\:=−\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\:\mathrm{let}\:\mathrm{change}\:\mathrm{x}\:\mathrm{by}\:\frac{\mathrm{1}}{\mathrm{x}}\:\:\mathrm{with}\:\mid\mathrm{x}\mid>\mathrm{1}\:\mathrm{we}\:\mathrm{get} \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{nx}^{\mathrm{n}} }\:=−\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}\right)=−\mathrm{ln}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)\:=\mathrm{ln}\left(\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}}\right) \\ $$$$\mathrm{for}\:\mathrm{x}=\mathrm{k}\:\:\mathrm{integr}\:\mathrm{we}\:\mathrm{get}\: \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{nk}^{\mathrm{n}} }\:=\mathrm{ln}\left(\frac{\mathrm{k}}{\mathrm{k}−\mathrm{1}}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 01/Sep/20

$${Thanking}\:{you} \\ $$
