Question Number 110951 by ZiYangLee last updated on 01/Sep/20
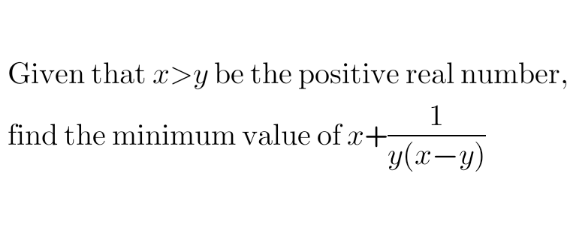
Answered by $@y@m last updated on 01/Sep/20
![Let y=kx (0<k<1) Let z=x+(1/(y(x−y))) ⇒ z=x+(1/(kx(x−kx))) ⇒z =x+(1/(k(1−k)x^2 )) .....(1) (dz/dx)=1−(2/(k(1−k)x^3 )) ....(2) For maxima or minima, (dz/dx)=0 1−(2/(k(1−k)x^3 )) =0 1=(2/(k(1−k)x^3 )) x^3 =(2/(k(1−k))) x={(2/(k(1−k)))}^(1/3) ...(3) (d^2 z/dx^2 )=(6/(k(1−k)x^4 )) (d^2 z/dx^2 )]_(at x={(2/(k(1−k)))}^(1/3) ) =(6/(k(1−k){(2/(k(1−k)))}^(4/3) )) =((6{k(1−k)}^(1/3) )/2^(4/3) )>0 (∵ 0<k<1) ∴ z is minimum when x={(2/(k(1−k)))}^(1/3) From (1), z =x+(1/(k(1−k)x^2 )) ⇒z=((k(1−k)x^3 +1)/(k(1−k)x^2 )) ⇒z_(min.) =((k(1−k)×(2/(k(1−k)))+1)/(k(1−k){(2/(k(1−k)))}^(2/3) )) ⇒z_(min.) =((3{k(1−k)}^(1/3) )/2^(2/3) ) ....(4) Now, let v=k(1−k) It can be shown that v is maximum when k=(1/2). v_(max.) =(1/4) From (4), it is evident that z is minimum when v is maximum. =3.((1/2))^(2/3) ((1/2))^(2/3) =3.((2/3))^(4/3)](https://www.tinkutara.com/question/Q110962.png)
$${Let}\:{y}={kx}\:\left(\mathrm{0}<{k}<\mathrm{1}\right) \\ $$$${Let}\:{z}={x}+\frac{\mathrm{1}}{{y}\left({x}−{y}\right)} \\ $$$$\Rightarrow\:{z}={x}+\frac{\mathrm{1}}{{kx}\left({x}−{kx}\right)} \\ $$$$\:\Rightarrow{z}\:={x}+\frac{\mathrm{1}}{{k}\left(\mathrm{1}−{k}\right){x}^{\mathrm{2}} }\:…..\left(\mathrm{1}\right) \\ $$$$\frac{{dz}}{{dx}}=\mathrm{1}−\frac{\mathrm{2}}{{k}\left(\mathrm{1}−{k}\right){x}^{\mathrm{3}} }\:….\left(\mathrm{2}\right) \\ $$$${For}\:{maxima}\:{or}\:{minima}, \\ $$$$\frac{{dz}}{{dx}}=\mathrm{0} \\ $$$$\mathrm{1}−\frac{\mathrm{2}}{{k}\left(\mathrm{1}−{k}\right){x}^{\mathrm{3}} }\:=\mathrm{0} \\ $$$$\mathrm{1}=\frac{\mathrm{2}}{{k}\left(\mathrm{1}−{k}\right){x}^{\mathrm{3}} }\: \\ $$$${x}^{\mathrm{3}} =\frac{\mathrm{2}}{{k}\left(\mathrm{1}−{k}\right)}\:\: \\ $$$${x}=\left\{\frac{\mathrm{2}}{{k}\left(\mathrm{1}−{k}\right)}\right\}^{\frac{\mathrm{1}}{\mathrm{3}}} …\left(\mathrm{3}\right)\:\: \\ $$$$\frac{{d}^{\mathrm{2}} {z}}{{dx}^{\mathrm{2}} }=\frac{\mathrm{6}}{{k}\left(\mathrm{1}−{k}\right){x}^{\mathrm{4}} } \\ $$$$\left.\frac{{d}^{\mathrm{2}} {z}}{{dx}^{\mathrm{2}} }\right]_{{at}\:{x}=\left\{\frac{\mathrm{2}}{{k}\left(\mathrm{1}−{k}\right)}\right\}^{\frac{\mathrm{1}}{\mathrm{3}}} } =\frac{\mathrm{6}}{{k}\left(\mathrm{1}−{k}\right)\left\{\frac{\mathrm{2}}{{k}\left(\mathrm{1}−{k}\right)}\right\}^{\frac{\mathrm{4}}{\mathrm{3}}} } \\ $$$$ \\ $$$$=\frac{\mathrm{6}\left\{{k}\left(\mathrm{1}−{k}\right)\right\}^{\frac{\mathrm{1}}{\mathrm{3}}} }{\mathrm{2}^{\frac{\mathrm{4}}{\mathrm{3}}} }>\mathrm{0}\:\left(\because\:\mathrm{0}<{k}<\mathrm{1}\right) \\ $$$$\therefore\:{z}\:{is}\:{minimum}\:{when}\:{x}=\left\{\frac{\mathrm{2}}{{k}\left(\mathrm{1}−{k}\right)}\right\}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${From}\:\left(\mathrm{1}\right), \\ $$$$\:{z}\:={x}+\frac{\mathrm{1}}{{k}\left(\mathrm{1}−{k}\right){x}^{\mathrm{2}} }\: \\ $$$$\Rightarrow{z}=\frac{{k}\left(\mathrm{1}−{k}\right){x}^{\mathrm{3}} +\mathrm{1}}{{k}\left(\mathrm{1}−{k}\right){x}^{\mathrm{2}} } \\ $$$$\Rightarrow{z}_{{min}.} =\frac{{k}\left(\mathrm{1}−{k}\right)×\frac{\mathrm{2}}{{k}\left(\mathrm{1}−{k}\right)}+\mathrm{1}}{{k}\left(\mathrm{1}−{k}\right)\left\{\frac{\mathrm{2}}{{k}\left(\mathrm{1}−{k}\right)}\right\}^{\frac{\mathrm{2}}{\mathrm{3}}} } \\ $$$$\Rightarrow{z}_{{min}.} =\frac{\mathrm{3}\left\{{k}\left(\mathrm{1}−{k}\right)\right\}^{\frac{\mathrm{1}}{\mathrm{3}}} }{\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:….\left(\mathrm{4}\right) \\ $$$${Now},\:{let}\:{v}={k}\left(\mathrm{1}−{k}\right) \\ $$$${It}\:{can}\:{be}\:{shown}\:{that}\:{v}\:{is}\:{maximum} \\ $$$${when}\:{k}=\frac{\mathrm{1}}{\mathrm{2}}. \\ $$$${v}_{{max}.} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${From}\:\left(\mathrm{4}\right),\:{it}\:{is}\:{evident}\:{that}\:{z}\:{is}\:{minimum}\:{when}\:{v}\:{is}\:{maximum}. \\ $$$$\:\:\:=\mathrm{3}.\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\:\:=\mathrm{3}.\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} \\ $$$$ \\ $$
Commented by ZiYangLee last updated on 01/Sep/20

$$\mathrm{Thanks}\:\mathrm{Bro}! \\ $$
Commented by $@y@m last updated on 01/Sep/20
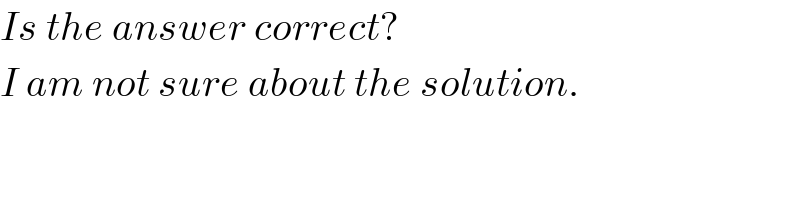
$${Is}\:{the}\:{answer}\:{correct}? \\ $$$${I}\:{am}\:{not}\:{sure}\:{about}\:{the}\:{solution}. \\ $$
Answered by 1549442205PVT last updated on 01/Sep/20
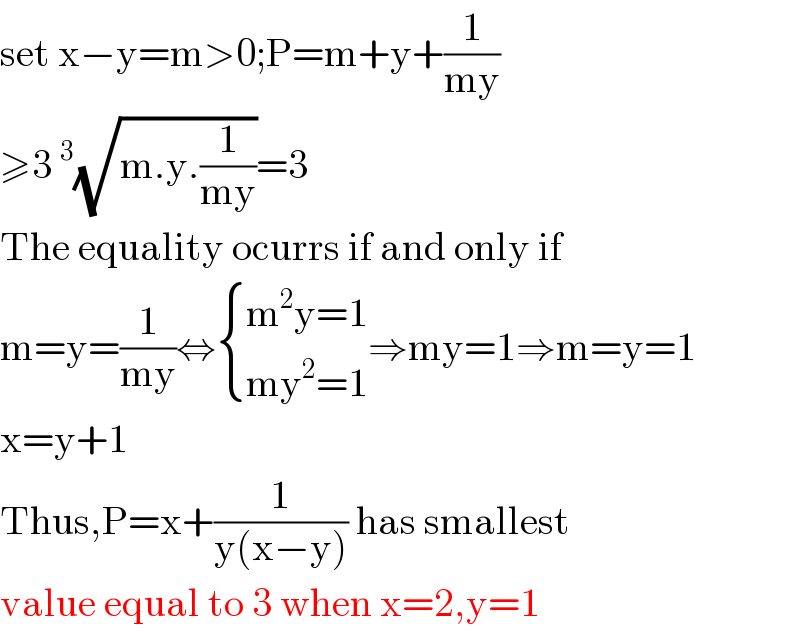
$$\mathrm{set}\:\mathrm{x}−\mathrm{y}=\mathrm{m}>\mathrm{0};\mathrm{P}=\mathrm{m}+\mathrm{y}+\frac{\mathrm{1}}{\mathrm{my}} \\ $$$$\geqslant\mathrm{3}\:^{\mathrm{3}} \sqrt{\mathrm{m}.\mathrm{y}.\frac{\mathrm{1}}{\mathrm{my}}}=\mathrm{3} \\ $$$$\mathrm{The}\:\mathrm{equality}\:\mathrm{ocurrs}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if} \\ $$$$\mathrm{m}=\mathrm{y}=\frac{\mathrm{1}}{\mathrm{my}}\Leftrightarrow\begin{cases}{\mathrm{m}^{\mathrm{2}} \mathrm{y}=\mathrm{1}}\\{\mathrm{my}^{\mathrm{2}} =\mathrm{1}}\end{cases}\Rightarrow\mathrm{my}=\mathrm{1}\Rightarrow\mathrm{m}=\mathrm{y}=\mathrm{1} \\ $$$$\mathrm{x}=\mathrm{y}+\mathrm{1} \\ $$$$\mathrm{Thus},\mathrm{P}=\mathrm{x}+\frac{\mathrm{1}}{\mathrm{y}\left(\mathrm{x}−\mathrm{y}\right)}\:\mathrm{has}\:\mathrm{smallest} \\ $$$$\mathrm{value}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{3}\:\mathrm{when}\:\mathrm{x}=\mathrm{2},\mathrm{y}=\mathrm{1} \\ $$
