Question Number 110970 by khaki last updated on 01/Sep/20

Commented by khaki last updated on 01/Sep/20
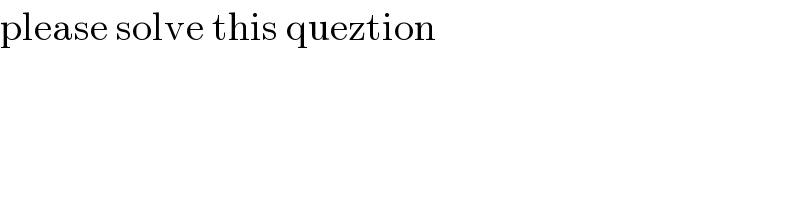
$$\mathrm{please}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{queztion} \\ $$
Answered by mr W last updated on 01/Sep/20
![∫((ax+b)/(ax^2 +bx+c))dx =(1/2)∫((2ax+b+b)/(ax^2 +bx+c))dx =(1/2)[∫((2ax+b)/(ax^2 +bx+c))dx+∫(b/(ax^2 +bx+c))dx] =(1/2)∫((d(ax^2 +bx+c))/(ax^2 +bx+c))+(1/2)∫(b/(ax^2 +bx+c))dx =(1/2)ln ∣ax^2 +bx+c∣+(b/2)∫(1/(ax^2 +bx+c))dx =....](https://www.tinkutara.com/question/Q110983.png)
$$\int\frac{{ax}+{b}}{{ax}^{\mathrm{2}} +{bx}+{c}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{ax}+{b}+{b}}{{ax}^{\mathrm{2}} +{bx}+{c}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\int\frac{\mathrm{2}{ax}+{b}}{{ax}^{\mathrm{2}} +{bx}+{c}}{dx}+\int\frac{{b}}{{ax}^{\mathrm{2}} +{bx}+{c}}{dx}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({ax}^{\mathrm{2}} +{bx}+{c}\right)}{{ax}^{\mathrm{2}} +{bx}+{c}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{b}}{{ax}^{\mathrm{2}} +{bx}+{c}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid{ax}^{\mathrm{2}} +{bx}+{c}\mid+\frac{{b}}{\mathrm{2}}\int\frac{\mathrm{1}}{{ax}^{\mathrm{2}} +{bx}+{c}}{dx} \\ $$$$=…. \\ $$
Commented by mr W last updated on 01/Sep/20

Commented by Her_Majesty last updated on 01/Sep/20

$${what}\:{if}\:{b}^{\mathrm{2}} =\mathrm{4}{ac}? \\ $$
Commented by malwan last updated on 01/Sep/20
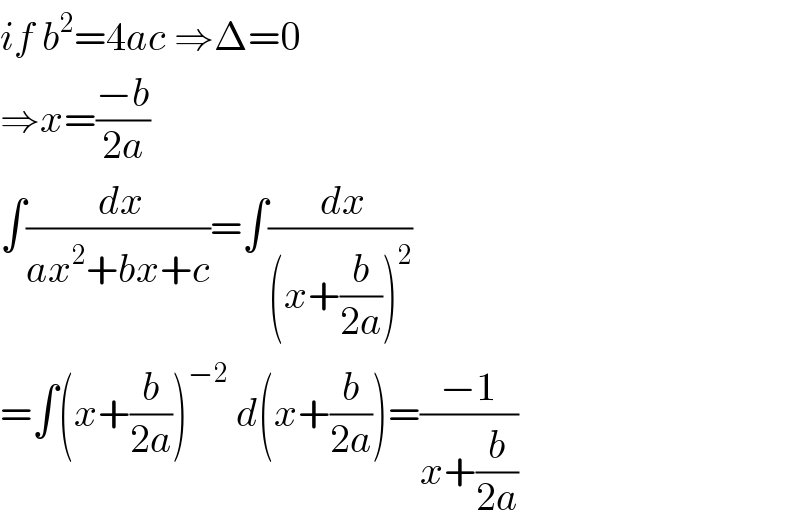
$${if}\:{b}^{\mathrm{2}} =\mathrm{4}{ac}\:\Rightarrow\Delta=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{−{b}}{\mathrm{2}{a}}\:\: \\ $$$$\int\frac{\:{dx}}{{ax}^{\mathrm{2}} +{bx}+{c}}=\int\frac{\:{dx}}{\left({x}+\frac{{b}}{\mathrm{2}{a}}\right)^{\mathrm{2}} } \\ $$$$=\int\left({x}+\frac{{b}}{\mathrm{2}{a}}\right)^{−\mathrm{2}} \:{d}\left({x}+\frac{{b}}{\mathrm{2}{a}}\right)=\frac{−\mathrm{1}}{{x}+\frac{{b}}{\mathrm{2}{a}}} \\ $$
Answered by malwan last updated on 01/Sep/20
![∫(( ax + b)/(ax^2 + bx + c))dx = ∫(( ax +(1/2)b)/(ax^2 + bx + c))dx − (b/2)∫(( dx)/(ax^2 + bx + c)) = (1/2)ln∣ax^2 +bx+c∣−(b/2)I I=∫(( dx)/(a[x^2 +(b/a)x+(c/a)])) =(1/a)∫(( dx)/([(x+(b/(2a)))^2 + ((c/a)−(b^2 /(4a^2 )))])) =(1/a)∫(( dx)/([(((2ax+b)/(2a)))^2 +((4ac−b^2 )/(4a^2 ))])) =(1/a) (1/((4ac−b^2 )/(4a^2 ))) ∫(( dx)/((((2ax+b)^2 )/(4a^2 ))/((4ax−b^2 )/(4a^2 )) +1 )) =((4a)/(4ac−b^2 )) ∫(( dx)/((((2ac+b)/( (√(4ac−b^2 )))))^2 + 1)) t=((2ac)/( (√(4ac−b^2 )))) ⇒dt(√(4ac−b^2 ))=2adx dx=((√(4ac−b^2 ))/(2a)) ∴ I =((4a)/(4ac−b^2 )) ∫((((√(4ac−b^2 ))/(2a)) dt)/(t^2 +1)) =(2/( (√(4ac−b^2 )))) tan^(−1) t + C I= (2/( (√(4ac−b^2 )))) tan^(−1) (((2ax + b)/( (√(4ac −b^2 ))))) + C](https://www.tinkutara.com/question/Q110987.png)
$$\int\frac{\:{ax}\:+\:{b}}{{ax}^{\mathrm{2}} \:+\:{bx}\:+\:{c}}{dx} \\ $$$$=\:\int\frac{\:{ax}\:+\frac{\mathrm{1}}{\mathrm{2}}{b}}{{ax}^{\mathrm{2}} \:+\:{bx}\:+\:{c}}{dx}\:−\:\frac{{b}}{\mathrm{2}}\int\frac{\:{dx}}{{ax}^{\mathrm{2}} \:+\:{bx}\:+\:{c}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{ax}^{\mathrm{2}} +{bx}+{c}\mid−\frac{{b}}{\mathrm{2}}{I} \\ $$$${I}=\int\frac{\:{dx}}{{a}\left[{x}^{\mathrm{2}} +\frac{{b}}{{a}}{x}+\frac{{c}}{{a}}\right]} \\ $$$$=\frac{\mathrm{1}}{{a}}\int\frac{\:{dx}}{\left[\left({x}+\frac{{b}}{\mathrm{2}{a}}\right)^{\mathrm{2}} \:+\:\left(\frac{{c}}{{a}}−\frac{{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\right)\right]} \\ $$$$=\frac{\mathrm{1}}{{a}}\int\frac{\:{dx}}{\left[\left(\frac{\mathrm{2}{ax}+{b}}{\mathrm{2}{a}}\right)^{\mathrm{2}} +\frac{\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\right]} \\ $$$$=\frac{\mathrm{1}}{{a}}\:\frac{\mathrm{1}}{\frac{\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }}\:\int\frac{\:{dx}}{\frac{\left(\mathrm{2}{ax}+{b}\right)^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }/\frac{\mathrm{4}{ax}−{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\:+\mathrm{1}\:} \\ $$$$=\frac{\mathrm{4}{a}}{\mathrm{4}{ac}−{b}^{\mathrm{2}} }\:\int\frac{\:{dx}}{\left(\frac{\mathrm{2}{ac}+{b}}{\:\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}\right)^{\mathrm{2}} \:+\:\mathrm{1}} \\ $$$${t}=\frac{\mathrm{2}{ac}}{\:\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}\:\Rightarrow{dt}\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }=\mathrm{2}{adx} \\ $$$${dx}=\frac{\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}{\mathrm{2}{a}} \\ $$$$\therefore\:{I}\:=\frac{\mathrm{4}{a}}{\mathrm{4}{ac}−{b}^{\mathrm{2}} }\:\int\frac{\frac{\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}{\mathrm{2}{a}}\:{dt}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}\:{tan}^{−\mathrm{1}} \:{t}\:+\:{C} \\ $$$${I}=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}\:{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{ax}\:+\:{b}}{\:\sqrt{\mathrm{4}{ac}\:−{b}^{\mathrm{2}} }}\right)\:+\:{C} \\ $$
Commented by mr W last updated on 01/Sep/20

$${i}\:{think} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{ax}^{\mathrm{2}} +{bx}+{c}\mid+\frac{{b}}{\mathrm{2}}{I} \\ $$
Commented by malwan last updated on 01/Sep/20

$${yes}\:{Sir} \\ $$
