Question-110980

Question Number 110980 by mohammad17 last updated on 01/Sep/20

Commented by mohammad17 last updated on 01/Sep/20

$${help}\:{me}\:{sir} \\ $$

Commented by Her_Majesty last updated on 01/Sep/20

Q5 is wrong. we′re free to choose a,b,c with a≠0. i.e. a=7, b=−7, c=5 ⇒ c is not the midpoint of [7, −7]

$${Q}\mathrm{5}\:{is}\:{wrong}.\:{we}'{re}\:{free}\:{to}\:{choose}\:{a},{b},{c}\:{with} \\ $$$${a}\neq\mathrm{0}.\:{i}.{e}.\:{a}=\mathrm{7},\:{b}=−\mathrm{7},\:{c}=\mathrm{5}\:\Rightarrow\:{c}\:{is}\:{not}\:{the} \\ $$$${midpoint}\:{of}\:\left[\mathrm{7},\:−\mathrm{7}\right] \\ $$

Answered by Her_Majesty last updated on 01/Sep/20

Q3 ∣x∣>0 ⇒ −∣x∣<0 ∀x≠0 ⇒ domain=range=0 Q4 i lim_(x→+∞) ((∣x^2 −4∣)/(2x^2 −3))=lim_(x→+∞) ((x^2 −4)/(2x^2 −3))=(1/2) ii lim_(x→2) ((∣x^2 −4∣)/(x−2)) { ((−2<x<2; −((x^2 −4)/(x−2))=−(((x−2)(x+2))/(x−2))=−(x+2))),((x>2; ((x^2 −4)/(x−2))=(((x−2)(x+2))/(x−2))=x+2)) :} ⇒ lim_(x→2^− ) =−4 ≠ lim_(x→2^+ ) =4 ⇒ lim doesn′t exist

$${Q}\mathrm{3} \\ $$$$\mid{x}\mid>\mathrm{0}\:\Rightarrow\:−\mid{x}\mid<\mathrm{0}\:\forall{x}\neq\mathrm{0} \\ $$$$\Rightarrow\:{domain}={range}=\mathrm{0} \\ $$$${Q}\mathrm{4} \\ $$$${i} \\ $$$${lim}_{{x}\rightarrow+\infty} \frac{\mid{x}^{\mathrm{2}} −\mathrm{4}\mid}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}}={lim}_{{x}\rightarrow+\infty} \frac{{x}^{\mathrm{2}} −\mathrm{4}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${ii} \\ $$$${lim}_{{x}\rightarrow\mathrm{2}} \frac{\mid{x}^{\mathrm{2}} −\mathrm{4}\mid}{{x}−\mathrm{2}}\:\begin{cases}{−\mathrm{2}<{x}<\mathrm{2};\:−\frac{{x}^{\mathrm{2}} −\mathrm{4}}{{x}−\mathrm{2}}=−\frac{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{2}\right)}{{x}−\mathrm{2}}=−\left({x}+\mathrm{2}\right)}\\{{x}>\mathrm{2};\:\frac{{x}^{\mathrm{2}} −\mathrm{4}}{{x}−\mathrm{2}}=\frac{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{2}\right)}{{x}−\mathrm{2}}={x}+\mathrm{2}}\end{cases} \\ $$$$\Rightarrow\:{lim}_{{x}\rightarrow\mathrm{2}^{−} } =−\mathrm{4}\:\neq\:{lim}_{{x}\rightarrow\mathrm{2}^{+} } =\mathrm{4} \\ $$$$\Rightarrow\:{lim}\:{doesn}'{t}\:{exist} \\ $$

Answered by Her_Majesty last updated on 01/Sep/20

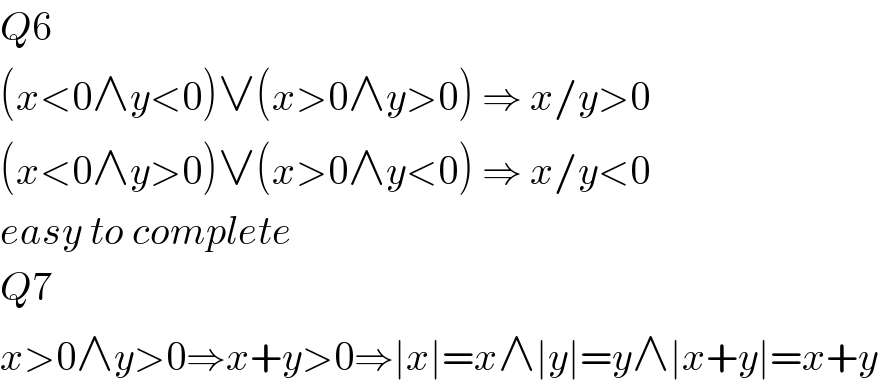
Q6 (x<0∧y<0)∨(x>0∧y>0) ⇒ x/y>0 (x<0∧y>0)∨(x>0∧y<0) ⇒ x/y<0 easy to complete Q7 x>0∧y>0⇒x+y>0⇒∣x∣=x∧∣y∣=y∧∣x+y∣=x+y

$${Q}\mathrm{6} \\ $$$$\left({x}<\mathrm{0}\wedge{y}<\mathrm{0}\right)\vee\left({x}>\mathrm{0}\wedge{y}>\mathrm{0}\right)\:\Rightarrow\:{x}/{y}>\mathrm{0} \\ $$$$\left({x}<\mathrm{0}\wedge{y}>\mathrm{0}\right)\vee\left({x}>\mathrm{0}\wedge{y}<\mathrm{0}\right)\:\Rightarrow\:{x}/{y}<\mathrm{0} \\ $$$${easy}\:{to}\:{complete} \\ $$$${Q}\mathrm{7} \\ $$$${x}>\mathrm{0}\wedge{y}>\mathrm{0}\Rightarrow{x}+{y}>\mathrm{0}\Rightarrow\mid{x}\mid={x}\wedge\mid{y}\mid={y}\wedge\mid{x}+{y}\mid={x}+{y} \\ $$

Commented by mohammad17 last updated on 01/Sep/20

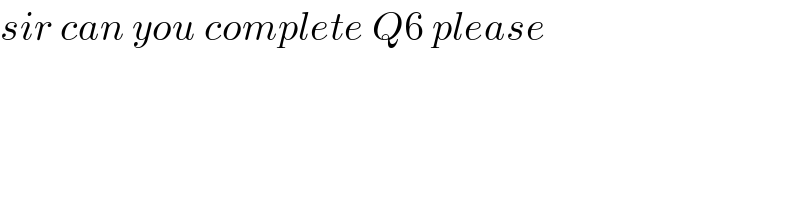
$${sir}\:{can}\:{you}\:{complete}\:{Q}\mathrm{6}\:{please} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply