Question Number 111029 by Khanacademy last updated on 01/Sep/20
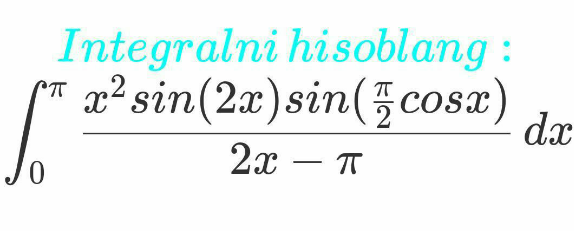
Answered by mindispower last updated on 02/Sep/20
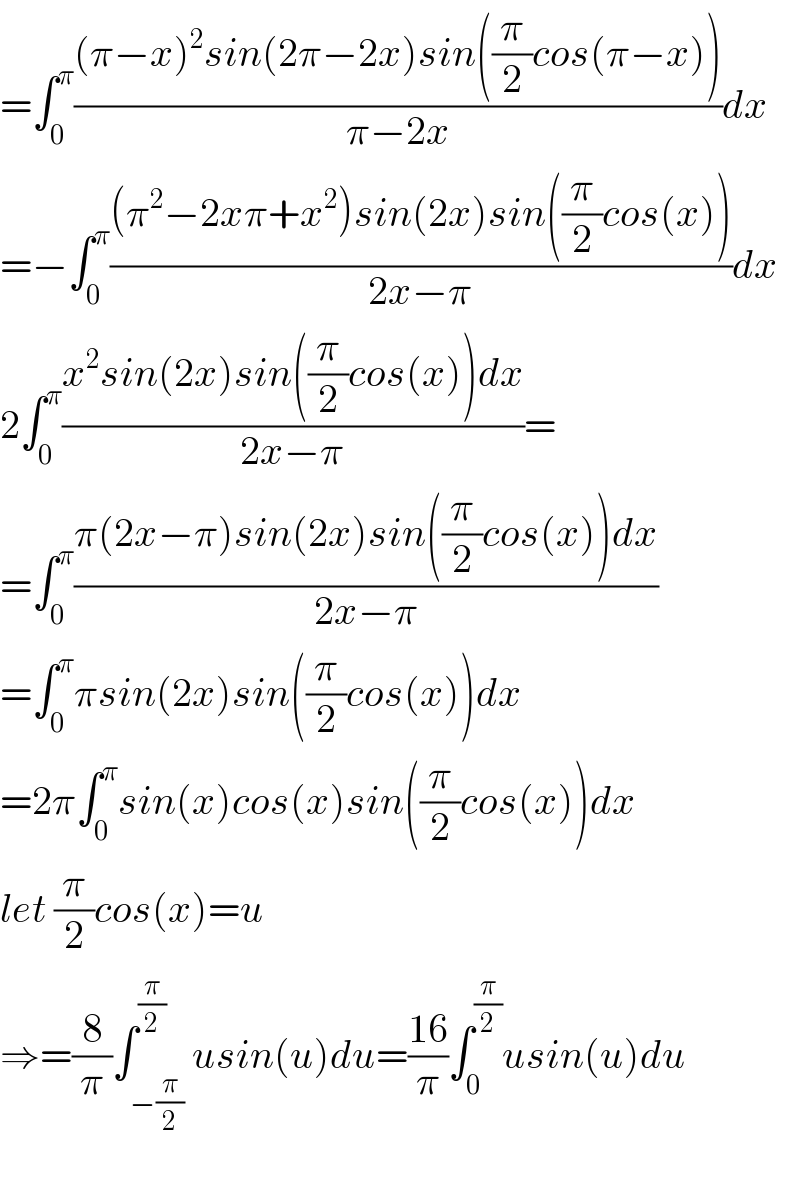
$$=\int_{\mathrm{0}} ^{\pi} \frac{\left(\pi−{x}\right)^{\mathrm{2}} {sin}\left(\mathrm{2}\pi−\mathrm{2}{x}\right){sin}\left(\frac{\pi}{\mathrm{2}}{cos}\left(\pi−{x}\right)\right)}{\pi−\mathrm{2}{x}}{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\pi} \frac{\left(\pi^{\mathrm{2}} −\mathrm{2}{x}\pi+{x}^{\mathrm{2}} \right){sin}\left(\mathrm{2}{x}\right){sin}\left(\frac{\pi}{\mathrm{2}}{cos}\left({x}\right)\right)}{\mathrm{2}{x}−\pi}{dx} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\pi} \frac{{x}^{\mathrm{2}} {sin}\left(\mathrm{2}{x}\right){sin}\left(\frac{\pi}{\mathrm{2}}{cos}\left({x}\right)\right){dx}}{\mathrm{2}{x}−\pi}= \\ $$$$=\int_{\mathrm{0}} ^{\pi} \frac{\pi\left(\mathrm{2}{x}−\pi\right){sin}\left(\mathrm{2}{x}\right){sin}\left(\frac{\pi}{\mathrm{2}}{cos}\left({x}\right)\right){dx}}{\mathrm{2}{x}−\pi} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \pi{sin}\left(\mathrm{2}{x}\right){sin}\left(\frac{\pi}{\mathrm{2}}{cos}\left({x}\right)\right){dx} \\ $$$$=\mathrm{2}\pi\int_{\mathrm{0}} ^{\pi} {sin}\left({x}\right){cos}\left({x}\right){sin}\left(\frac{\pi}{\mathrm{2}}{cos}\left({x}\right)\right){dx} \\ $$$${let}\:\frac{\pi}{\mathrm{2}}{cos}\left({x}\right)={u} \\ $$$$\Rightarrow=\frac{\mathrm{8}}{\pi}\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} {usin}\left({u}\right){du}=\frac{\mathrm{16}}{\pi}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {usin}\left({u}\right){du} \\ $$$$ \\ $$
