Menu Close

Question-111044

Tinku Tara 0 Comments
Pin




Question Number 111044 by mathdave last updated on 01/Sep/20
Commented by kaivan.ahmadi last updated on 01/Sep/20
5. a∣m,b∣m⇒ab∣m on the other hand lcm(a,b)∣ab so lcm(a,b)∣m. 6. let a,b∈R if a=b⇒max(a,b)=min(a,b)=a=b⇒max(a,b)+min(a,b)=a+b=2a=2b if a>b⇒max(a,b)=a,min(a,b)=b⇒ max(a,b)+min(a,b)=a+b.
$$\mathrm{5}. \\ $$$${a}\mid{m},{b}\mid{m}\Rightarrow{ab}\mid{m}\:{on}\:{the}\:{other}\:{hand} \\ $$$${lcm}\left({a},{b}\right)\mid{ab}\:{so}\:{lcm}\left({a},{b}\right)\mid{m}. \\ $$$$\mathrm{6}. \\ $$$${let}\:{a},{b}\in\mathbb{R} \\ $$$${if}\:{a}={b}\Rightarrow{max}\left({a},{b}\right)={min}\left({a},{b}\right)={a}={b}\Rightarrow{max}\left({a},{b}\right)+{min}\left({a},{b}\right)={a}+{b}=\mathrm{2}{a}=\mathrm{2}{b} \\ $$$${if}\:{a}>{b}\Rightarrow{max}\left({a},{b}\right)={a},{min}\left({a},{b}\right)={b}\Rightarrow \\ $$$${max}\left({a},{b}\right)+{min}\left({a},{b}\right)={a}+{b}. \\ $$$$ \\ $$$$ \\ $$
Commented by kaivan.ahmadi last updated on 02/Sep/20
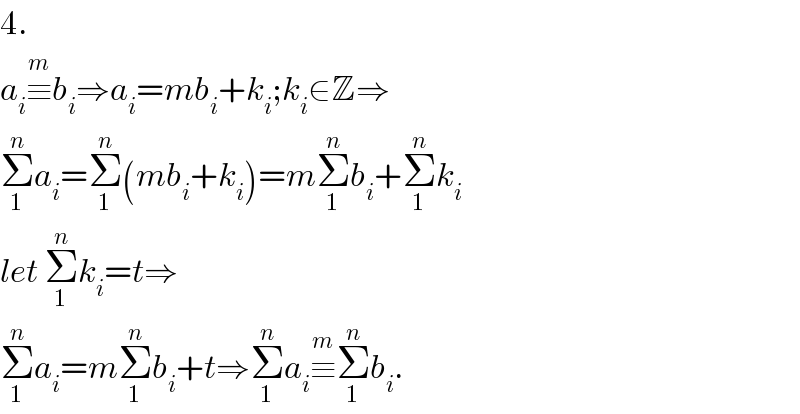
4. a_i ≡^m b_i ⇒a_i =mb_i +k_i ;k_i ∈Z⇒ Σ_1 ^n a_i =Σ_1 ^n (mb_i +k_i )=mΣ_1 ^n b_i +Σ_1 ^n k_i let Σ_1 ^n k_i =t⇒ Σ_1 ^n a_i =mΣ_1 ^n b_i +t⇒Σ_1 ^n a_i ≡^m Σ_1 ^n b_i .
$$\mathrm{4}. \\ $$$${a}_{{i}} \overset{{m}} {\equiv}{b}_{{i}} \Rightarrow{a}_{{i}} ={mb}_{{i}} +{k}_{{i}} ;{k}_{{i}} \in\mathbb{Z}\Rightarrow \\ $$$$\underset{\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} =\underset{\mathrm{1}} {\overset{{n}} {\sum}}\left({mb}_{{i}} +{k}_{{i}} \right)={m}\underset{\mathrm{1}} {\overset{{n}} {\sum}}{b}_{{i}} +\underset{\mathrm{1}} {\overset{{n}} {\sum}}{k}_{{i}} \\ $$$${let}\:\underset{\mathrm{1}} {\overset{{n}} {\sum}}{k}_{{i}} ={t}\Rightarrow \\ $$$$\underset{\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} ={m}\underset{\mathrm{1}} {\overset{{n}} {\sum}}{b}_{{i}} +{t}\Rightarrow\underset{\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} \overset{{m}} {\equiv}\underset{\mathrm{1}} {\overset{{n}} {\sum}}{b}_{{i}} . \\ $$
Commented by kaivan.ahmadi last updated on 01/Sep/20
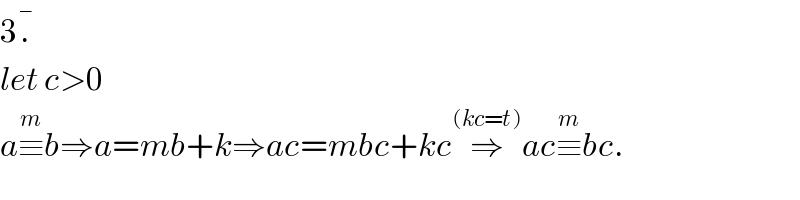
3.^� let c>0 a≡^m b⇒a=mb+k⇒ac=mbc+kc⇒^((kc=t)) ac≡^m bc.
$$\mathrm{3}\bar {.} \\ $$$${let}\:{c}>\mathrm{0} \\ $$$${a}\overset{{m}} {\equiv}{b}\Rightarrow{a}={mb}+{k}\Rightarrow{ac}={mbc}+{kc}\overset{\left({kc}={t}\right)} {\Rightarrow}{ac}\overset{{m}} {\equiv}{bc}. \\ $$
Commented by kaivan.ahmadi last updated on 01/Sep/20
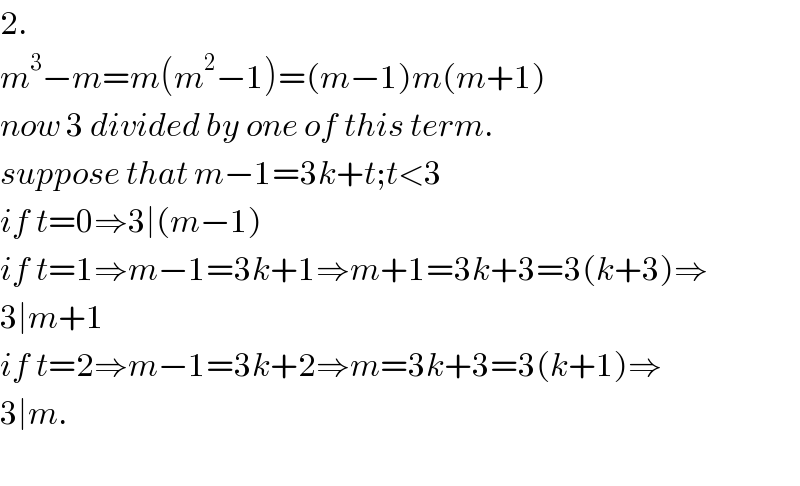
2. m^3 −m=m(m^2 −1)=(m−1)m(m+1) now 3 divided by one of this term. suppose that m−1=3k+t;t<3 if t=0⇒3∣(m−1) if t=1⇒m−1=3k+1⇒m+1=3k+3=3(k+3)⇒ 3∣m+1 if t=2⇒m−1=3k+2⇒m=3k+3=3(k+1)⇒ 3∣m.
$$\mathrm{2}. \\ $$$${m}^{\mathrm{3}} −{m}={m}\left({m}^{\mathrm{2}} −\mathrm{1}\right)=\left({m}−\mathrm{1}\right){m}\left({m}+\mathrm{1}\right) \\ $$$${now}\:\mathrm{3}\:{divided}\:{by}\:{one}\:{of}\:{this}\:{term}. \\ $$$${suppose}\:{that}\:{m}−\mathrm{1}=\mathrm{3}{k}+{t};{t}<\mathrm{3} \\ $$$${if}\:{t}=\mathrm{0}\Rightarrow\mathrm{3}\mid\left({m}−\mathrm{1}\right) \\ $$$${if}\:{t}=\mathrm{1}\Rightarrow{m}−\mathrm{1}=\mathrm{3}{k}+\mathrm{1}\Rightarrow{m}+\mathrm{1}=\mathrm{3}{k}+\mathrm{3}=\mathrm{3}\left({k}+\mathrm{3}\right)\Rightarrow \\ $$$$\mathrm{3}\mid{m}+\mathrm{1} \\ $$$${if}\:{t}=\mathrm{2}\Rightarrow{m}−\mathrm{1}=\mathrm{3}{k}+\mathrm{2}\Rightarrow{m}=\mathrm{3}{k}+\mathrm{3}=\mathrm{3}\left({k}+\mathrm{1}\right)\Rightarrow \\ $$$$\mathrm{3}\mid{m}. \\ $$$$ \\ $$
Answered by Rio Michael last updated on 02/Sep/20
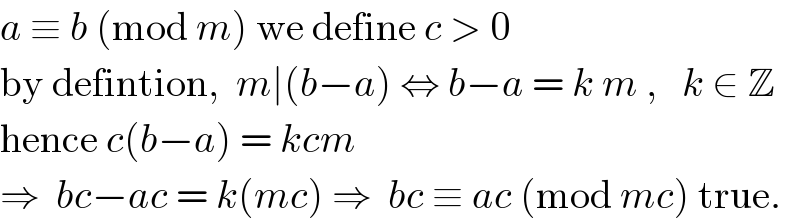
a ≡ b (mod m) we define c > 0 by defintion, m∣(b−a) ⇔ b−a = k m , k ∈ Z hence c(b−a) = kcm ⇒ bc−ac = k(mc) ⇒ bc ≡ ac (mod mc) true.
$${a}\:\equiv\:{b}\:\left(\mathrm{mod}\:{m}\right)\:\mathrm{we}\:\mathrm{define}\:{c}\:>\:\mathrm{0} \\ $$$$\mathrm{by}\:\mathrm{defintion},\:\:{m}\mid\left({b}−{a}\right)\:\Leftrightarrow\:{b}−{a}\:=\:{k}\:{m}\:,\:\:\:{k}\:\in\:\mathbb{Z} \\ $$$$\mathrm{hence}\:{c}\left({b}−{a}\right)\:=\:{kcm}\: \\ $$$$\Rightarrow\:\:{bc}−{ac}\:=\:{k}\left({mc}\right)\:\Rightarrow\:\:{bc}\:\equiv\:{ac}\:\left(\mathrm{mod}\:{mc}\right)\:\mathrm{true}.\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *