Question Number 111067 by Algoritm last updated on 01/Sep/20
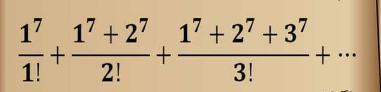
Commented by Her_Majesty last updated on 01/Sep/20
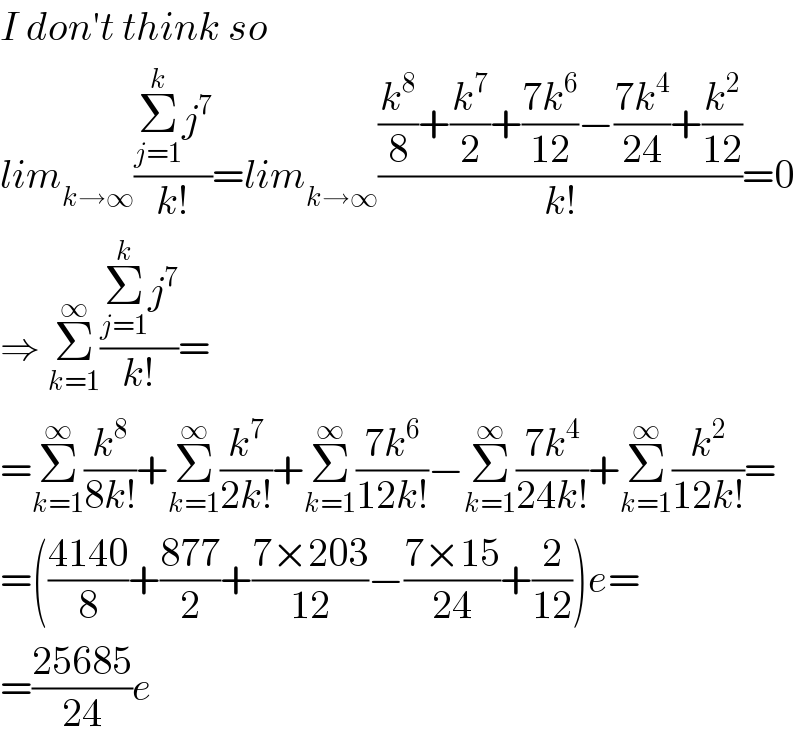
$${I}\:{don}'{t}\:{think}\:{so} \\ $$$${lim}_{{k}\rightarrow\infty} \frac{\underset{{j}=\mathrm{1}} {\overset{{k}} {\sum}}{j}^{\mathrm{7}} }{{k}!}={lim}_{{k}\rightarrow\infty} \frac{\frac{{k}^{\mathrm{8}} }{\mathrm{8}}+\frac{{k}^{\mathrm{7}} }{\mathrm{2}}+\frac{\mathrm{7}{k}^{\mathrm{6}} }{\mathrm{12}}−\frac{\mathrm{7}{k}^{\mathrm{4}} }{\mathrm{24}}+\frac{{k}^{\mathrm{2}} }{\mathrm{12}}}{{k}!}=\mathrm{0} \\ $$$$\Rightarrow\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\underset{{j}=\mathrm{1}} {\overset{{k}} {\sum}}{j}^{\mathrm{7}} }{{k}!}= \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}^{\mathrm{8}} }{\mathrm{8}{k}!}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}^{\mathrm{7}} }{\mathrm{2}{k}!}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{7}{k}^{\mathrm{6}} }{\mathrm{12}{k}!}−\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{7}{k}^{\mathrm{4}} }{\mathrm{24}{k}!}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}^{\mathrm{2}} }{\mathrm{12}{k}!}= \\ $$$$=\left(\frac{\mathrm{4140}}{\mathrm{8}}+\frac{\mathrm{877}}{\mathrm{2}}+\frac{\mathrm{7}×\mathrm{203}}{\mathrm{12}}−\frac{\mathrm{7}×\mathrm{15}}{\mathrm{24}}+\frac{\mathrm{2}}{\mathrm{12}}\right){e}= \\ $$$$=\frac{\mathrm{25685}}{\mathrm{24}}{e} \\ $$
Commented by Algoritm last updated on 02/Sep/20

$$\mathrm{thanks} \\ $$
