Question Number 111125 by bemath last updated on 02/Sep/20
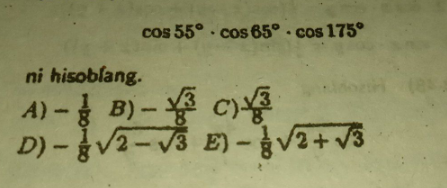
Answered by Dwaipayan Shikari last updated on 02/Sep/20
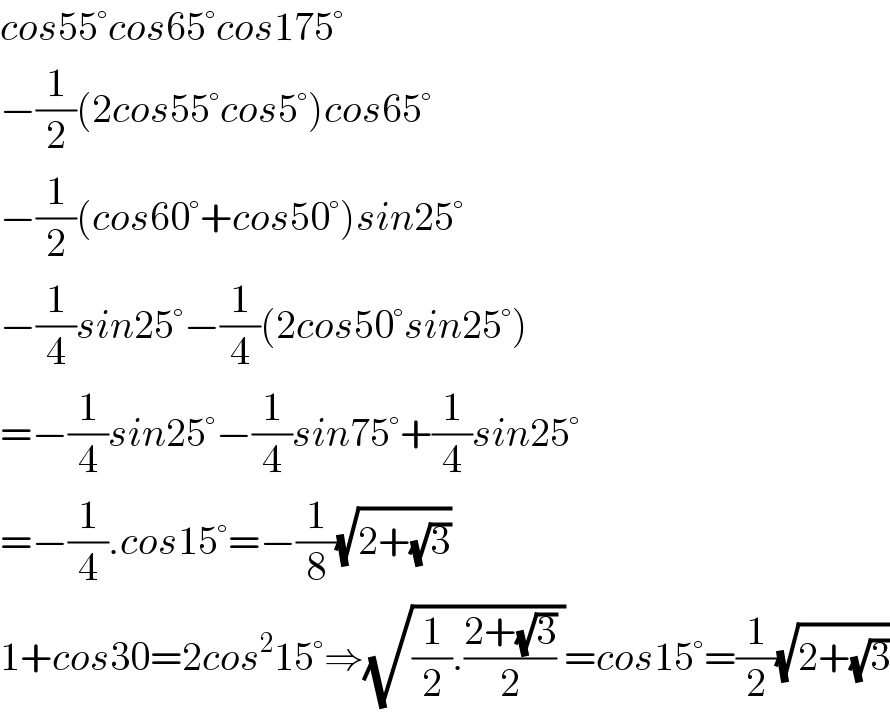
$${cos}\mathrm{55}°{cos}\mathrm{65}°{cos}\mathrm{175}° \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{cos}\mathrm{55}°{cos}\mathrm{5}°\right){cos}\mathrm{65}° \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\mathrm{60}°+{cos}\mathrm{50}°\right){sin}\mathrm{25}° \\ $$$$−\frac{\mathrm{1}}{\mathrm{4}}{sin}\mathrm{25}°−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}{cos}\mathrm{50}°{sin}\mathrm{25}°\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}{sin}\mathrm{25}°−\frac{\mathrm{1}}{\mathrm{4}}{sin}\mathrm{75}°+\frac{\mathrm{1}}{\mathrm{4}}{sin}\mathrm{25}° \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}.{cos}\mathrm{15}°=−\frac{\mathrm{1}}{\mathrm{8}}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$$\mathrm{1}+{cos}\mathrm{30}=\mathrm{2}{cos}^{\mathrm{2}} \mathrm{15}°\Rightarrow\sqrt{\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{2}}\:}={cos}\mathrm{15}°=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$
